Как сделать линию кривой через точки

Я ищу способ сделать линию кривой через ряд точек. Было бы предпочтительнее использовать 3 точки, хотя я считал, что для того, чтобы дать контекст углу линии, входящей в точку, может потребоваться больше, чтобы, так сказать, задать контекст кривой.

В общем, начальная точка P1, контрольная точка P2 и конечная точка P3, линия должна изгибаться до P2 от P1, а затем изгибаться от P2 до P3.

Фактически, вот прекрасный пример эффекта, которого я хотел бы достичь:

Ирвин Холл Сплайн

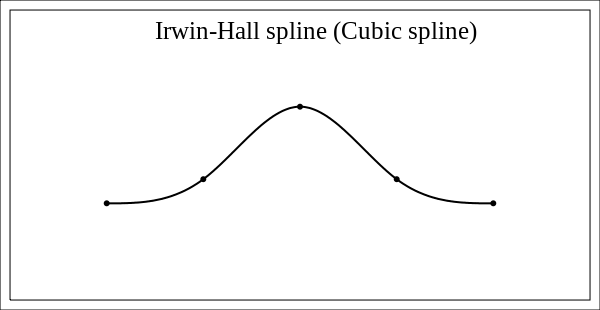
Если бы я мог сделать это, я был бы вечно благодарен!

До сих пор в Java я пытался поиграть с такими вещами, как QuadCurve2D.Double, Cub icCurve2D.Double, а также Path2D.Double (с использованием curveTo с Path2D.Double), но безрезультатно - кривые, которые нарисованы, даже не близки проходить через указанную контрольную точку.

Вот изображение методов, которые я пробовал до сих пор:

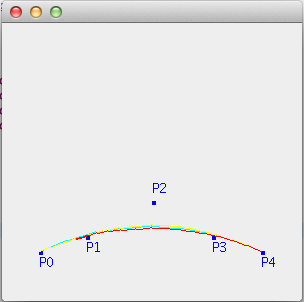
А вот код, который я использовал для генерации точек и кривых на изображении:

    Graphics2D g = (Graphics2D) window.getGraphics();
    g.setColor(Color.blue);
    int d = 4;

    // P0
    int x0 = window.getWidth()/8;
    int y0 = 250;
    g.drawString("P0", x0, y0 + 4*d);
    g.fillRect(x0, y0, d, d);

    // P1
    int x1 = (window.getWidth()/7)*2;
    int y1 = 235;
    g.drawString("P1", x1, y1 + 4*d);
    g.fillRect(x1, y1, d, d);

    // P2
    int x2 = (window.getWidth()/2);
    int y2 = 200;
    g.drawString("P2", x2, y2 - 2*d);
    g.fillRect(x2, y2, d, d);

    // P3
    int x3 = (window.getWidth()/7)*5;
    int y3 = 235;
    g.drawString("P3", x3, y3 + 4*d);
    g.fillRect(x3, y3, d, d);

            // P4
    int x4 = (window.getWidth()/8)*7;
    int y4 = 250;
    g.drawString("P4", x4, y4 + 4*d);
    g.fillRect(x4, y4, d, d);

    g.setColor(Color.cyan);
    QuadCurve2D quadCurve = new QuadCurve2D.Double(x0, y0, x2, y2, x4, y4);
    g.draw(quadCurve);


    g.setColor(Color.YELLOW);
    CubicCurve2D.Double cubicCurve = new CubicCurve2D.Double((double)x0, (double)y0, 
                                                             (double)x1, (double)y1, 
                                                             (double)x2, (double)y2, 
                                                             (double)x4, (double)y4);
    g.draw(cubicCurve);


    g.setColor(Color.red);      
    Path2D.Double path1 = new Path2D.Double();
    path1.moveTo(x1, y1);
    path1.curveTo(x0, y0, x2, y2, x4, y4);
    g.draw(path1);

Мои причины для того, чтобы кривая линия проходила через точки, состоит в том, что я хочу "сгладить" переход между вершинами на линейном графике, который я написал. Прежде чем кто-либо упомянет это, JFree Chart не вариант. Я понимаю, что используются разные типы кривых и сплайнов, но мне не очень повезло, чтобы понять, как именно они работают или как реализовать то, что соответствует моим потребностям.

Буду очень признателен за любую предложенную помощь - заранее спасибо.

Источник

3 ответа

Решение

Я думаю, что вам не хватает представления о том, что такое контрольная точка. Контрольные точки, как правило, не на самом пути. Вместо этого они контролируют, как кривая пути формируется между точками. См. Учебник по сплайну для получения полной информации.

Теперь к проблеме, у вас есть точки на кривой, но нет реальных контрольных точек. Есть несколько методов, таких как Cardinal Spline, для получения контрольных точек, которые затем передаются в один из API-интерфейсов рисования кривых, которые вы упомянули. Вы, вероятно, хотите Path2D.Double вариант, так что вы можете плавно объединить отдельные кривые.

Таким образом, для рисования от P1 до P2 в P3, а не

Path2D.Double path1 = new Path2D.Double();
path1.moveTo(x1, y1);
path1.curveTo(x0, y0, x2, y2, x4, y4);
g.draw(path1);

Ты хочешь

Path2D.Double path1 = new Path2D.Double();
path1.moveTo(x1, y1);
path1.curveTo(cx1a, cy1a, cx1b, cy1b, x2, y2);
path1.curveTo(cx2a, cy2a, cx2b, cy2b, x3, y3);
g.draw(path1);

где cx а также cy координаты - это ваши производные контрольные точки, две контрольные точки на сегмент кубического сплайна. Возможно,

cx1a = x1 + (x2 - x1) / 3;
cy1a = y1 + (y2 - y1) / 3;
cx1b = x2 - (x3 - x1) / 3;
cy1b = y2 - (y3 - y1) / 3;
cx2a = x2 + (x3 - x1) / 3;
cy2a = y2 + (y3 - y1) / 3;
cx2b = x3 - (x3 - x2) / 3;
cy2b = y3 - (y3 - y2) / 3;

Шаблон здесь таков, что для внутренних точек (в данном случае только P2) контрольные точки до и после нее (c1b и c2a) смещены на наклон линии между точками до и после нее (P1 и P3). Для краевых точек контрольные точки основаны на наклоне между этой точкой и следующей ближайшей точкой.

Если у вас есть информация о конкретном домене, вы можете выбрать другие контрольные точки. Например, вы можете захотеть, чтобы уклоны в конечных точках были равны 0.

Источник

В основном вы запрашиваете кубическую сплайн-интерполяцию, я смог найти эту программу онлайн Interp2.java, Это фактически включает полиномиальный сплайн и кубический сплайн.

К сожалению, это апплет, а не реальный класс, но вы все еще можете просмотреть код и узнать, как они это сделали. Что всегда хорошо.

Источник

Ну может это поможет:P

Кривые Катмулла-Рома на примере одних и тех же принципов различаются по языку... http://schepers.cc/svg/path/dotty.svg

Источник
Другие вопросы по тегам