Есть ли эквивалент для scipy.signal.deconvolve для 2D-массивов?

Question

Я хотел бы деконвертировать 2D-изображение с помощью функции рассеяния точки (PSF). Я видел, что есть scipy.signal.deconvolve функция, которая работает для одномерных массивов, и scipy.signal.fftconvolve сворачивать многомерные массивы. Есть ли в scipy определенная функция для деконверсии 2D-массивов?

Я определил функцию fftdeconvolve, заменив продукт в fftconvolve делением:

def fftdeconvolve(in1, in2, mode="full"):
    """Deconvolve two N-dimensional arrays using FFT. See convolve.

    """
    s1 = np.array(in1.shape)
    s2 = np.array(in2.shape)
    complex_result = (np.issubdtype(in1.dtype, np.complex) or
                      np.issubdtype(in2.dtype, np.complex))
    size = s1+s2-1

    # Always use 2**n-sized FFT
    fsize = 2**np.ceil(np.log2(size))
    IN1 = fftpack.fftn(in1,fsize)
    IN1 /= fftpack.fftn(in2,fsize)
    fslice = tuple([slice(0, int(sz)) for sz in size])
    ret = fftpack.ifftn(IN1)[fslice].copy()
    del IN1
    if not complex_result:
        ret = ret.real
    if mode == "full":
        return ret
    elif mode == "same":
        if np.product(s1,axis=0) > np.product(s2,axis=0):
            osize = s1
        else:
            osize = s2
        return _centered(ret,osize)
    elif mode == "valid":
        return _centered(ret,abs(s2-s1)+1)

Однако приведенный ниже код не восстанавливает исходный сигнал после свертки и развёртки:

sx, sy = 100, 100
X, Y = np.ogrid[0:sx, 0:sy]
star = stats.norm.pdf(np.sqrt((X - sx/2)**2 + (Y - sy/2)**2), 0, 4)
psf = stats.norm.pdf(np.sqrt((X - sx/2)**2 + (Y - sy/2)**2), 0, 10)

star_conv = fftconvolve(star, psf, mode="same")
star_deconv = fftdeconvolve(star_conv, psf, mode="same")

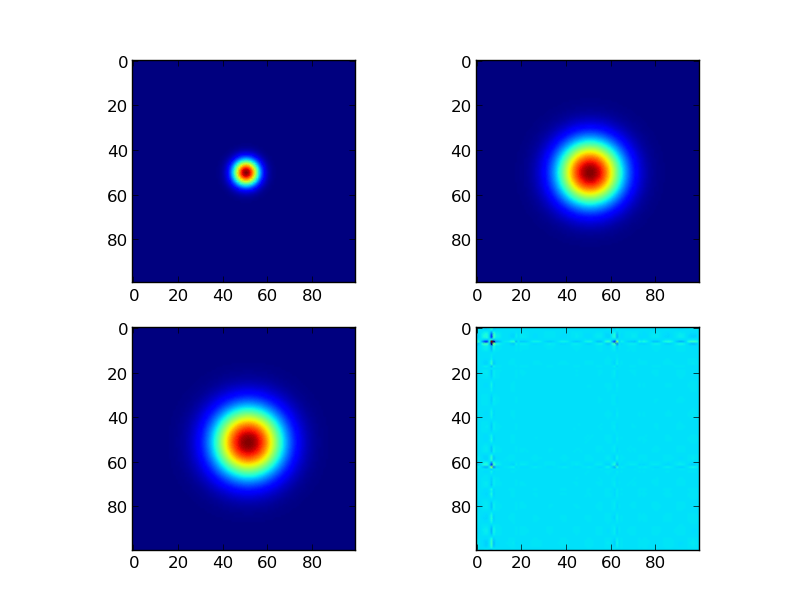
f, axes = plt.subplots(2,2)
axes[0,0].imshow(star)
axes[0,1].imshow(psf)
axes[1,0].imshow(star_conv)
axes[1,1].imshow(star_deconv)
plt.show()

Результирующие двумерные массивы показаны в нижнем ряду на рисунке ниже. Как я могу восстановить исходный сигнал, используя деконволюцию FFT?

Answer 1

Эти функции, использующие fftn, ifftn, fftshift и ifftshift из пакета SciPy's fftpack, похоже, работают:

from scipy import fftpack

def convolve(star, psf):
    star_fft = fftpack.fftshift(fftpack.fftn(star))
    psf_fft = fftpack.fftshift(fftpack.fftn(psf))
    return fftpack.fftshift(fftpack.ifftn(fftpack.ifftshift(star_fft*psf_fft)))

def deconvolve(star, psf):
    star_fft = fftpack.fftshift(fftpack.fftn(star))
    psf_fft = fftpack.fftshift(fftpack.fftn(psf))
    return fftpack.fftshift(fftpack.ifftn(fftpack.ifftshift(star_fft/psf_fft)))

star_conv = convolve(star, psf)
star_deconv = deconvolve(star_conv, psf)

f, axes = plt.subplots(2,2)
axes[0,0].imshow(star)
axes[0,1].imshow(psf)
axes[1,0].imshow(np.real(star_conv))
axes[1,1].imshow(np.real(star_deconv))
plt.show()

Изображение слева внизу показывает свертку двух гауссовских функций в верхнем ряду, а обратный эффект свертки показан в правом нижнем углу.

Answer 2

Обратите внимание, что деконволюция делением в области Фурье не очень полезна ни для чего, кроме демонстрационных целей; любой шум, даже численный, может сделать ваш результат совершенно непригодным для использования. Можно регулировать шум различными способами; но по моему опыту, итерация RL проще в реализации и во многих отношениях более физически оправдана.