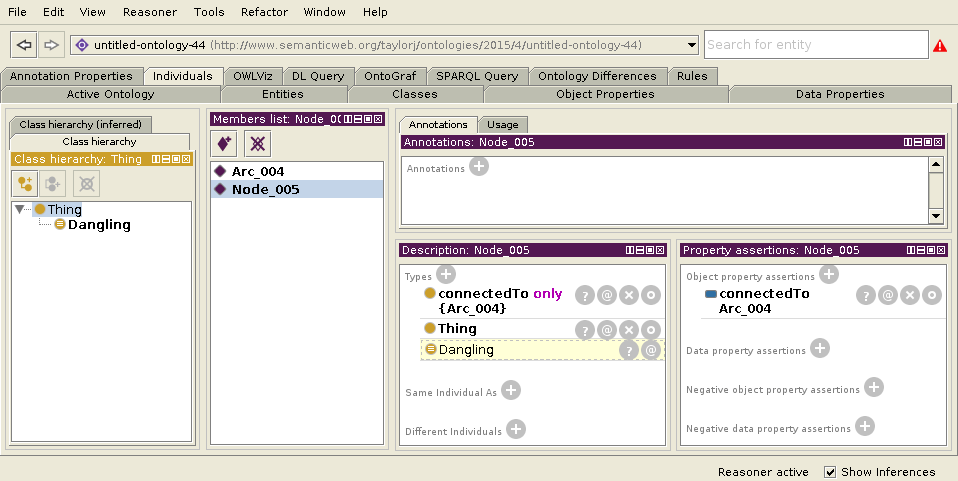
Аксиома замыкания для экземпляров, чтобы рассудитель мог правильно классифицировать экземпляры в онтологии

Question

Я географ и новичок в области онтологии, пытающийся разобраться в этих двух. Поэтому я создал простую онтологию:

Thing
    Feature
        Lane
        Segment(equivalent to Arc)
    Geometry
        Arc (equivalent to Segment)
        Node
            Dangling_Node
            Intersection_node

вы можете найти .owl file здесь создается экземпляр с очень простым пространственным набором данных дороги (рис. 1).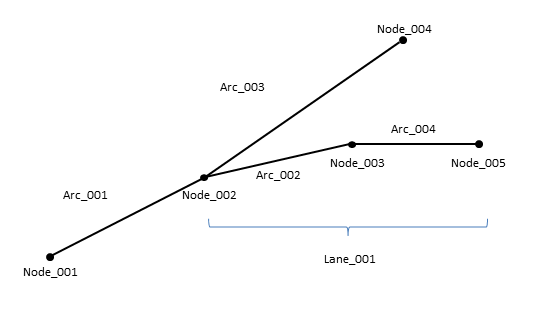

онтология согласована как с экземплярами, так и с экземплярами, но когда я запускаю генератор, экземпляры Dangling_node (узлы, которые связаны с одной ссылкой или дугой) неправильно назначаются соответствующему подклассу и назначаются только суперклассу Node. Экземпляры intersection_node (узел, который связан с несколькими ссылками) правильно назначены.

Я предполагаю, что согласно предположению открытого мира, рассудитель считает, что узел может быть "is_extent_of" другой дуги, но просто не упомянут здесь.

Нужна ли мне, или как я мог, аксиома закрытия для данного случая? Какая часть моей реализации онтологии неверна?

Отредактировано:

Equivalent to:
    Node and (is_extent_of max 1 Arc)
Subclass of (Anonymous Ancester):
    (is_extent_of only Arc) and (is_extent_of min 1 Arc)

аксиома общего класса для Dangling_node выглядит следующим образом:

Node and (is_extent_of max 1 Arc) SubClassOf Dangling_node

Answer 1

экземпляры Dangling_node (узлы, которые связаны с одной ссылкой или дугой) назначены неправильно

Вы должны были бы утверждать, что это правда, а затем то, что не правда. Например, поскольку Node_005 подключен только к Arc_004, вам нужно будет сказать что-то вроде этого:

(1) подключено (Node_005,Arc_004)

а также

(2)        {Node_005} ⊑ neconnectedTo. {Arc_004}

(1) говорит, что узел на самом деле связан с дугой. (2) говорит, что все, к чему подключен узел, является элементом класса {Arc_004}, то есть единственное, к чему он подключен, - это та дуга. Затем вы получите аксиому, которая гласит, что если что-то связано не более чем с одной дугой, то это висячий узел:

(3) (≤ connectedTo.1) ⊑ DanglingNode

(3) является аксиомой общего класса. Вы можете ввести их в Protege, но пользовательский интерфейс не делает это очевидным. Смотрите этот ответ для получения дополнительной информации о том, как их создать.

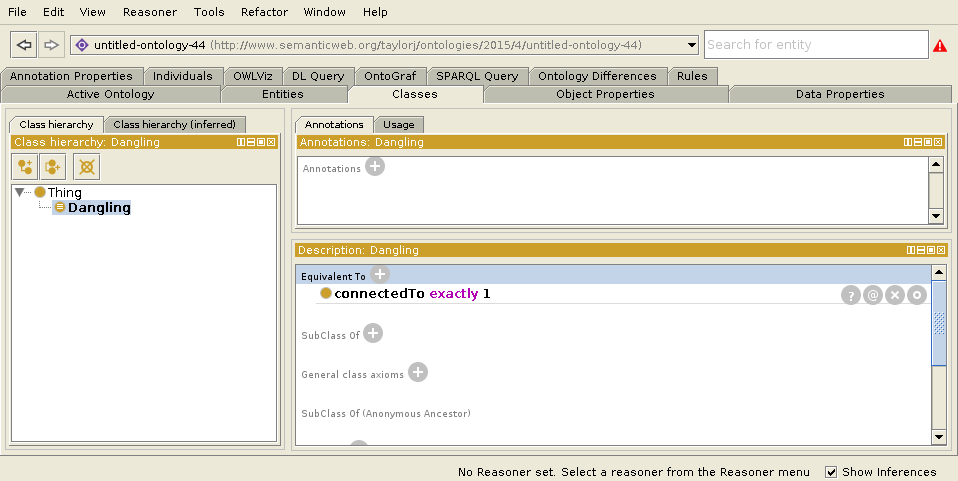
Вот как это выглядит в Protege (за исключением того, что вместо аксиомы общего класса (3) я просто сделал Dangling эквивалентным connectedTo ровно 1):

Определение класса для Dangling

Аксиомы об Узле

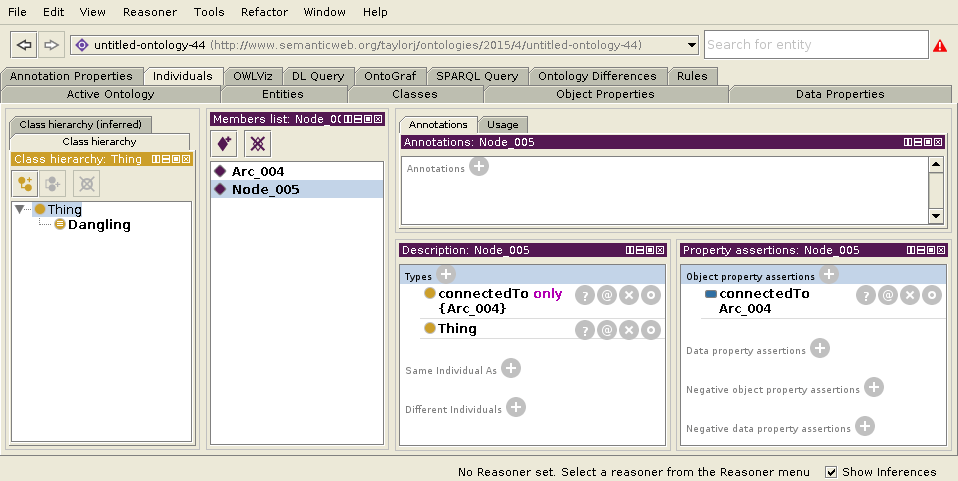
Результат Разумника (Узел Оборван)