SIFT Taylor Expansion разрабатывает субпиксельные локации

Question

Я пытаюсь реализовать SIFT и в настоящее время просто пытаюсь понять, как он работает, прежде чем приступить к его реализации в MATLAB, я понимаю большинство из них, за исключением того, как определить субпиксельную точность с использованием расширения Тейлора:

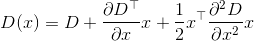
Выше приведено уравнение из оригинальной статьи. У меня есть несколько вопросов о том, как это применяется.

Разрабатываются ли производные в каждом измерении отдельно, а затем уравнение применяется к x, а затем к y?

Применяются ли первый и второй производные вдоль оси сигмы?

Я устал смотреть на предыдущие реализации, но не могу найти, где они это делают. заранее спасибо

Answer 1

В нашем случае D - это объемная функция с переменными x = (x, y, s), где s - масштаб в октаве.

Вопрос: Производны ли производные в каждом измерении отдельно, а затем уравнение применяется к x и y?

Ответ: "Производные разрабатываются в каждом измерении отдельно?" Да, для первой производной мы вычисляем частные производные для x, y и s отдельно. "уравнение применяется к x, то y?", нет, результатом частных производных будет вектор длины 3, который мы просто умножим на обратный гессиан (матрица 3 X 3), чтобы вычислить положение субпикселя x.

Для второй производной мы используем гессианову матрицу (в данном случае матрица 3X3).

Вопрос: Применяются ли первый и второй производные вдоль оси сигмы?

Ответьте Да, потому что это представляет ось в трехмерном пространстве, где D определен.

Заметки:

• Для математически разработанного объяснения см.
• Для кода в C++ см.
• Чтобы вычислить частную производную в дискретной области, мы используем конечные разности.