Является ли целочисленное вычитание без знака определенным поведением?
Я сталкивался с кодом от кого-то, кто, кажется, полагает, что есть проблема вычитания целого числа без знака из другого целого числа того же типа, когда результат будет отрицательным. Так что такой код будет неправильным, даже если он работает на большинстве архитектур.
unsigned int To, Tf;
To = getcounter();
while (1) {
Tf = getcounter();
if ((Tf-To) >= TIME_LIMIT) {
break;
}
}
Это единственная неопределенная цитата из стандарта Си, которую я смог найти.
Вычисления с использованием беззнаковых операндов никогда не могут переполниться, потому что результат, который не может быть представлен результирующим целочисленным типом без знака, уменьшается по модулю на число, которое на единицу больше наибольшего значения, которое может быть представлено результирующим типом.
Я полагаю, что можно принять эту цитату, чтобы обозначить, что когда правый операнд больше, операция корректируется, чтобы иметь смысл в контексте усеченных по модулю чисел.
т.е.
0x0000 - 0x0001 == 0x 1 0000 - 0x0001 == 0xFFFF
в отличие от использования зависимой от реализации подписанной семантики:
0x0000 - 0x0001 == (без знака)(0 + -1) == (0xFFFF, но также 0xFFFE или 0x8001)
Какая или какая интерпретация правильная? Это определено вообще?
6 ответов
Результат вычитания, генерирующего отрицательное число в типе без знака, хорошо определен:
- [...] Вычисление с использованием беззнаковых операндов никогда не может быть переполнено, поскольку результат, который не может быть представлен результирующим целочисленным типом без знака, уменьшается по модулю на число, которое на единицу больше, чем наибольшее значение, которое может быть представлено результирующим типом. (ISO/IEC 9899:1999 (E) §6.2.5/9)
Как вы видете, (unsigned)0 - (unsigned)1 равно -1 по модулю UINT_MAX+1 или, другими словами, UINT_MAX.
Обратите внимание, что хотя в нем говорится: "Вычисление с использованием беззнаковых операндов никогда не может переполниться", что может заставить вас поверить, что оно применимо только для превышения верхнего предела, это представляется как мотивация для действительной обязательной части предложения: "a результат, который не может быть представлен результирующим целочисленным типом без знака, уменьшается по модулю на число, которое на единицу больше наибольшего значения, которое может быть представлено результирующим типом." Эта фраза не ограничена переполнением верхней границы типа и применяется в равной степени к значениям, слишком низким для представления.
Когда вы работаете с неподписанными типами, имеет место модульная арифметика (также известная как поведение "обтекания"). Чтобы понять эту модульную арифметику, просто взгляните на эти часы:
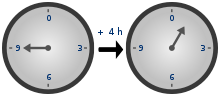
9 + 4 = 1 (13 мод 12), поэтому в другом направлении это: 1 - 4 = 9 (-3 мод 12). Тот же принцип применяется при работе с неподписанными типами. Если тип результата unsigned, тогда имеет место модульная арифметика.
Теперь посмотрите на следующие операции, сохраняющие результат как unsigned int:
unsigned int five = 5, seven = 7;
unsigned int a = five - seven; // a = (-2 % 2^32) = 4294967294
int one = 1, six = 6;
unsigned int b = one - six; // b = (-5 % 2^32) = 4294967291
Когда вы хотите убедиться, что результат signed, а затем сохранил его в signed переменная или приведение к signed, Если вы хотите получить разницу между числами и убедиться, что модульная арифметика не будет применена, то вам следует рассмотреть возможность использования abs() функция, определенная в stdlib.h:
int c = five - seven; // c = -2
int d = abs(five - seven); // d = 2
Будьте очень осторожны, особенно при написании условий, потому что:
if (abs(five - seven) < seven) // = if (2 < 7)
// ...
if (five - seven < -1) // = if (-2 < -1)
// ...
if (one - six < 1) // = if (-5 < 1)
// ...
if ((int)(five - seven) < 1) // = if (-2 < 1)
// ...
но
if (five - seven < 1) // = if ((unsigned int)-2 < 1) = if (4294967294 < 1)
// ...
if (one - six < five) // = if ((unsigned int)-5 < 5) = if (4294967291 < 5)
// ...
Ну, первое толкование верно. Однако ваши рассуждения о "подписанной семантике" в этом контексте неверны.
Опять же, ваша первая интерпретация верна. Арифметика без знака следует правилам арифметики по модулю, что означает, что 0x0000 - 0x0001 оценивает 0xFFFF для 32-битных типов без знака.
Однако вторая интерпретация (основанная на "подписанной семантике") также необходима для получения того же результата. Т.е. даже если ты оцениваешь 0 - 1 в домен подписанного типа и получить -1 в качестве промежуточного результата это -1 все еще требуется для производства 0xFFFF когда позже он преобразуется в беззнаковый тип. Даже если какая-то платформа использует экзотическое представление для целых чисел со знаком (дополнение 1, величина со знаком), этой платформе все равно требуется применять правила арифметики по модулю при преобразовании целочисленных значений со знаком в беззнаковые.
Например, эта оценка
signed int a = 0, b = 1;
unsigned int c = a - b;
до сих пор гарантированно производить UINT_MAX в c, даже если платформа использует экзотическое представление для целых чисел со знаком.
С номерами без знака типа unsigned int или больше, в отсутствие преобразования типов, a-b определяется как выдача числа без знака, которое при добавлении к b, даст a, Преобразование отрицательного числа в беззнаковое означает получение числа, которое при добавлении к обратному знаку исходному числу приведет к нулю (поэтому преобразование -5 в беззнаковое даст значение, которое при добавлении к 5 приведет к нулю).,
Обратите внимание, что числа без знака меньше, чем unsigned int может получить повышение по типу int перед вычитанием, поведение a-b будет зависеть от размера int,
int d = abs(five - seven); // d = 2
std::abs не "подходит" для целых чисел без знака. Хотя актерский состав нужен.
Что ж, вычитание целых чисел без знака имеет определенное поведение, к тому же это хитрая штука. Когда вы вычитаете два целых числа без знака, результат повышается до более высокого типа int, если тип результата (lvalue) не указан явно. В последнем случае, например, int8_t result = a - b; (где a и b имеют тип int8_t) вы можете получить очень странное поведение. Я имею в виду, что вы можете потерять свойство транзитивности (т. е. если a > b и b > c, верно, что a > c). Потеря транзитивности может разрушить работу древовидной структуры данных . Необходимо соблюдать осторожность, чтобы не предоставлять функцию сравнения для сортировки, поиска, построения дерева, которое использует вычитание целых чисел без знака, чтобы определить, какой ключ выше или ниже.
См. пример ниже.
#include <stdint.h>
#include <stdio.h>
void main()
{
uint8_t a = 255;
uint8_t b = 100;
uint8_t c = 150;
printf("uint8_t a = %+d, b = %+d, c = %+d\n\n", a, b, c);
printf(" b - a = %+d\tpromotion to int type\n"
" (int8_t)(b - a) = %+d\n\n"
" b + a = %+d\tpromotion to int type\n"
"(uint8_t)(b + a) = %+d\tmodular arithmetic\n"
" b + a %% %d = %+d\n\n",
b - a, (int8_t)(b - a),
b + a, (uint8_t)(b + a),
UINT8_MAX + 1,
(b + a) % (UINT8_MAX + 1));
printf("c %s b (b - c = %d), b %s a (b - a = %d), AND c %s a (c - a = %d)\n",
(int8_t)(c - b) < 0 ? "<" : ">", (int8_t)(c - b),
(int8_t)(b - a) < 0 ? "<" : ">", (int8_t)(b - a),
(int8_t)(c - a) < 0 ? "<" : ">", (int8_t)(c - a));
}
$ ./a.out
uint8_t a = +255, b = +100, c = +150
b - a = -155 promotion to int type
(int8_t)(b - a) = +101
b + a = +355 promotion to int type
(uint8_t)(b + a) = +99 modular arithmetic
b + a % 256 = +99
c > b (b - c = 50), b > a (b - a = 101), AND c < a (c - a = -105)