Ошибки, выполняющие оценку максимального правдоподобия по трехпараметрическому Weibull cdf

Question

Я работаю с кумулятивным появлением мух с течением времени (взятых с нерегулярными интервалами) в течение многих лет (хотя сначала я просто пытаюсь сделать один год работы). Кумулятивное возникновение следует сигмоидальному шаблону, и я хочу создать оценку максимального правдоподобия 3-параметрической кумулятивной функции распределения Вейбулла. Трехпараметрические модели, которые я пытался использовать в fitdistrplus Пакет продолжает давать мне ошибку. Я думаю, что это как-то связано с тем, как мои данные структурированы, но я не могу понять это. Очевидно, я хочу, чтобы он читал каждую точку как x (градусные дни) и y (Появление) значение, но, кажется, не может прочитать два столбца. Основная ошибка, которую я получаю, гласит: "Нечисловой аргумент математической функции" или (с немного другим кодом) "данные должны быть числовым вектором, длина которого больше 1". Ниже мой код, включая добавленные столбцы в df_dd_em рамки данных для совокупного появления и процента появления в случае, если это полезно.

    degree_days <-   c(998.08,1039.66,1111.29,1165.89,1236.53,1293.71,
                      1347.66,1387.76,1445.47,1493.44,1553.23,1601.97,
                      1670.28,1737.29,1791.94,1849.20,1920.91,1967.25,
                      2036.64,2091.85,2152.89,2199.13,2199.13,2263.09,
                      2297.94,2352.39,2384.03,2442.44,2541.28,2663.90,
                      2707.36,2773.82,2816.39,2863.94)
    emergence <-  c(0,0,0,1,1,0,2,3,17,10,0,0,0,2,0,3,0,0,1,5,0,0,0,0,
                   0,0,0,0,1,0,0,0,0,0)
    cum_em <- cumsum(emergence)
    df_dd_em <- data.frame (degree_days, emergence, cum_em)
    df_dd_em$percent <- ave(df_dd_em$emergence, FUN = function(df_dd_em) 100*(df_dd_em)/46)
    df_dd_em$cum_per <- ave(df_dd_em$cum_em, FUN = function(df_dd_em) 100*(df_dd_em)/46)
    x <- pweibull(df_dd_em[c(1,3)],shape=5)
    dframe2.mle <- fitdist(x, "weibull",method='mle')

Answer 1

Вот мое лучшее предположение о том, что вы ищете:

Настроить данные:

dd <- data.frame(degree_days=c(998.08,1039.66,1111.29,1165.89,1236.53,1293.71,
                      1347.66,1387.76,1445.47,1493.44,1553.23,1601.97,
                      1670.28,1737.29,1791.94,1849.20,1920.91,1967.25,
                      2036.64,2091.85,2152.89,2199.13,2199.13,2263.09,
                      2297.94,2352.39,2384.03,2442.44,2541.28,2663.90,
                      2707.36,2773.82,2816.39,2863.94),
                 emergence=c(0,0,0,1,1,0,2,3,17,10,0,0,0,2,0,3,0,0,1,5,0,0,0,0,
                 0,0,0,0,1,0,0,0,0,0))
dd <- transform(dd,cum_em=cumsum(emergence))

На самом деле мы собираемся соответствовать распределению с "цензурой по интервалу" (т. Е. Вероятности появления между последовательными наблюдениями дня степени: эта версия предполагает, что первое наблюдение относится к наблюдениям до наблюдения дня первой степени, вы можете изменить его так, чтобы оно соответствовало наблюдениям после последнего наблюдения).

library(bbmle)
## y*log(p) allowing for 0/0 occurrences:
y_log_p <- function(y,p) ifelse(y==0 & p==0,0,y*log(p))
NLLfun <- function(scale,shape,x=dd$degree_days,y=dd$emergence) {
    prob <- pmax(diff(pweibull(c(-Inf,x),      ## or (c(x,Inf))
             shape=shape,scale=scale)),1e-6)
    ## multinomial probability
    -sum(y_log_p(y,prob))
}    
library(bbmle)

Возможно, мне следовало бы использовать что-то более систематическое, например, метод моментов (то есть сопоставление среднего и дисперсии распределения Вейбулла со средним и дисперсией данных), но я просто немного взломал, чтобы найти правдоподобные начальные значения:

## preliminary look (method of moments would be better)
scvec <- 10^(seq(0,4,length=101))
plot(scvec,sapply(scvec,NLLfun,shape=1))

Важно использовать parscale дать R знать, что параметры находятся в очень разных масштабах:

startvals <- list(scale=1000,shape=1)
m1 <- mle2(NLLfun,start=startvals,
     control=list(parscale=unlist(startvals)))

Теперь попробуйте использовать Weibull с тремя параметрами (как первоначально требовалось) - требуется лишь небольшая модификация того, что у нас уже есть:

library(FAdist)
NLLfun2 <- function(scale,shape,thres,
                    x=dd$degree_days,y=dd$emergence) {
    prob <- pmax(diff(pweibull3(c(-Inf,x),shape=shape,scale=scale,thres)),
                 1e-6)
    ## multinomial probability
    -sum(y_log_p(y,prob))
}    
startvals2 <- list(scale=1000,shape=1,thres=100)
m2 <- mle2(NLLfun2,start=startvals2,
     control=list(parscale=unlist(startvals2)))

Похоже, трехпараметрическая подгонка намного лучше:

library(emdbook)
AICtab(m1,m2)
##    dAIC df
## m2  0.0 3 
## m1 21.7 2 

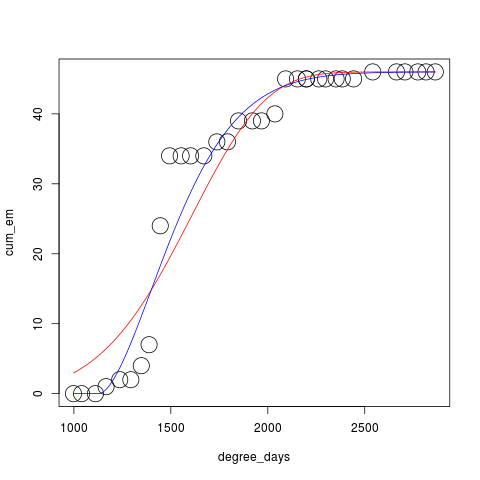
А вот графическое резюме:

with(dd,plot(cum_em~degree_days,cex=3))
with(as.list(coef(m1)),curve(sum(dd$emergence)*
                             pweibull(x,shape=shape,scale=scale),col=2,
                             add=TRUE))
with(as.list(coef(m2)),curve(sum(dd$emergence)*
                             pweibull3(x,shape=shape,
                                       scale=scale,thres=thres),col=4,
                             add=TRUE))

(может также сделать это более элегантно с ggplot2...)

• Они не кажутся удивительно хорошими, но они нормальные. (В принципе, вы можете выполнить критерий соответствия по критерию хи-квадрат, основываясь на ожидаемом количестве аварийных ситуаций за интервал и учитывая тот факт, что вы выбрали трехпараметрическую модель, хотя значения могут быть немного низкими...)
• Доверительные интервалы по подгонке немного неприятны; ваш выбор (1) начальная загрузка; (2) параметрическая начальная загрузка (параметры повторной выборки, предполагающие многомерное нормальное распределение данных); (3) дельта-метод.
• С помощью bbmle::mle2 позволяет легко делать такие вещи, как получение доверительных интервалов профиля:

 confint(m1)
 ##             2.5 %      97.5 %
 ## scale 1576.685652 1777.437283
 ## shape    4.223867    6.318481

Answer 2

dd <- data.frame(degree_days=c(998.08,1039.66,1111.29,1165.89,1236.53,1293.71,
                           1347.66,1387.76,1445.47,1493.44,1553.23,1601.97,
                           1670.28,1737.29,1791.94,1849.20,1920.91,1967.25,
                           2036.64,2091.85,2152.89,2199.13,2199.13,2263.09,
                           2297.94,2352.39,2384.03,2442.44,2541.28,2663.90,
                           2707.36,2773.82,2816.39,2863.94),
             emergence=c(0,0,0,1,1,0,2,3,17,10,0,0,0,2,0,3,0,0,1,5,0,0,0,0,
                         0,0,0,0,1,0,0,0,0,0))

dd$cum_em <- cumsum(dd$emergence)

dd$percent <- ave(dd$emergence, FUN = function(dd) 100*(dd)/46)

dd$cum_per <- ave(dd$cum_em, FUN = function(dd) 100*(dd)/46)

dd <- transform(dd)


#start 3 parameter model

library(FAdist)

## y*log(p) allowing for 0/0 occurrences:

y_log_p <- function(y,p) ifelse(y==0 & p==0,0,y*log(p))

NLLfun2 <- function(scale,shape,thres,
                x=dd$degree_days,y=dd$percent) {
  prob <- pmax(diff(pweibull3(c(-Inf,x),shape=shape,scale=scale,thres)),
           1e-6)
   ## multinomial probability
  -sum(y_log_p(y,prob))
} 

startvals2 <- list(scale=1000,shape=1,thres=100)

m2 <- mle2(NLLfun2,start=startvals2,
       control=list(parscale=unlist(startvals2)))

summary(m2)

#graphical summary

windows(5,5)

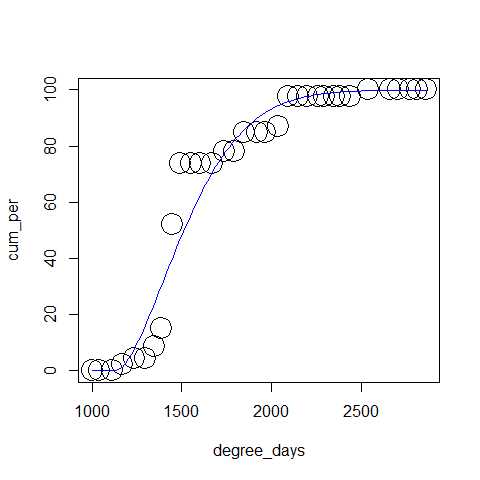
with(dd,plot(cum_per~degree_days,cex=3))

with(as.list(coef(m2)),curve(sum(dd$percent)*
                           pweibull3(x,shape=shape,
                                     scale=scale,thres=thres),col=4,
                         add=TRUE))