XIRR Расчет
Как рассчитать Excel XIRR функция с использованием C#?
5 ответов
В соответствии с документацией openoffice функции XIRR (формула такая же, как в Excel), вам нужно найти переменную XIRR в следующем уравнении f(xirr):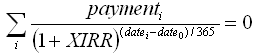
Вы можете рассчитать значение xirr следующим образом:
- вычисление производной вышеуказанной функции -> f '(xirr)
- после
f(xirr)а такжеf'(xirr)Вы можете найти значение xirr, используя итерационный метод Ньютона - знаменитая формула->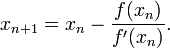
РЕДАКТИРОВАТЬ
У меня есть немного времени, так что вот - полный код C# для расчета XIRR:
class xirr
{
public const double tol = 0.001;
public delegate double fx(double x);
public static fx composeFunctions(fx f1, fx f2) {
return (double x) => f1(x) + f2(x);
}
public static fx f_xirr(double p, double dt, double dt0) {
return (double x) => p*Math.Pow((1.0+x),((dt0-dt)/365.0));
}
public static fx df_xirr(double p, double dt, double dt0) {
return (double x) => (1.0/365.0)*(dt0-dt)*p*Math.Pow((x+1.0),(((dt0-dt)/365.0)-1.0));
}
public static fx total_f_xirr(double[] payments, double[] days) {
fx resf = (double x) => 0.0;
for (int i = 0; i < payments.Length; i++) {
resf = composeFunctions(resf,f_xirr(payments[i],days[i],days[0]));
}
return resf;
}
public static fx total_df_xirr(double[] payments, double[] days) {
fx resf = (double x) => 0.0;
for (int i = 0; i < payments.Length; i++) {
resf = composeFunctions(resf,df_xirr(payments[i],days[i],days[0]));
}
return resf;
}
public static double Newtons_method(double guess, fx f, fx df) {
double x0 = guess;
double x1 = 0.0;
double err = 1e+100;
while (err > tol) {
x1 = x0 - f(x0)/df(x0);
err = Math.Abs(x1-x0);
x0 = x1;
}
return x0;
}
public static void Main (string[] args)
{
double[] payments = {-6800,1000,2000,4000}; // payments
double[] days = {01,08,16,25}; // days of payment (as day of year)
double xirr = Newtons_method(0.1,
total_f_xirr(payments,days),
total_df_xirr(payments,days));
Console.WriteLine("XIRR value is {0}", xirr);
}
}
Кстати, имейте в виду, что не все платежи приведут к действительному XIRR из-за ограничений формулы и / или метода Ньютона!
ура!
Я начал с решения Agnius Vasiliauskas, но в итоге некоторые новые сценарии привели к сбою метода Ньютона. Я создал "умную" версию, которая использует метод деления пополам (медленнее) при сбое Ньютона.
Обратите внимание на встроенные ссылки на несколько источников, которые я использовал для этого решения.
Наконец, вы не сможете воспроизвести некоторые из этих сценариев в Excel, поскольку Excel сам использует метод Ньютона. Обратитесь к XIRR, а? за интересную дискуссию по этому поводу.
используя Систему; using System.Collections.Generic; использование System.Linq;// Смотрите следующие статьи: // http://blogs.msdn.com/b/lucabol/archive/2007/12/17/bisection-based-xirr-implementation-in-c.aspx // http://www.codeproject.com/Articles/79541/Three-Methods-for-Root-finding-in-C // http://www.financialwebring.org/forum/viewtopic.php?t=105243&highlight=xirr // Значения по умолчанию на основе Excel doc // http://office.microsoft.com/en-us/excel-help/xirr-function-HP010062387.aspx
пространство имен Xirr { Программа общественного класса { private const Double DaysPerYear = 365,0; private const int MaxIterations = 100; private const double DefaultTolerance = 1E-6; private const double DefaultGuess = 0,1;
private static readonly Func<IEnumerable<CashItem>, Double> NewthonsMethod = cf => NewtonsMethodImplementation(cf, Xnpv, XnpvPrime); private static readonly Func<IEnumerable<CashItem>, Double> BisectionMethod = cf => BisectionMethodImplementation(cf, Xnpv); public static void Main(string[] args) { RunScenario(new[] { // this scenario fails with Newton's but succeeds with slower Bisection new CashItem(new DateTime(2012, 6, 1), 0.01), new CashItem(new DateTime(2012, 7, 23), 3042626.18), new CashItem(new DateTime(2012, 11, 7), -491356.62), new CashItem(new DateTime(2012, 11, 30), 631579.92), new CashItem(new DateTime(2012, 12, 1), 19769.5), new CashItem(new DateTime(2013, 1, 16), 1551771.47), new CashItem(new DateTime(2013, 2, 8), -304595), new CashItem(new DateTime(2013, 3, 26), 3880609.64), new CashItem(new DateTime(2013, 3, 31), -4331949.61) }); RunScenario(new[] { new CashItem(new DateTime(2001, 5, 1), 10000), new CashItem(new DateTime(2002, 3, 1), 2000), new CashItem(new DateTime(2002, 5, 1), -5500), new CashItem(new DateTime(2002, 9, 1), 3000), new CashItem(new DateTime(2003, 2, 1), 3500), new CashItem(new DateTime(2003, 5, 1), -15000) }); } private static void RunScenario(IEnumerable<CashItem> cashFlow) { try { try { var result = CalcXirr(cashFlow, NewthonsMethod); Console.WriteLine("XIRR [Newton's] value is {0}", result); } catch (InvalidOperationException) { // Failed: try another algorithm var result = CalcXirr(cashFlow, BisectionMethod); Console.WriteLine("XIRR [Bisection] (Newton's failed) value is {0}", result); } } catch (ArgumentException e) { Console.WriteLine(e.Message); } catch (InvalidOperationException exception) { Console.WriteLine(exception.Message); } } private static double CalcXirr(IEnumerable<CashItem> cashFlow, Func<IEnumerable<CashItem>, double> method) { if (cashFlow.Count(cf => cf.Amount > 0) == 0) throw new ArgumentException("Add at least one positive item"); if (cashFlow.Count(c => c.Amount < 0) == 0) throw new ArgumentException("Add at least one negative item"); var result = method(cashFlow); if (Double.IsInfinity(result)) throw new InvalidOperationException("Could not calculate: Infinity"); if (Double.IsNaN(result)) throw new InvalidOperationException("Could not calculate: Not a number"); return result; } private static Double NewtonsMethodImplementation(IEnumerable<CashItem> cashFlow, Func<IEnumerable<CashItem>, Double, Double> f, Func<IEnumerable<CashItem>, Double, Double> df, Double guess = DefaultGuess, Double tolerance = DefaultTolerance, int maxIterations = MaxIterations) { var x0 = guess; var i = 0; Double error; do { var dfx0 = df(cashFlow, x0); if (Math.Abs(dfx0 - 0) < Double.Epsilon) throw new InvalidOperationException("Could not calculate: No solution found. df(x) = 0"); var fx0 = f(cashFlow, x0); var x1 = x0 - fx0/dfx0; error = Math.Abs(x1 - x0); x0 = x1; } while (error > tolerance && ++i < maxIterations); if (i == maxIterations) throw new InvalidOperationException("Could not calculate: No solution found. Max iterations reached."); return x0; } internal static Double BisectionMethodImplementation(IEnumerable<CashItem> cashFlow, Func<IEnumerable<CashItem>, Double, Double> f, Double tolerance = DefaultTolerance, int maxIterations = MaxIterations) { // From "Applied Numerical Analysis" by Gerald var brackets = Brackets.Find(Xnpv, cashFlow); if (Math.Abs(brackets.First - brackets.Second) < Double.Epsilon) throw new ArgumentException("Could not calculate: bracket failed"); Double f3; Double result; var x1 = brackets.First; var x2 = brackets.Second; var i = 0; do { var f1 = f(cashFlow, x1); var f2 = f(cashFlow, x2); if (Math.Abs(f1) < Double.Epsilon && Math.Abs(f2) < Double.Epsilon) throw new InvalidOperationException("Could not calculate: No solution found"); if (f1*f2 > 0) throw new ArgumentException("Could not calculate: bracket failed for x1, x2"); result = (x1 + x2)/2; f3 = f(cashFlow, result); if (f3*f1 < 0) x2 = result; else x1 = result; } while (Math.Abs(x1 - x2)/2 > tolerance && Math.Abs(f3) > Double.Epsilon && ++i < maxIterations); if (i == maxIterations) throw new InvalidOperationException("Could not calculate: No solution found"); return result; } private static Double Xnpv(IEnumerable<CashItem> cashFlow, Double rate) { if (rate <= -1) rate = -1 + 1E-10; // Very funky ... Better check what an IRR <= -100% means var startDate = cashFlow.OrderBy(i => i.Date).First().Date; return (from item in cashFlow let days = -(item.Date - startDate).Days select item.Amount*Math.Pow(1 + rate, days/DaysPerYear)).Sum(); } private static Double XnpvPrime(IEnumerable<CashItem> cashFlow, Double rate) { var startDate = cashFlow.OrderBy(i => i.Date).First().Date; return (from item in cashFlow let daysRatio = -(item.Date - startDate).Days/DaysPerYear select item.Amount*daysRatio*Math.Pow(1.0 + rate, daysRatio - 1)).Sum(); } public struct Brackets { public readonly Double First; public readonly Double Second; public Brackets(Double first, Double second) { First = first; Second = second; } internal static Brackets Find(Func<IEnumerable<CashItem>, Double, Double> f, IEnumerable<CashItem> cashFlow, Double guess = DefaultGuess, int maxIterations = MaxIterations) { const Double bracketStep = 0.5; var leftBracket = guess - bracketStep; var rightBracket = guess + bracketStep; var i = 0; while (f(cashFlow, leftBracket)*f(cashFlow, rightBracket) > 0 && i++ < maxIterations) { leftBracket -= bracketStep; rightBracket += bracketStep; } return i >= maxIterations ? new Brackets(0, 0) : new Brackets(leftBracket, rightBracket); } } public struct CashItem { public DateTime Date; public Double Amount; public CashItem(DateTime date, Double amount) { Date = date; Amount = amount; } } }
}
Спасибо авторам пакета nuget, расположенного в Excel Financial Functions. Он поддерживает множество финансовых методов - AccrInt, Irr, Npv, Pv, XIrr, XNpv и т. Д.,
- Установите и импортируйте пакет.
- Поскольку все методы в классе Financial являются статическими, вызовите конкретный метод как
Financial.<method_name>с необходимыми параметрами.
Пример:
using Excel.FinancialFunctions;
namespace ExcelXirr
{
class Program
{
static void Main(string[] args)
{
List<double> valList =new List<double>();
valList.Add(4166.67);
valList.Add(-4166.67);
valList.Add(-4166.67);
valList.Add(-4166.67);
List<DateTime> dtList = new List<DateTime>();
dtList.Add(new DateTime(2014, 9, 1));
dtList.Add(new DateTime(2014, 10, 1));
dtList.Add(new DateTime(2014, 11, 1));
dtList.Add(new DateTime(2014, 12, 1));
double result = Financial.XIrr(valList, dtList);
Console.WriteLine(result);
Console.ReadLine();
}
}
}
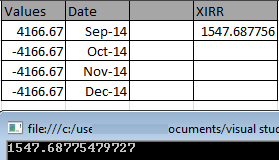
Результат такой же, как в Excel.
Другие ответы показывают, как реализовать XIRR в C#, но если требуется только результат вычисления, вы можете напрямую вызвать функцию XIRR в Excel следующим образом:
Сначала добавьте ссылку на Microsoft.Office.Interop.Excel, а затем используйте следующий метод:
public static double Xirr(IList<double> values, IList<DateTime> dates)
{
var xlApp = new Application();
var datesAsDoubles = new List<double>();
foreach (var date in dates)
{
var totalDays = (date - DateTime.MinValue).TotalDays;
datesAsDoubles.Add(totalDays);
}
var valuesArray = values.ToArray();
var datesArray = datesAsDoubles.ToArray();
return xlApp.WorksheetFunction.Xirr(valuesArray, datesArray);
}
В этом репо с GitHub - klearlending / XIRR есть пример кода о том, как рассчитать XIRR.
Автор также предоставил пост в блоге, демистифицированный XIRR , который объясняет логику и рассуждения.
Пока что эта библиотека дает мне близкие к точным результаты. (Все еще исследую его и разветвил для личного использования)