Кубическая кривая Безье, не возвращающая правильное значение Y, заданное (t, p0, p1, p2, p3)

Question

Моя цель - написать анимацию на JavaScript, которая выполняет анимацию кривой Безье в стиле easy-in-out (например, в http://cubic-bezier.com/)

Я придумал следующий скрипт для вычисления значения y с учетом значения "x" (время):

function CalculateBezierPoint(t, p0, p1, p2, p3) {
  var y = ((1-t)*(1-t)*(1-t)*p0) + (3*(1-t)*(1-t)*t*p1) + (3*(1-t)*t*t*p2) + (t*t*t*p3);
  return y;
}

Используя явную формулу из Википедии: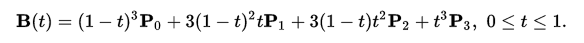

Демо - https://codepen.io/anon/pen/QpRzBg

Тем не менее, операторы печати показывают, что значение Y уменьшается до того, как повышается, когда оно должно увеличиваться ТОЛЬКО:

0.42
0.3228427793606603
0.3119941308275725
0.3025864871426283
0.29458762995005683
0.2879653408940873
0.28268740161894895
0.27872159376887096
0.27603569898808256
0.27459749892081287
0.2743747752112911
0.2753353095037466
0.27744688344240837
0.28067727867150566
0.2849942768352678
0.29675920854370297
0.3041427053768346
0.3124839317215477
0.3217506690862967
0.33191069937460593
0.34293180410763435
0.35478176492961133

Мне удалось найти чей-то код, который, кажется, работает, вот вывод:

0
0.009480343767040133
0.0246451904411195
0.03199616010201068
0.040680303103589804
0.05080871722437687
0.062492500242891866
0.07584274993765482
0.0909705640871857
0.10798704047000454
0.12700327686463134
0.14813037104958607
0.17147942080338874
0.19716152390455938
0.225287778131618
0.25596928126308455
0.28931713107747903
0.3254424253533215
0.36445626186913194
0.4064697384034303
0.4515939527347367
0.499940002641571

Демо - https://codepen.io/anon/pen/evabrr

Обе демонстрации используют один и тот же вход: p0 = .42, p1 = 0, p2 = .58, p3 = 1

Я не знаю, почему моя попытка не удалась, и код, который я нашел, работает. Я неправильно реализовал формулу? Я выбрал неправильную формулу? Что-то другое?

Answer 1

Таким образом, ваша ошибка - не передать ни единого значения, ни степенной функции. Ошибка в том, что вы предполагаете, что x = t.

Я придумал следующий скрипт для вычисления значения y с учетом значения "x" (время):

Если x = t, то у вас есть явная кривая Безье, а не параметрическая кривая Безье. Явное значение, что у является функцией х (т. Е. У = F (х)). В отличие от параметрического уравнения, где и x, и y являются функциями t (то есть x=f(t) и y=f(t)).

Один из способов проверить, что это действительно так, установить значения x в [0, 1/3, 2/3, 1]. Равномерно распределенные значения x гарантируют, что x = t, и дадут вам явную кривую Безье. Вы можете добиться этого на http://cubic-bezier.com/, установив значения x в адресной строке на 0,333 и 0,666. Но как только вы переместите контрольные точки влево или вправо, ваши результаты снова будут отличаться.

Чтобы получить тот же эффект, это немного сложнее. Вы должны решить для t в данном x и затем вычислить y из t. Решение для t немного сложное, но может быть аппроксимировано методом Ньютона-Рафсона. Эта ссылка гораздо лучше объясняет, как ее реализовать: http://greweb.me/2012/02/bezier-curve-based-easing-functions-from-concept-to-implementation/

Answer 2

Поздно к вечеринке, но: ваш комментарий "Я думаю, что на самом деле я делаю большую ошибку - предполагается, что P - это точечные значения, которые должны иметь (x,y), и я предоставляю только одну цифру" правильный.

Кривая Безье - это параметрическая функция, где и x, и y (или x, y и z в 3D) являются функциями t. Вы рассчитываете только половину кривой, поэтому вам нужно изменить CalculateBezierPoint функция для возврата координаты x/y, а не только координаты y:

calculateBezierPoint(t, xvalues, yvalues) {
  return new Point(
    x = calculateBezierDim(t, x1, x2, x3, x4),
    y = calculateBezierDim(t, y1, y2, y3,y4)
  );
}

calculateBezierDim(t, vals) {
  a=vals[0], b=vals[1], c=vals[2], d=vals[3];
  mt = 1-t;
  t2 = t*t;
  mt2 = mt*mt;
  return a * mt*mt2 + 3 * b * mt2 * t + 3 * c * mt * t2 + d * t2 * t;
}

(Адаптировано к вашему языку программирования и типам данных, конечно).

Тогда вы можете нарисовать эту координату х / у.

step = some small value
S = calculateBezierPoint(0, xvals, yvals)
for(t=step; t<1+step; t+=step) {
  E = calculateBezierPoint(t, xvals, yvals)
  drawLine(S.x, S.y, E.x, E.y)
  S = E
}

Answer 3

Я думаю, что в вашей формуле может быть ошибка с приоритетом оператора. Я бы попытался использовать функцию возведения в степень, где это уместно, чтобы было легче отлаживать.

Math.pow(base, exponent)