Правильная реализация кубической сплайн-интерполяции
Я использовал один из предложенных алгоритмов, но результаты очень плохие.
Я реализовал алгоритм вики
в Java (код ниже). x(0) является points.get(0), y(0) является values[points.get(0)], α является alfa а также μ является mi, Остальное такое же, как в псевдокоде вики.
public void createSpline(double[] values, ArrayList<Integer> points){
a = new double[points.size()+1];
for (int i=0; i <points.size();i++)
{
a[i] = values[points.get(i)];
}
b = new double[points.size()];
d = new double[points.size()];
h = new double[points.size()];
for (int i=0; i<points.size()-1; i++){
h[i] = points.get(i+1) - points.get(i);
}
alfa = new double[points.size()];
for (int i=1; i <points.size()-1; i++){
alfa[i] = (double)3 / h[i] * (a[i+1] - a[i]) - (double)3 / h[i-1] *(a[i+1] - a[i]);
}
c = new double[points.size()+1];
l = new double[points.size()+1];
mi = new double[points.size()+1];
z = new double[points.size()+1];
l[0] = 1; mi[0] = z[0] = 0;
for (int i =1; i<points.size()-1;i++){
l[i] = 2 * (points.get(i+1) - points.get(i-1)) - h[i-1]*mi[i-1];
mi[i] = h[i]/l[i];
z[i] = (alfa[i] - h[i-1]*z[i-1])/l[i];
}
l[points.size()] = 1;
z[points.size()] = c[points.size()] = 0;
for (int j=points.size()-1; j >0; j--)
{
c[j] = z[j] - mi[j]*c[j-1];
b[j] = (a[j+1]-a[j]) - (h[j] * (c[j+1] + 2*c[j])/(double)3) ;
d[j] = (c[j+1]-c[j])/((double)3*h[j]);
}
for (int i=0; i<points.size()-1;i++){
for (int j = points.get(i); j<points.get(i+1);j++){
// fk[j] = values[points.get(i)];
functionResult[j] = a[i] + b[i] * (j - points.get(i))
+ c[i] * Math.pow((j - points.get(i)),2)
+ d[i] * Math.pow((j - points.get(i)),3);
}
}
}
В результате я получаю следующее:
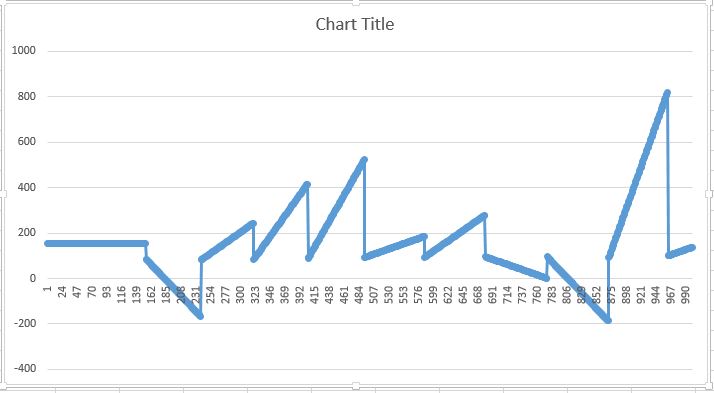
но это должно быть похоже на это:
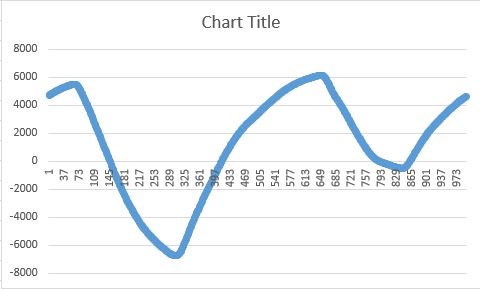
Я также пытаюсь реализовать алгоритм по-другому в соответствии с: http://www.geos.ed.ac.uk/~yliu23/docs/lect_spline.pdf
Сначала они показывают, как сделать линейный сплайн, и это довольно просто. Я создаю функции, которые рассчитывают A а также B коэффициенты. Затем они расширяют линейный сплайн, добавляя вторую производную. C а также D Коэффициенты тоже легко рассчитать.
Но проблемы начинаются, когда я пытаюсь вычислить вторую производную. Я не понимаю, как они их рассчитывают.
Поэтому я реализовал только линейную интерполяцию. Результат:
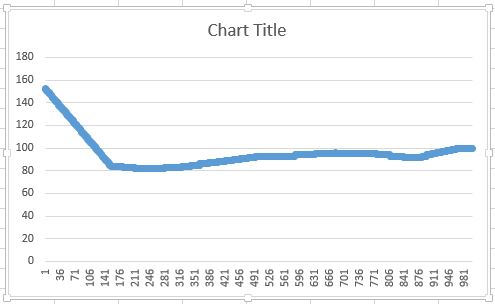
Кто-нибудь знает, как исправить первый алгоритм или объяснить, как рассчитать вторую производную во втором алгоритме?
3 ответа
Извините, но Ваш исходный код действительно нечитаемый беспорядок для меня, поэтому я придерживаюсь теории. Вот несколько советов:
SPLINE кубики
SPLINE - это не интерполяция, а приближение для их использования, вам не нужно никакого вывода. Если у вас есть десять очков:
p0,p1,p2,p3,p4,p5,p6,p7,p8,p9затем кубический сплайн начинается / заканчивается тройной точкой. Если вы создадите функцию для "рисования" патча кубической кривой SPLINE, то для обеспечения непрерывности последовательность вызовов будет выглядеть следующим образом:spline(p0,p0,p0,p1); spline(p0,p0,p1,p2); spline(p0,p1,p2,p3); spline(p1,p2,p3,p4); spline(p2,p3,p4,p5); spline(p3,p4,p5,p6); spline(p4,p5,p6,p7); spline(p5,p6,p7,p8); spline(p6,p7,p8,p9); spline(p7,p8,p9,p9); spline(p8,p9,p9,p9);не забывайте, что кривая SPLINE для
p0,p1,p2,p3нарисовать только кривую "между"p1,p2!!!Безье кубики
Четырехточечные коэффициенты БЕЗЬЕРА могут быть вычислены следующим образом:
a0= ( p0); a1= (3.0*p1)-(3.0*p0); a2= (3.0*p2)-(6.0*p1)+(3.0*p0); a3=( p3)-(3.0*p2)+(3.0*p1)-( p0);интерполирование
чтобы использовать интерполяцию, вы должны использовать интерполяционные полиномы. Есть много, но я предпочитаю использовать кубики... похожие на BEZIER/SPLINE/NURBS... так
p(t) = a0+a1*t+a2*t*t+a3*t*t*tгдеt = <0,1>
Осталось только вычислить
a0,a1,a2,a3, У вас есть 2 уравнения (p(t)и его вывод поt) и 4 балла из набора данных. Вы также должны обеспечить непрерывность... Таким образом, первый вывод для точек соединения должен быть одинаковым для соседних кривых (t=0,t=1). Это приводит к системе 4 линейных уравнений (использованиеt=0а такжеt=1). Если вы получите его, то создадите простое уравнение, зависящее только от координат входной точки:double d1,d2; d1=0.5*(p2-p0); d2=0.5*(p3-p1); a0=p1; a1=d1; a2=(3.0*(p2-p1))-(2.0*d1)-d2; a3=d1+d2+(2.0*(-p2+p1));последовательность вызовов такая же, как для SPLINE
[Заметки]
Разница между интерполяцией и аппроксимацией заключается в том, что:
Кривая интерполяции всегда проходит через контрольные точки, но многочлены высокого порядка имеют тенденцию колебаться, и приближение только приближается к контрольным точкам (в некоторых случаях может пересекать их, но обычно нет).
переменные:
a0,... p0,...являются векторами (число измерений должно соответствовать входным точкам)tявляется скалярным
рисовать кубики из коэффициентов
a0,..a3просто сделайте что-то вроде этого:
MoveTo(a0.x,a0.y); for (t=0.0;t<=1.0;t+=0.01) { tt=t*t; ttt=tt*t; p=a0+(a1*t)+(a2*tt)+(a3*ttt); LineTo(p.x,p.y); }
Кубический b-сплайн был недавно описан в серии работ Unser, Thévenaz et al. смотрите среди других
М. Унсер, А. Алдруби, М. Иден, "Быстрые B-сплайн-преобразования для непрерывного представления и интерполяции изображений", IEEE Trans. Pattern Анальный. Машина Интелл. том 13, н. 3, с. 277-285, март 1991 г.
М. Unser, "Сплайны, идеально подходящие для обработки сигналов и изображений", IEEE Signal Proc. Магнето, с. 22- 38, ноябрь 1999 г.
а также
P. Thévenaz, T. Blu, M. Unser, "Возвращение к интерполяции", IEEE Trans. по медицинской визуализации, том. 19, нет. 7, с. 739-758, июль 2000 г.
Вот несколько рекомендаций.
Что такое сплайны?
Сплайны - это кусочно-полиномы, которые гладко связаны друг с другом. За сплайн степени n каждый сегмент является полиномом степени n, Части связаны так, что сплайн непрерывен до его производной степени n-1 в узлах, а именно, в точках соединения полиномов.
Как можно построить сплайны?
Сплайн нулевого порядка следующий
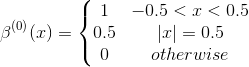
Все остальные сплайны могут быть построены как
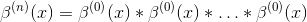
где сверток взят n-1 раз.
Кубические сплайны
Самые популярные сплайны - кубические сплайны, чье выражение
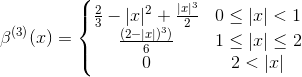
Сплайн-интерполяция
Учитывая функцию f(x) выборка в дискретных целочисленных точках k, задача сплайн-интерполяции состоит в определении аппроксимации s(x) в f(x) выражается следующим образом
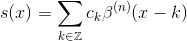
где ck это коэффициенты интерполяции и s(k) = f(k),
Сплайн-предварительная фильтрация
К сожалению, начиная с n=3 на,
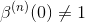
таким образом ck это не коэффициенты интерполяции. Их можно определить, решив линейную систему уравнений, полученную путем принуждения s(k) = f(k) а именно

Такое уравнение может быть преобразовано в форму свертки и решено в преобразованном z пространство как
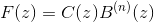
где
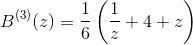
Соответственно,

Такой путь всегда предпочтительнее, чем решение линейной системы уравнений, например, LU разложение.
Решение вышеприведенного уравнения можно определить, заметив, что
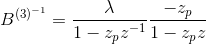
где
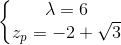
Первая фракция является показателем причинного фильтра, а вторая - антикаузальным фильтром. Оба они показаны на рисунках ниже.
Причинный фильтр
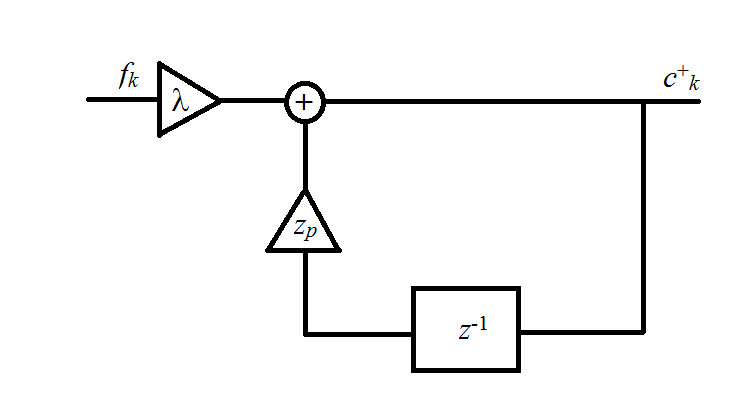
Антикаузальный фильтр
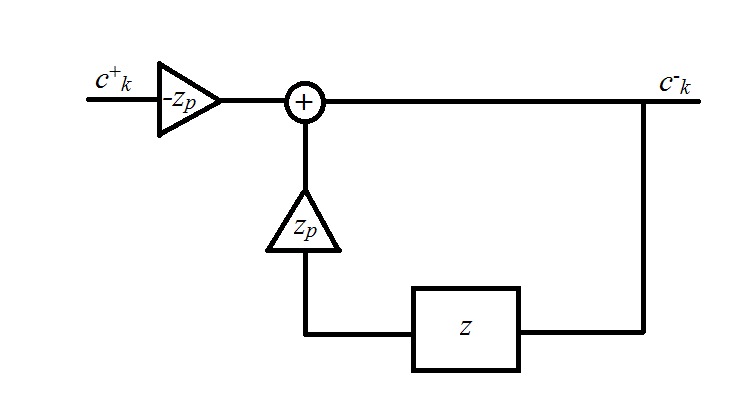
На последнем рисунке
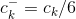
Выходные данные фильтров могут быть выражены следующими рекурсивными уравнениями
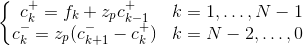
Вышеприведенные уравнения могут быть решены путем первого определения "начальных условий" для c- а также c+, При допущении периодической зеркальной входной последовательности fk такой, что
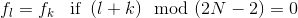
тогда можно показать, что начальное условие для c+ может быть выражено как
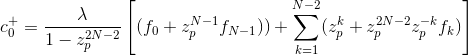
в то время как начальное условие для c+ может быть выражено как

См. Сплайн-интерполяцию, хотя они дают только полезный пример 3x3. Для большего количества точек выборки, скажем, N+1 перечислил x[0..N] со значениями y[0..N] нужно решить следующую систему для неизвестного k[0..N]
2* c[0] * k[0] + c[0] * k[1] == 3* d[0];
c[0] * k[0] + 2*(c[0]+c[1]) * k[1] + c[1] * k[2] == 3*(d[0]+d[1]);
c[1] * k[1] + 2*(c[1]+c[2]) * k[2] + c[2] * k[3] == 3*(d[1]+d[2]);
c[2] * k[2] + 2*(c[2]+c[3]) * k[3] + c[3] * k[4] == 3*(d[2]+d[3]);
...
c[N-2]*k[N-2]+2*(c[N-2]+c[N-1])*k[N-1]+c[N-1]*k[N] == 3*(d[N-2]+d[N-1]);
c[N-2]*k[N-1] + 2*c[N-1] * k[N] == 3* d[N-1];
где
c[k]=1/(x[k+1]-x[k]); d[k]=(y[k+1]-y[k])*c[k]*c[k];
Эту проблему можно решить с помощью итерации Гаусса-Зайделя (не было ли она изобретена именно для этой системы?) Или вашего любимого космического решателя Крылова.
// Файл: cbspline-test.cpp
// C++ Cubic Spline Interpolation using the Boost library.
// Interpolation is an estimation of a value within two known values in a sequence of values.
// From a selected test function y(x) = (5.0/(x))*sin(5*x)+(x-6), 21 numbers of (x,y) equal-spaced sequential points were generated.
// Using the known 21 (x,y) points, 1001 numbers of (x,y) equal-spaced cubic spline interpolated points were calculated.
// Since the test function y(x) is known exactly, the exact y-value for any x-value can be calculated.
// For each point, the interpolation error is calculated as the difference between the exact (x,y) value and the interpolated (x,y) value.
// This program writes outputs as tab delimited results to both screen and named text file
// COMPILATION: $ g++ -lgmp -lm -std=c++11 -o cbspline-test.xx cbspline-test.cpp
// EXECUTION: $ ./cbspline-test.xx
// GNUPLOT 1: gnuplot> load "cbspline-versus-exact-function-plots.gpl"
// GNUPLOT 2: gnuplot> load "cbspline-interpolated-point-errors.gpl"
#include <iostream>
#include <fstream>
#include <boost/math/interpolators/cubic_b_spline.hpp>
using namespace std;
// ========================================================
int main(int argc, char* argv[]) {
// ========================================================
// Vector size 21 = 20 space intervals, size 1001 = 1000 space intervals
std::vector<double> x_knot(21), x_exact(1001), x_cbspline(1001);
std::vector<double> y_knot(21), y_exact(1001), y_cbspline(1001);
std::vector<double> y_diff(1001);
double x; double x0 = 0.0; double t0 = 0.0;
double xstep1 = 0.5; double xstep2 = 0.01;
ofstream outfile; // Output data file tab delimited values
outfile.open("cbspline-errors-1000-points.dat"); // y_diff = (y_exact - y_cbspline)
// Handling zero-point infinity (1/x) when x = 0
x0 = 1e-18;
x_knot[0] = x0;
y_knot[0] = (5.0/(x0))*sin(5*x0)+(x0-6); // Selected test function
for (int i = 1; i <= 20; i++) { // Note: Loop i begins with 1 not 0, 20 points
x = (i*xstep1);
x_knot[i] = x;
y_knot[i] = (5.0/(x))*sin(5*x)+(x-6);
}
// Execution of the cubic spline interpolation from Boost library
// NOTE: Using xstep1 = 0.5 based on knot points stepsize (for 21 known points)
boost::math::cubic_b_spline<double> spline(y_knot.begin(), y_knot.end(), t0, xstep1);
// Again handling zero-point infinity (1/x) when x = 0
x_cbspline[0] = x_knot[0];
y_cbspline[0] = y_knot[0];
for (int i = 1; i <= 1000; ++i) { // 1000 points.
x = (i*xstep2);
x_cbspline[i] = x;
// NOTE: y = spline(x) is valid for any value of x in xrange [0:10]
// meaning, any x within range [x_knot.begin() and x_knot.end()]
y_cbspline[i] = spline(x);
}
// Write headers for screen display and output file
std::cout << "# x_exact[i] \t y_exact[i] \t y_cbspline[i] \t (y_diff[i])" << std::endl;
outfile << "# x_exact[i] \t y_exact[i] \t y_cbspline[i] \t (y_diff[i])" << std::endl;
// Again handling zero-point infinity (1/x) when x = 0
x_exact[0] = x_knot[0];
y_exact[0] = y_knot[0];
y_diff[0] = (y_exact[0] - y_cbspline[0]);
std::cout << x_exact[0] << "\t" << y_exact[0] << "\t" << y_cbspline[0] << "\t" << y_diff[0] << std::endl; // Write to screen
outfile << x_exact[0] << "\t" << y_exact[0] << "\t" << y_cbspline[0] << "\t" << y_diff[0] << std::endl; // Write to text file
for (int i = 1; i <= 1000; ++i) { // 1000 points
x = (i*xstep2);
x_exact[i] = x;
y_exact[i] = (5.0/(x))*sin(5*x)+(x-6);
y_diff[i] = (y_exact[i] - y_cbspline[i]);
std::cout << x_exact[i] << "\t" << y_exact[i] << "\t" << y_cbspline[i] << "\t" << y_diff[i] << std::endl; // Write to screen
outfile << x_exact[i] << "\t" << y_exact[i] << "\t" << y_cbspline[i] << "\t" << y_diff[i] << std::endl; // Write to text file
}
outfile.close();
return(0);
}
// ========================================================
/*
# GNUPLOT script 1
# File: cbspline-versus-exact-function-plots.gpl
set term qt persist size 700,500
set xrange [-1:10.0]
set yrange [-12.0:20.0]
# set autoscale # set xtics automatically
set xtics 0.5
set ytics 2.0
# set xtic auto # set xtics automatically
# set ytic auto # set ytics automatically
set grid x
set grid y
set xlabel "x"
set ylabel "y(x)"
set title "Function points y(x) = (5.0/(x))*sin(5*x)+(x-6)"
set yzeroaxis linetype 3 linewidth 1.5 linecolor 'black'
set xzeroaxis linetype 3 linewidth 1.5 linecolor 'black'
show xzeroaxis
show yzeroaxis
show grid
plot 'cbspline-errors-1000-points.dat' using 1:2 with lines linetype 3 linewidth 1.0 linecolor 'blue' title 'exact function curve', 'cbspline-errors-1000-points.dat' using 1:3 with lines linecolor 'red' linetype 3 linewidth 1.0 title 'cubic spline interpolated curve'
*/
// ========================================================
/*
# GNUPLOT script 2
# File: cbspline-interpolated-point-errors.gpl
set term qt persist size 700,500
set xrange [-1:10.0]
set yrange [-2.50:2.5]
# set autoscale # set xtics automatically
set xtics 0.5
set ytics 0.5
# set xtic auto # set xtics automatically
# set ytic auto # set ytics automatically
set grid x
set grid y
set xlabel "x"
set ylabel "y"
set title "Function points y = (5.0/(x))*sin(5*x)+(x-6)"
set yzeroaxis linetype 3 linewidth 1.5 linecolor 'black'
set xzeroaxis linetype 3 linewidth 1.5 linecolor 'black'
show xzeroaxis
show yzeroaxis
show grid
plot 'cbspline-errors-1000-points.dat' using 1:4 with lines linetype 3 linewidth 1.0 linecolor 'red' title 'cubic spline interpolated errors'
*/
// ========================================================