В чем разница между ACF панд и statsmodel ACF?

Я рассчитываю функцию автокорреляции для доходности акций. Для этого я протестировал две функции, autocorr функция, встроенная в панд, и acf функция предоставлена statsmodels.tsa, Это сделано в следующем MWE:

import pandas as pd
from pandas_datareader import data
import matplotlib.pyplot as plt
import datetime
from dateutil.relativedelta import relativedelta
from statsmodels.tsa.stattools import acf, pacf

ticker = 'AAPL'
time_ago = datetime.datetime.today().date() - relativedelta(months = 6)

ticker_data = data.get_data_yahoo(ticker, time_ago)['Adj Close'].pct_change().dropna()
ticker_data_len = len(ticker_data)

ticker_data_acf_1 =  acf(ticker_data)[1:32]
ticker_data_acf_2 = [ticker_data.autocorr(i) for i in range(1,32)]

test_df = pd.DataFrame([ticker_data_acf_1, ticker_data_acf_2]).T
test_df.columns = ['Pandas Autocorr', 'Statsmodels Autocorr']
test_df.index += 1
test_df.plot(kind='bar')

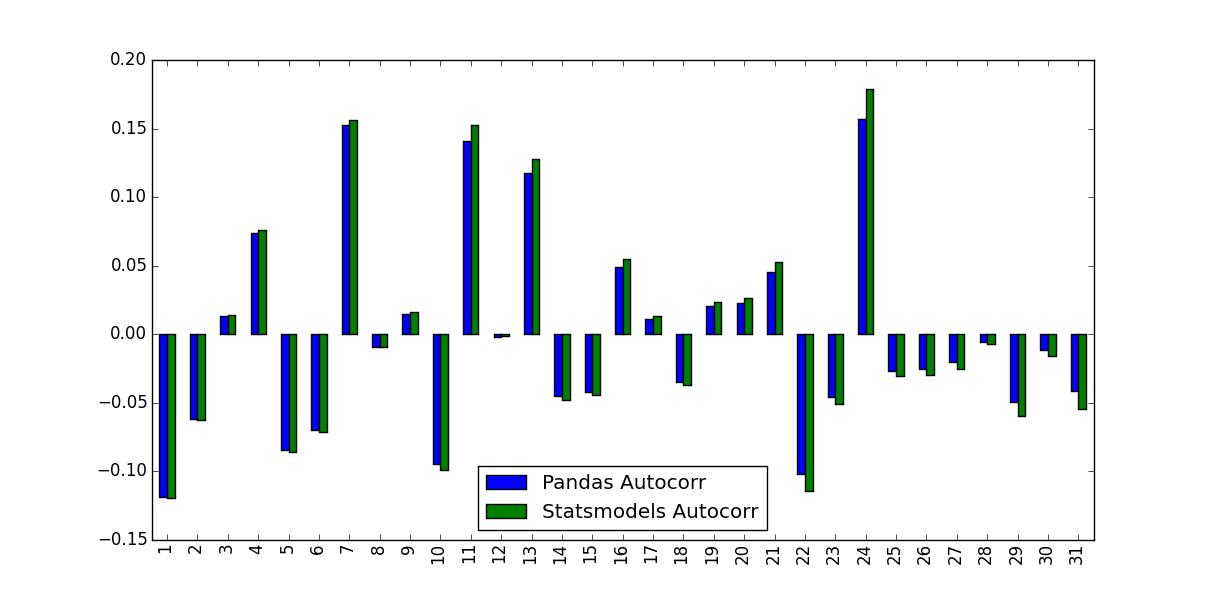
То, что я заметил, было значениями, которые они предсказывали, не были идентичны:

введите описание изображения здесь

Чем объясняется эта разница и какие значения следует использовать?

Источник

2 ответа

Решение

Разница между версией Pandas и Statsmodels заключается в среднем вычитании и делении нормализации / дисперсии:

  • autocorr не делает ничего, кроме передачи подсерии оригинальной серии np.corrcoef, Внутри этого метода выборочное среднее и выборочное отклонение этих подсерий используются для определения коэффициента корреляции.
  • acfнапротив, для определения коэффициента корреляции используется среднее значение выборки для всей серии и дисперсия выборки.

Различия могут уменьшаться для более длинных временных рядов, но довольно велики для коротких.

По сравнению с Matlab, Панды autocorr функция, вероятно, соответствует делать Matlabs xcorr (cross-corr) с самими (отстающими) рядами вместо матлаба autocorr, который вычисляет образец автокорреляции (догадываясь из документов; я не могу проверить это, потому что у меня нет доступа к Matlab).

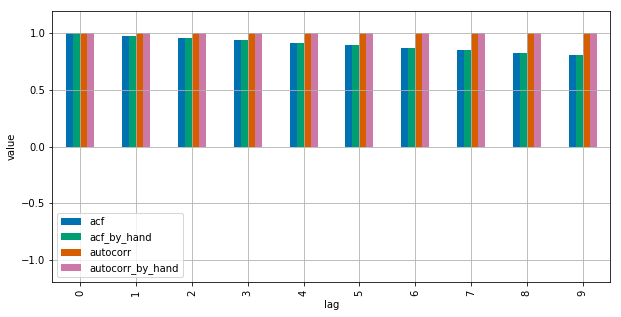
Смотрите это MWE для уточнения:

import numpy as np
import pandas as pd
from statsmodels.tsa.stattools import acf
import matplotlib.pyplot as plt
plt.style.use("seaborn-colorblind")

def autocorr_by_hand(x, lag):
    # Slice the relevant subseries based on the lag
    y1 = x[:(len(x)-lag)]
    y2 = x[lag:]
    # Subtract the subseries means
    sum_product = np.sum((y1-np.mean(y1))*(y2-np.mean(y2)))
    # Normalize with the subseries stds
    return sum_product / ((len(x) - lag) * np.std(y1) * np.std(y2))

def acf_by_hand(x, lag):
    # Slice the relevant subseries based on the lag
    y1 = x[:(len(x)-lag)]
    y2 = x[lag:]
    # Subtract the mean of the whole series x to calculate Cov
    sum_product = np.sum((y1-np.mean(x))*(y2-np.mean(x)))
    # Normalize with var of whole series
    return sum_product / ((len(x) - lag) * np.var(x))

x = np.linspace(0,100,101)

results = {}
nlags=10
results["acf_by_hand"] = [acf_by_hand(x, lag) for lag in range(nlags)]
results["autocorr_by_hand"] = [autocorr_by_hand(x, lag) for lag in range(nlags)]
results["autocorr"] = [pd.Series(x).autocorr(lag) for lag in range(nlags)]
results["acf"] = acf(x, unbiased=True, nlags=nlags-1)

pd.DataFrame(results).plot(kind="bar", figsize=(10,5), grid=True)
plt.xlabel("lag")
plt.ylim([-1.2, 1.2])
plt.ylabel("value")
plt.show()

Statsmodels использует np.correlate оптимизировать это, но это в основном, как это работает.

Источник

В следующем примере Панды autocorr() функция дает ожидаемые результаты, но statmodels acf() функция не работает.

Рассмотрим следующую серию:

import pandas as pd
s = pd.Series(range(10))

Мы ожидаем, что существует идеальная корреляция между этой серией и любой из ее запаздывающих серий, и это действительно то, что мы получаем с autocorr() функция

[ s.autocorr(lag=i) for i in range(10) ]
# [0.9999999999999999, 1.0, 1.0, 1.0, 1.0, 0.9999999999999999, 1.0, 1.0, 0.9999999999999999, nan]

Но используя acf() получаем другой результат:

from statsmodels.tsa.stattools import acf
acf(s)
# [ 1.          0.7         0.41212121  0.14848485 -0.07878788 
#  -0.25757576 -0.37575758 -0.42121212 -0.38181818 -0.24545455]

Если мы попробуем acf с участием adjusted=True результат еще более неожиданный, потому что для некоторых лагов результат меньше -1 (обратите внимание, что корреляция должна быть в [-1, 1])

acf(s, adjusted=True)  # 'unbiased' is deprecated and 'adjusted' should be used instead
# [ 1.          0.77777778  0.51515152  0.21212121 -0.13131313 
#  -0.51515152 -0.93939394 -1.4040404  -1.90909091 -2.45454545]
Источник

Как предлагается в комментариях, проблему можно уменьшить, но не полностью решить, предоставив unbiased=True к statsmodels функция. Использование случайного ввода:

import statistics

import numpy as np
import pandas as pd
from statsmodels.tsa.stattools import acf

DATA_LEN = 100
N_TESTS = 100
N_LAGS = 32

def test(unbiased):
  data = pd.Series(np.random.random(DATA_LEN))
  data_acf_1 = acf(data, unbiased=unbiased, nlags=N_LAGS)
  data_acf_2 = [data.autocorr(i) for i in range(N_LAGS+1)]
  # return difference between results
  return sum(abs(data_acf_1 - data_acf_2))

for value in (False, True):
  diffs = [test(value) for _ in range(N_TESTS)]
  print(value, statistics.mean(diffs))

Выход:

False 0.464562410987
True 0.0820847168593
Источник
Другие вопросы по тегам