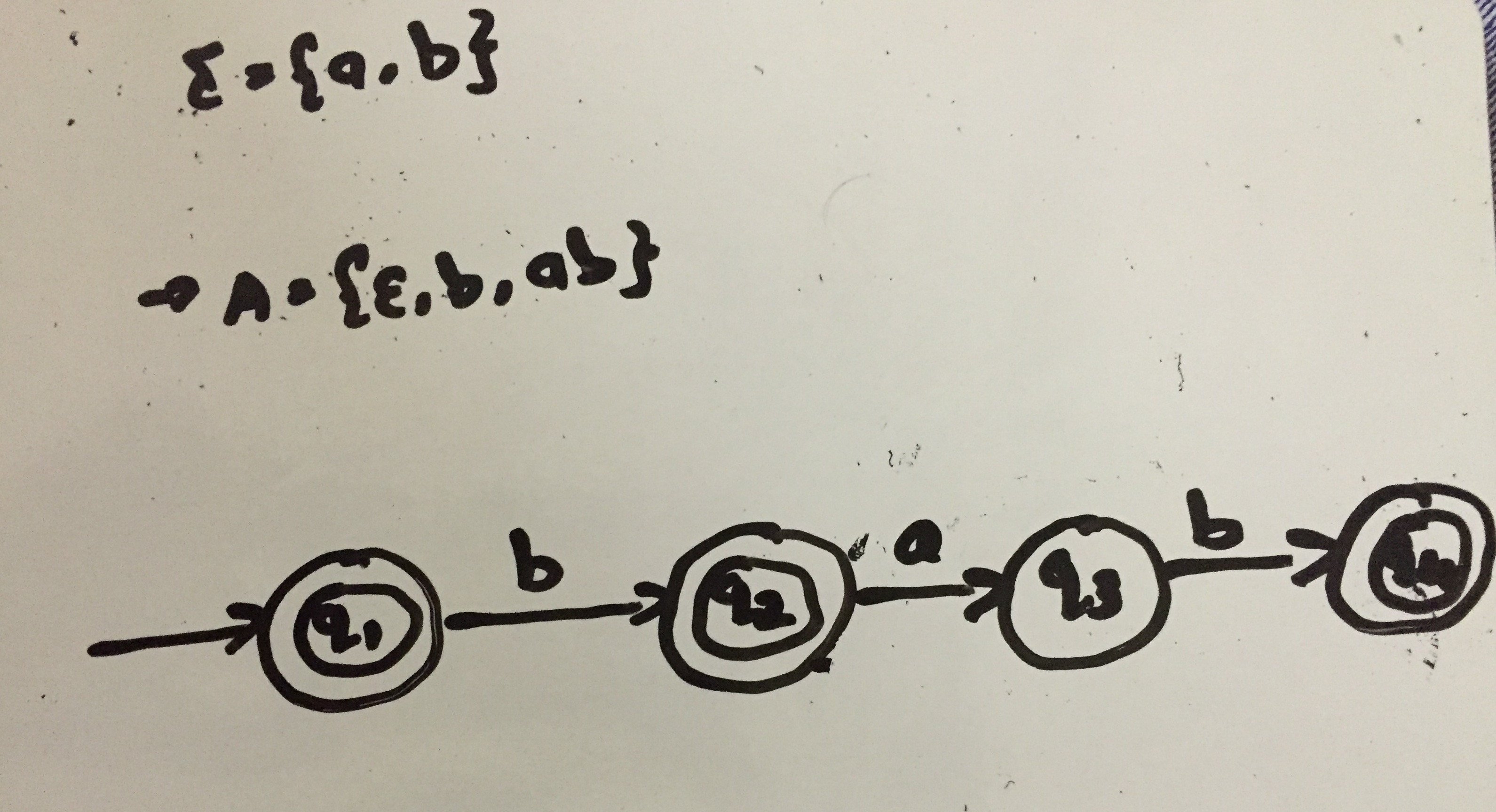Регулярное выражение в DFA

Question

Может кто-нибудь сказать мне, правильно ли подключен DFA?

Я предполагаю дать DFA для языка с алфавитом Σ ={a, b}

Мне нужен DFA для этого ----> A={ε, b, ab}

Answer 1

Нет, по нескольким причинам:

1. Твой автомат bab
2. Ваш автомат не принимает ab
3. Ваш автомат не DFA, по некоторым строгим определениям

Что касается первого пункта: начиная с q1, мы видим b, идти к q2, увидеть a, идти к q3, увидеть bи перейти к q4, который принимает. Мы видели bab и принял это.

Что касается второго пункта: начиная с q1, мы видим a но не имеют определенного перехода. Автомат "вылетает" и не принимает. Так что нет строки, начинающейся с a принято, в том числе ab,

Что касается третьего пункта: DFA часто должны показывать все состояния и переходы, включая мертвые состояния и переходы, которые никогда не приведут к какому-либо принимающему состоянию. Вы не показываете все переходы и не показывает все состояния в вашем автомате.

Вы можете использовать теорему Myhill-Nerode, чтобы определить, сколько состояний имеет минимальный DFA для вашего языка. Мы отмечаем, что к пустому состоянию можно добавить либо пустую строку, b или же ab получить строку на языке; a могу иметь b прилагается; а также b можно добавить пустую строку. Ничто не может быть добавлено к aa, bb, или же ba получить строку на языке (поэтому они неразличимы); но ab может быть добавлена ​​пустая строка (и поэтому неотличима от b).

Определенные таким образом классы эквивалентности соответствуют состояниям в минимальном DFA. Наши классы эквивалентности:

1. Строки как пустая строка
2. Строки, как b
3. Строки, как a
4. Строки, как aa

Мы отмечаем, что b на языке, поэтому второй класс будет соответствовать принимающему состоянию. Мы замечаем, что ничего не может быть добавлено к aa чтобы получить строку на языке, поэтому этот класс соответствует мертвому состоянию в DFA. Мы записываем переходы между этими состояниями, видя, в какой новый класс эквивалентности добавляется новый символ:

1. Прикрепление a ставит нас в (3) с момента добавления a пустой строке дает a который находится в (3). Прикрепление b ставит нас в (2) с момента добавления b пустой строке дает b который находится в (2)

2. Прикрепление a ставит нас в (4) с момента добавления a чтобы b дает ba который как aa в том, что это не префикс какой-либо строки в языке. Прикрепление bмы приходим в (4) по аналогичному аргументу.

3. Прикрепление a мы получаем aa и находятся в (4). Прикрепление b мы получаем ab который как b так что мы в (2).

4. Все переходы из мертвого состояния возвращаются в мертвое состояние; и то и другое a а также b вернитесь к (4).

Вы получите что-то вроде:

q1 --a--> q3
 |        /|
 b  --b--< a
 | /       |
 vv        v
q2 -a,b-> q4 \
           ^ a,b
           \_/

Или в табличной форме:

q    s    q'
==   =    ==
q1   a    q3
q1   b    q2
q2   a    q4
q2   b    q4
q3   a    q4
q3   b    q2
q4   a    q4
q4   b    q4

Answer 2

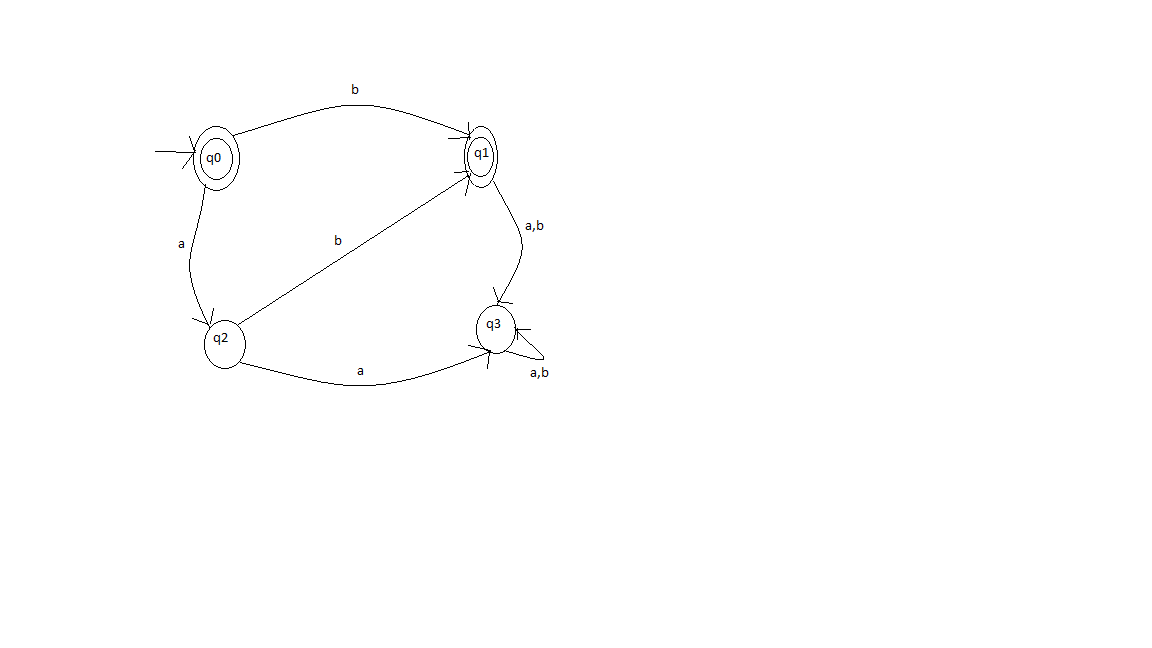
Ваш прикрепленный DFA неверен. Ваш DFA приемлем только для €,b,bab, но не может принимать ab. Чтобы ваш dfa принимал ab, также добавьте новое состояние в q0, которое принимает a, и всякий раз, когда newstate получает ввод, поскольку b отправляет его в конечное состояние. Поскольку это dfa, входы, которые вам не требуются, отправляют его в новое состояние (DEAD STATE). dfa для вашего вопроса находится здесь:нажмите здесь, чтобы просмотреть dfa

Answer 3

Я думаю, что этот DFA подходит для этого языка.