Радужный стол?
Кто-нибудь знает, почему он называется радужным столом? Только что вспомнили, что мы узнали, что есть атака, которая называется "словарная атака". Почему это не называется словарь?
4 ответа
Потому что он содержит весь "спектр" возможностей.
Атака по словарю - это грубая техника просто пробных возможностей. Вот так (псевдокод Python)
mypassworddict = dict()
for password in mypassworddict:
trypassword(password)
Однако радужный стол работает по-другому, потому что он предназначен для инвертирования хешей. Общий обзор хэша состоит в том, что он имеет несколько бинов:
bin1, bin2, bin3, bin4, bin5, ...
Которые соответствуют бинарным частям выходной строки - так строка заканчивается в длину. По мере продолжения хэша он по-разному влияет на разные части бинов. Таким образом, первый байт (или любое другое входное поле принимается) влияет на (скажем, упрощенно) элементы 3 и 4. Следующий вход влияет на 2 и 6. И так далее.
Радужная таблица - это вычисление всех возможностей данного бина, то есть всех возможных инверсий этого бина, для каждого бина... вот почему он так велик. Если первое значение bin 0x1 тогда вам нужно иметь список поиска всех значений bin2 и все значения bin3 работают в обратном направлении через хеш, который в конечном итоге дает вам значение.
Почему это не называется атакой по словарю? Потому что это не так.
Как я уже видел ваш предыдущий вопрос, позвольте мне подробнее остановиться на деталях, которые вы там ищете. Криптографически безопасный хеш должен быть идеально защищен от небольших входных размеров до целых файлов. Предварительное вычисление значений хеша для всего файла заняло бы вечность. Таким образом, радужная таблица разработана на небольшом хорошо понятном подмножестве выходных данных, например, перестановки всех символов az над полем, скажем, 10 символов.
Вот почему совет по паролю для победы над атаками по словарям работает здесь. Чем больше подмножеств всего возможного набора входных данных, которые вы вводите в свой ввод для хэша, тем больше радуговой таблицы должно содержаться для его поиска. Требуемые размеры данных оказываются глупо большими, как и время поиска. Итак, подумайте об этом:
- Если у вас есть вход, который
[a-z]за5-8персонажи, это не так уж плохо для радужного стола. - Если вы увеличите длину до 42 символов, это будет огромный радужный стол. Каждый вход влияет на хеш и, следовательно, на ячейки указанного хеша.
- Если вы добавляете цифры к вашему запросу
[a-z][0-9]у вас есть еще больше поисков, чтобы сделать. - также
[A-Za-z0-9], Наконец, придерживайтесь[\w]то есть любой печатный персонаж, о котором вы можете подумать, и опять же, вы смотрите на массивный стол.
Таким образом, из-за длинных и сложных паролей радужные таблицы начинают принимать диски данных размером с синий луч. Затем, в соответствии с вашим предыдущим вопросом, вы начинаете добавлять функции, основанные на солении и хэше, и принимаете общее решение для хэширования (er).
Цель здесь - опередить имеющиеся вычислительные мощности.
Rainbow - это вариант атаки по словарю (точнее, заранее рассчитанная атака по словарю), но она занимает меньше места, чем полный словарь (ценой времени, необходимого для поиска ключа в таблице). Другим концом этого компромисса между пространством и памятью является полный поиск (атака методом грубой силы = нулевое предварительное вычисление, много времени).
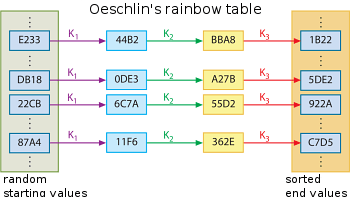
В радужной таблице предварительно вычисленный словарь пар ключ-шифротекст сжимается в цепочки. Каждый шаг в цепочке выполняется с использованием разных функций сжатия. А на столе много цепей, поэтому он выглядит как радуга.
На этом рисунке разные функции сжатия K1, K2, K3 имеют цвета, похожие на радугу: таблица, хранящаяся в файле, содержит только первый и последний столбцы, поскольку средние столбцы можно пересчитать.
К сожалению, некоторые из утверждений не верны. Вопреки тому, что приносят опубликованные радужные таблицы, НЕ содержат все возможности для данного пространства ключей, а не те, которые созданы для использования, которое я видел. Они могут быть сгенерированы для покрытия 99,9, но из-за случайности хэш-функции нет никакой гарантии, что КАЖДЫЙ открытый текст будет покрыт.
Каждая цепочка состоит из звеньев или шагов, а каждый шаг состоит из функции хеширования и редукции. Если бы ваша цепочка была длиной 100 ссылок, вы бы пошли на это число функций хеширования / редукции, а затем отбросили бы все промежуточное, кроме начала и конца.
Чтобы найти простой для заданного хеша, вы просто выполняете уменьшение / хеш х длины вашей цепочки. Таким образом, вы выполняете шаг один раз и проверяете конечную точку, не пропустите ли вы промах... Пока вы не пройдете всю длину своей цепи. Если есть совпадение, вы можете восстановить цепь с начальной точки, и вы сможете найти равнину. Если после регенерации это не правильно, то это ложная тревога. Это происходит из-за столкновений, вызванных уменьшением хэш-функции. Так как таблица содержит много цепочек, вы можете выполнять большой поиск по всем конечным точкам цепочки на каждом шаге, это, по сути, магия, которая позволяет скорость. Это также приведет к ложным тревогам, поскольку вам нужно только восстанавливать цепочки, у которых есть совпадения, вы экономите много времени, пропуская ненужные цепочки.
Они не содержат словарей.... Ну, а не традиционные таблицы, есть варианты радужных таблиц, которые включают использование словарей.
Вот и все. Есть много способов, которыми этот процесс был оптимизирован, включая удаление объединяющих / дублирующих цепочек и создание идеальных таблиц, а также хранение их в разных упаковках для экономии места и времени загрузки.
Я не знаю, откуда пришло название, но есть различия:
- Словарь содержит несколько выбранных элементов (например, английские слова), а радужная таблица содержит все возможные комбинации.
- Словарь содержит только входные данные, тогда как радужная таблица содержит как входные, так и выходные данные.
- Словарь используется для проверки различных входных данных, чтобы убедиться, что выходные данные действительны, в то время как радужная таблица используется для обратного просмотра, т. Е. Чтобы найти, какой вход дает конкретный выход.