Как создать объем из облака точек в сферических координатах?

Question

У меня есть два набора дискретных точек в сферических координатах, каждый из которых представляет верхнюю и нижнюю поверхности объекта.

Я пытаюсь создать объем из этих точек, чтобы отделить точки, которые лежат внутри и снаружи объекта. Любые предложения, где искать или какую библиотеку использовать?

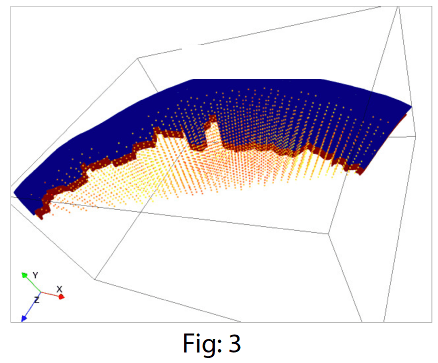
Синие и красные точки представляют верхнюю и нижнюю поверхности. Красные точки создаются путем смещения верхней поверхности радиально вниз с постоянным радиусом.

Answer 1

Если я прав, синие и красные поверхности зашиты (и водонепроницаемы). Таким образом, для каждой точки вы можете нарисовать линию от центра сферы и искать пересечения с сеткой. Это делается путем нахождения двух треугольников таким образом, чтобы линия проходила через них (это можно сделать, просматривая только угловые координаты, используя формулу точка-треугольник), а затем находя точки пересечения. Тогда легко классифицировать точку как перед красной поверхностью, после синей или между ними.

Исчерпывающий поиск треугольников может быть дорогостоящим. Вы можете ускорить его, например, используя иерархию ограничивающих рамок или подобное устройство.

Answer 2

Вот пользовательский метод сшивки, который может работать при условии, что среднее расстояние между точками на исходной поверхности намного меньше толщины объема и неровностей на контуре поверхности. Другими словами, что есть много точек, описывающих синие поверхности.

import matplotlib.pylab as plt

import numpy as np
from scipy.spatial import KDTree

# Generate a test surface:
theta = np.linspace(3, 1, 38)
phi = np.zeros_like(theta)
r = 1 + 0.1*np.sin(8*theta)

surface_points = np.stack((r, theta, phi), axis=1)  #  n x 3 array

# Generate test points:
x_span, y_span = np.linspace(-1, 0.7, 26), np.linspace(0.1, 1.2, 22)
x_grid, y_grid = np.meshgrid(x_span, y_span)

r_test = np.sqrt(x_grid**2 + y_grid**2).ravel()
theta_test = np.arctan2(y_grid, x_grid).ravel()
phi_test = np.zeros_like(theta_test)

test_points = np.stack((r_test, theta_test, phi_test), axis=1)  #  n x 3 array

# Determine if the test points are in the volume:

volume_thickness = 0.2  # Distance between the two surfaces
angle_threshold = 0.05  # Angular threshold to determine for a point 
                        # if the line from the origin to the point 
                        # go through the surface

# Get the nearest point: (replace the interpolation)
get_nearest_points = KDTree(surface_points[:, 1:]) # keep only the angles
# This is based on the cartesian distance,
# and therefore not enterily valid for the angle between points on a sphere
# It could be better to project the points on a unit shpere, and convert 
# all coordinates in cartesian frame in order to do the nearest point seach...

distance, idx = get_nearest_points.query(test_points[:, 1:])

go_through = distance < angle_threshold

nearest_surface_radius = surface_points[idx, 0]

is_in_volume = (go_through) & (nearest_surface_radius > test_points[:, 0]) \
                & (nearest_surface_radius - volume_thickness < test_points[:, 0])

not_in_volume = np.logical_not(is_in_volume)

# Graph;
plt.figure(figsize=(10, 7))
plt.polar(test_points[is_in_volume, 1], test_points[is_in_volume, 0], '.r',
          label='in volume');
plt.polar(test_points[not_in_volume, 1], test_points[not_in_volume, 0], '.k',
          label='not in volume', alpha=0.2);
plt.polar(test_points[go_through, 1], test_points[go_through, 0], '.g',
          label='go through', alpha=0.2);
plt.polar(surface_points[:, 1], surface_points[:, 0], '.b',
          label='surface');
plt.xlim([0, np.pi]); plt.grid(False);plt.legend();

График результатов для 2D-случая:

Идея состоит в том, чтобы искать каждую контрольную точку ближайшую точку на поверхности, учитывая только направление, а не радиус. Как только эта точка "того же направления" найдена, можно проверить оба, находится ли точка внутри объема вдоль радиального направления (volume_thickness) и достаточно близко к поверхности, используя параметр angle_threshold,

Я думаю, что было бы лучше создать сетку (не выпуклую) синей поверхности и выполнить правильную интерполяцию, но я не знаю метода Сципи для этого.