Как я могу выполнить двумерную интерполяцию с помощью Scipy?

Question

Этот Q&A предназначен как канонический (-ish) относительно двумерной (и многомерной) интерполяции с использованием scipy. Часто возникают вопросы, касающиеся базового синтаксиса различных многомерных методов интерполяции, я надеюсь, что они тоже будут ясны.

У меня есть набор рассеянных двумерных точек данных, и я хотел бы нарисовать их как красивую поверхность, предпочтительно используя что-то вроде contourf или же plot_surface в matplotlib.pyplot, Как я могу интерполировать свои двумерные или многомерные данные в сетку, используя scipy?

Я нашел scipy.interpolate субпакет, но я получаю ошибки при использовании interp2d или же bisplrep или же griddata или же rbf, Каков правильный синтаксис этих методов?

Answer 1

Отказ от ответственности: я в основном пишу этот пост с учетом синтаксических соображений и общего поведения. Я не знаком с аспектом памяти и ЦП описанных методов, и я нацеливаю этот ответ на тех, у кого достаточно небольшие наборы данных, так что качество интерполяции может быть основным аспектом, который следует учитывать. Я знаю, что при работе с очень большими наборами данных, более эффективные методы (а именно griddata а также Rbf) может быть неосуществимым.

Я собираюсь сравнить три вида многомерных методов интерполяции (interp2d / шлицы, griddata а также Rbf). Я буду подвергать их двум видам интерполяционных задач и двум видам базовых функций (точки, из которых нужно интерполировать). Конкретные примеры будут демонстрировать двумерную интерполяцию, но жизнеспособные методы применимы в произвольных измерениях. Каждый метод обеспечивает различные виды интерполяции; во всех случаях я буду использовать кубическую интерполяцию (или что-то близкое к ¹). Важно отметить, что всякий раз, когда вы используете интерполяцию, вы вносите смещение по сравнению с вашими необработанными данными, и конкретные используемые методы влияют на артефакты, которые у вас получатся. Всегда помните об этом и выполняйте ответственно.

Две задачи интерполяции будут

1. повышающая дискретизация (входные данные на прямоугольной сетке, выходные данные на более плотной сетке)
2. интерполяция разбросанных данных на регулярную сетку

Две функции (над доменом [x,y] in [-1,1]x[-1,1]) будет

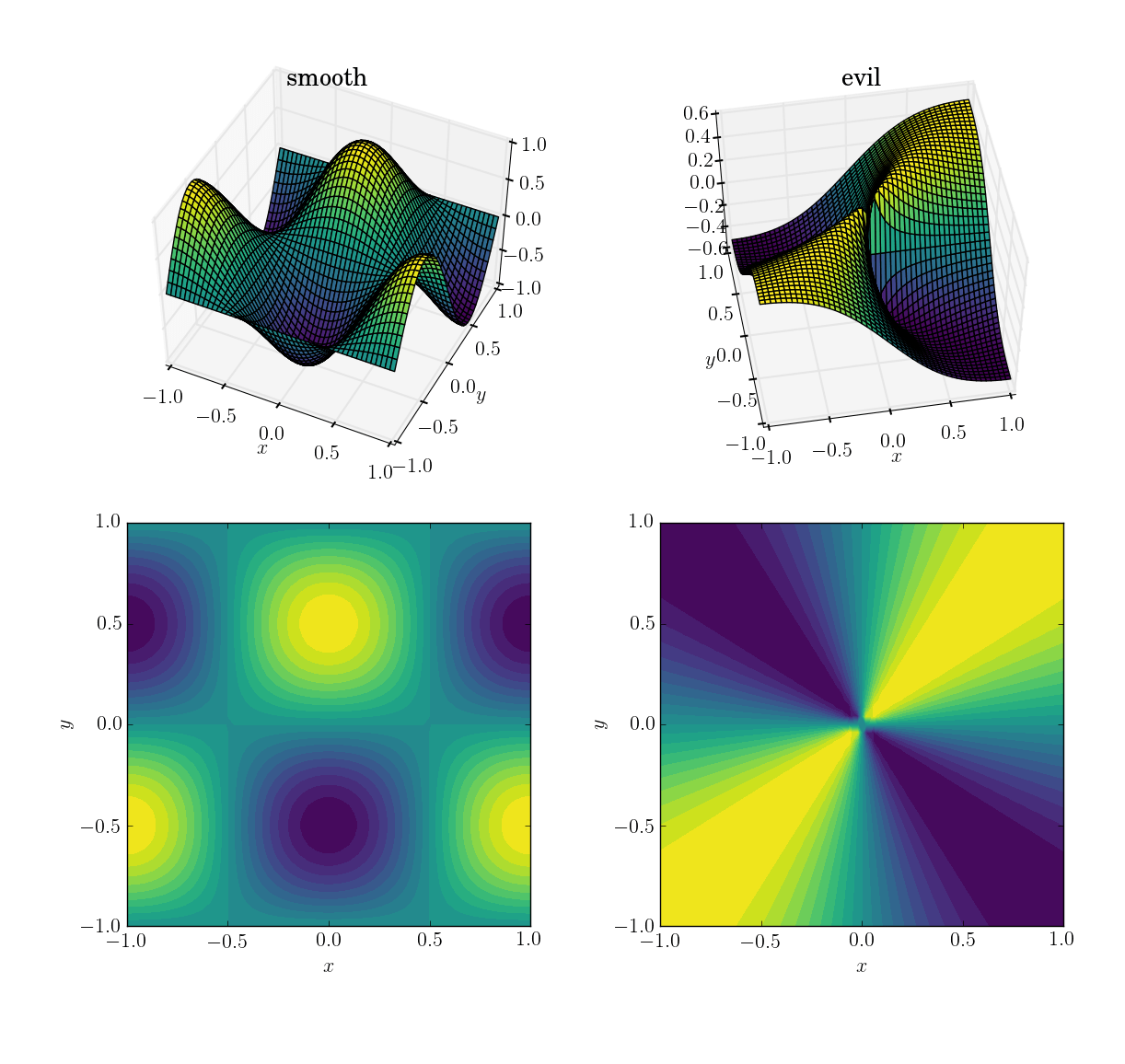
1. гладкая и дружелюбная функция: cos(pi*x)*sin(pi*y); диапазон в [-1, 1]
2. злая (и, в частности, не непрерывная) функция: x*y/(x^2+y^2) со значением 0,5 около начала координат; диапазон в [-0.5, 0.5]

Вот как они выглядят:

Сначала я покажу, как эти три метода ведут себя в рамках этих четырех тестов, а затем подробно опишу синтаксис всех трех. Если вы знаете, чего ожидать от метода, вы можете не тратить время на изучение его синтаксиса (глядя на вас, interp2d).

Тестовые данные

Для ясности, вот код, с помощью которого я сгенерировал входные данные. Хотя в этом конкретном случае я, очевидно, осведомлен о функции, лежащей в основе данных, я буду использовать ее только для генерации входных данных для методов интерполяции. Я использую numpy для удобства (и в основном для генерации данных), но одного scipy тоже будет достаточно.

import numpy as np
import scipy.interpolate as interp

# auxiliary function for mesh generation
def gimme_mesh(n):
    minval = -1
    maxval =  1
    # produce an asymmetric shape in order to catch issues with transpositions
    return np.meshgrid(np.linspace(minval,maxval,n), np.linspace(minval,maxval,n+1))

# set up underlying test functions, vectorized
def fun_smooth(x, y):
    return np.cos(np.pi*x)*np.sin(np.pi*y)

def fun_evil(x, y):
    # watch out for singular origin; function has no unique limit there
    return np.where(x**2+y**2>1e-10, x*y/(x**2+y**2), 0.5)

# sparse input mesh, 6x7 in shape
N_sparse = 6
x_sparse,y_sparse = gimme_mesh(N_sparse)
z_sparse_smooth = fun_smooth(x_sparse, y_sparse)
z_sparse_evil = fun_evil(x_sparse, y_sparse)

# scattered input points, 10^2 altogether (shape (100,))
N_scattered = 10
x_scattered,y_scattered = np.random.rand(2,N_scattered**2)*2 - 1
z_scattered_smooth = fun_smooth(x_scattered, y_scattered)
z_scattered_evil = fun_evil(x_scattered, y_scattered)

# dense output mesh, 20x21 in shape
N_dense = 20
x_dense,y_dense = gimme_mesh(N_dense)

Гладкая функция и повышающая дискретизация

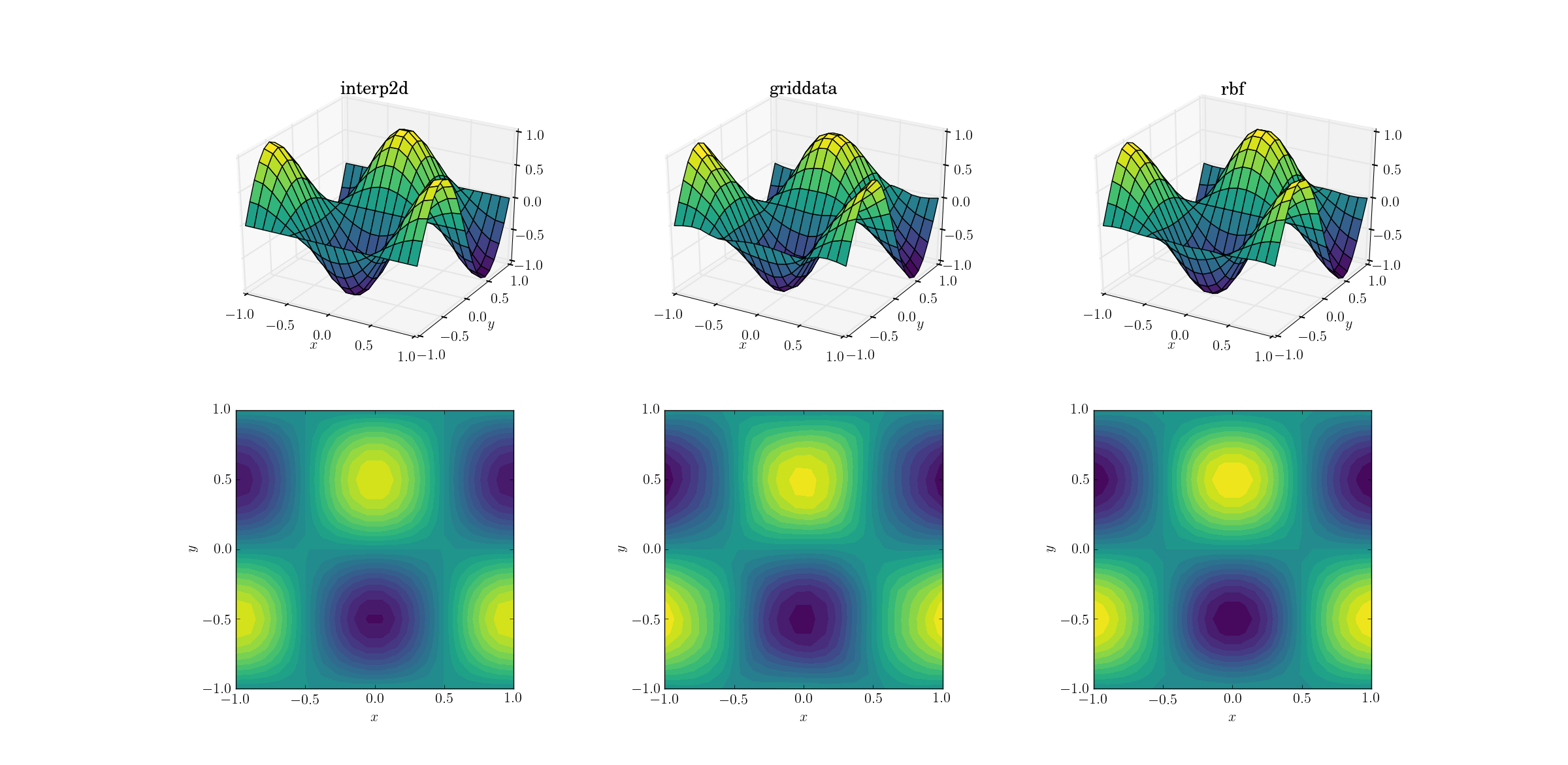
Давайте начнем с самой простой задачи. Вот как повышается выборка из сетки формы [6,7] одному из [20,21] работает для гладкой тестовой функции:

Даже если это простая задача, между выходами уже есть тонкие различия. На первый взгляд все три выхода являются разумными. Следует обратить внимание на две особенности, основанные на наших предыдущих знаниях основной функции: средний случай griddata искажает данные больше всего. Обратите внимание y==-1 граница участка (ближайшая к x label): функция должна быть строго нулевой (поскольку y==-1 является узловой линией для гладкой функции), но это не так для griddata, Также обратите внимание на x==-1 Граница графиков (сзади, слева): основная функция имеет локальный максимум (подразумевающий нулевой градиент вблизи границы) в [-1, -0.5], но griddata Выходные данные показывают явно ненулевой градиент в этой области. Эффект незаметен, но, тем не менее, это предвзятость. (Верность Rbf еще лучше с выбором по умолчанию радиальных функций, дублированных multiquadratic.)

Злая функция и повышающая выборка

Немного более трудная задача состоит в том, чтобы выполнить повышающую дискретизацию нашей злой функции:

Четкие различия начинают проявляться среди трех методов. Глядя на поверхностные графики, на выходе из явных ложных экстремумов появляются interp2d (обратите внимание на два горба на правой стороне нанесенной поверхности). В то время как griddata а также Rbf с первого взгляда, похоже, дают схожие результаты, последний, по-видимому, дает более глубокий минимум [0.4, -0.4] это отсутствует в основной функции.

Тем не менее, есть один важный аспект, в котором Rbf намного превосходит: он учитывает симметрию базовой функции (что, конечно, также стало возможным благодаря симметрии выборочной сетки). Выход из griddata нарушает симметрию точек выборки, что уже слабо видно в гладком случае.

Гладкая функция и разбросанные данные

Чаще всего нужно выполнить интерполяцию на разбросанных данных. По этой причине я ожидаю, что эти тесты будут более важными. Как показано выше, точки выборки были выбраны псевдооднородно в интересующей области. В реалистичных сценариях у вас может быть дополнительный шум при каждом измерении, и вы должны подумать, имеет ли смысл для начала интерполировать ваши исходные данные.

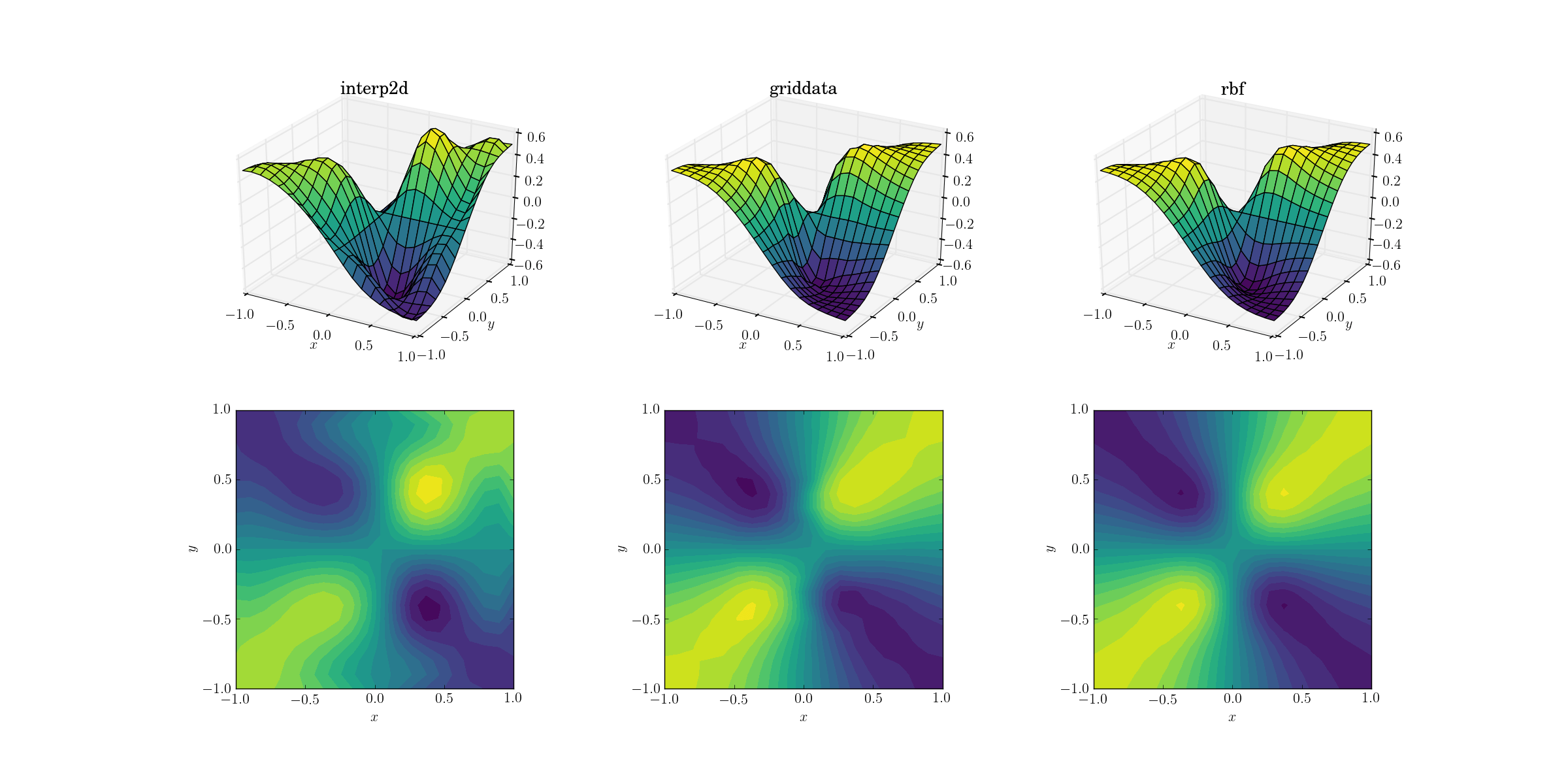
Выход для гладкой функции:

Сейчас уже идет ужасное шоу. Я обрезал вывод из interp2d между [-1, 1] исключительно для построения графиков, чтобы сохранить хотя бы минимальное количество информации. Понятно, что, хотя некоторые из основных форм присутствуют, есть огромные шумные области, где метод полностью выходит из строя. Второй случай griddata довольно хорошо воспроизводит форму, но обратите внимание на белые области на границе контурного графика. Это связано с тем, что griddata работает только внутри выпуклой оболочки точек входных данных (другими словами, он не выполняет никакой экстраполяции). Я сохранил значение NaN по умолчанию для выходных точек, лежащих вне выпуклой оболочки. ² Учитывая эти особенности, Rbf кажется, работает лучше всего.

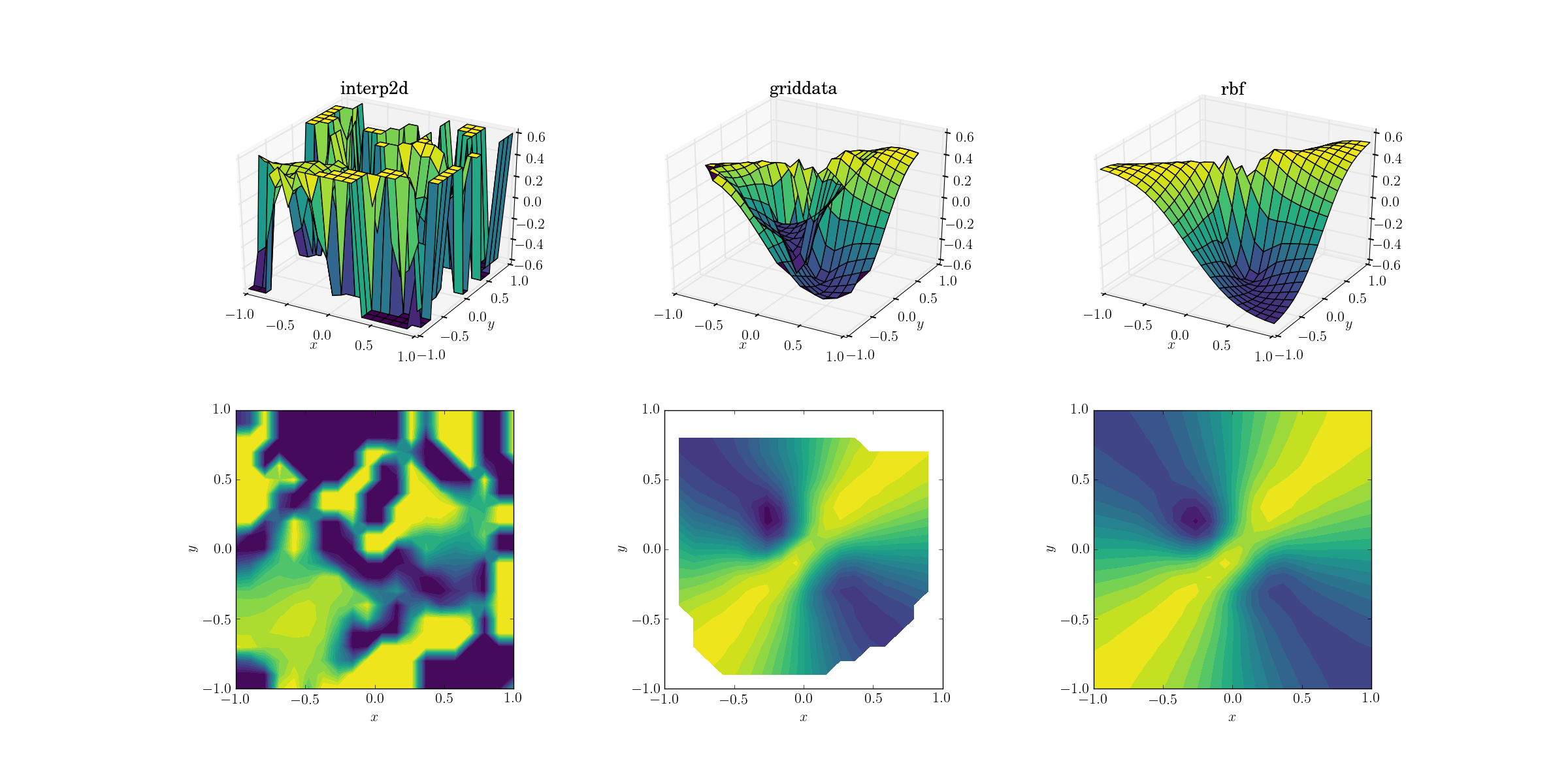
Злая функция и разбросанные данные

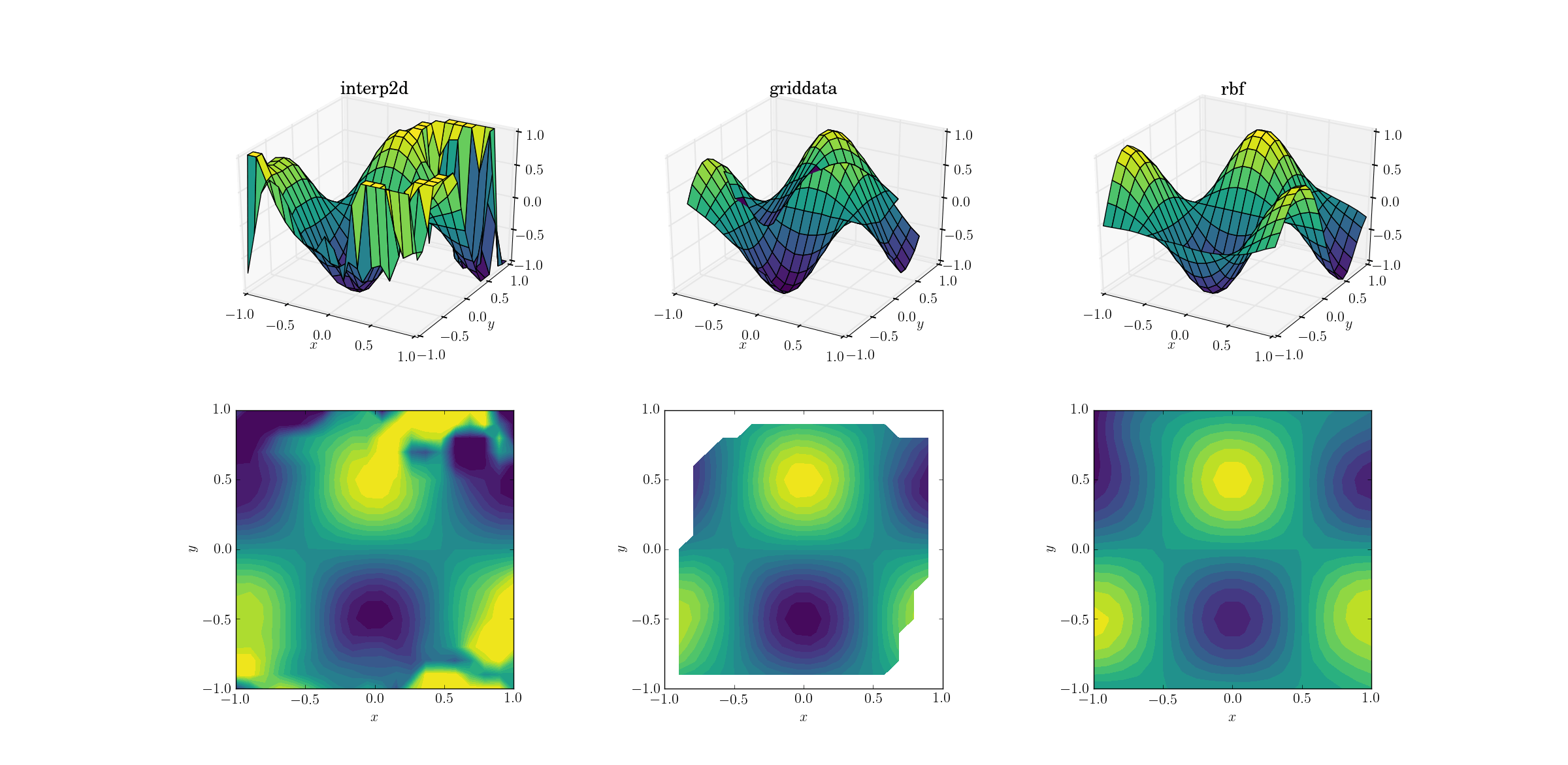
И момент, которого мы все ждали:

Не удивительно, что interp2d сдается. На самом деле, во время звонка interp2d вам стоит ожидать дружелюбия RuntimeWarning s жалуются на невозможность построения сплайна. Что касается двух других методов, Rbf кажется, дает лучший результат, даже вблизи границ домена, где результат экстраполируется.

---

Итак, позвольте мне сказать несколько слов о трех методах, в порядке убывания предпочтения (чтобы наихудший из всех читал наименьшую вероятность).

scipy.interpolate.Rbf

Rbf класс расшифровывается как "радиальные базисные функции". Честно говоря, я никогда не рассматривал этот подход, пока не начал исследовать этот пост, но я уверен, что буду использовать их в будущем.

Как и сплайн-методы (см. Далее), использование происходит в два этапа: первый создает вызываемый Rbf Экземпляр класса на основе входных данных, а затем вызывает этот объект для заданной выходной сетки для получения интерполированного результата. Пример из теста сглаживания с повышением частоты:

import scipy.interpolate as interp
zfun_smooth_rbf = interp.Rbf(x_sparse, y_sparse, z_sparse_smooth, function='cubic', smooth=0)  # default smooth=0 for interpolation
z_dense_smooth_rbf = zfun_smooth_rbf(x_dense, y_dense)  # not really a function, but a callable class instance

Обратите внимание, что в этом случае точки входа и выхода были 2d массивами, а выходные z_dense_smooth_rbf имеет ту же форму, что и x_dense а также y_dense без каких-либо усилий. Также обратите внимание, что Rbf поддерживает произвольные размеры для интерполяции.

Так, scipy.interpolate.Rbf

• производит хороший вывод даже для сумасшедших входных данных
• поддерживает интерполяцию в более высоких измерениях
• Экстраполяция вне выпуклой оболочки входных точек (конечно, экстраполяция - это всегда игра, и вы вообще не должны на нее полагаться)
• создает интерполятор в качестве первого шага, поэтому оценка его в различных выходных точках требует меньших дополнительных усилий
• может иметь выходные точки произвольной формы (в отличие от прямоугольных ячеек, см. позже)
• склонен к сохранению симметрии входных данных
• поддерживает несколько видов радиальных функций для ключевого слова function: multiquadric, inverse, gaussian, linear, cubic, quintic, thin_plate и пользовательский произвольный

scipy.interpolate.griddata

Мой бывший любимый, griddata является общей рабочей лошадкой для интерполяции в произвольных измерениях. Он не выполняет экстраполяцию, кроме установки единственного заданного значения для точек за пределами выпуклой оболочки узловых точек, но, поскольку экстраполяция - очень непостоянная и опасная вещь, это не обязательно мошенничество. Пример использования:

z_dense_smooth_griddata = interp.griddata(np.array([x_sparse.ravel(),y_sparse.ravel()]).T,
                                          z_sparse_smooth.ravel(),
                                          (x_dense,y_dense), method='cubic')   # default method is linear

Обратите внимание на слегка неаккуратный синтаксис. Точки ввода должны быть указаны в виде массива [N, D] в D размеры. Для этого мы сначала должны сгладить наши 2d координатные массивы (используя ravel), затем объединить массивы и транспонировать результат. Есть несколько способов сделать это, но все они кажутся громоздкими. Вход z данные также должны быть сведены. У нас есть немного больше свободы, когда дело доходит до выходных точек: по некоторым причинам они также могут быть определены как кортеж многомерных массивов. Обратите внимание, что help из griddata вводит в заблуждение, поскольку предполагает, что то же самое верно для точек ввода (по крайней мере, для версии 0.17.0):

griddata(points, values, xi, method='linear', fill_value=nan, rescale=False)
    Interpolate unstructured D-dimensional data.

    Parameters
    ----------
    points : ndarray of floats, shape (n, D)
        Data point coordinates. Can either be an array of
        shape (n, D), or a tuple of `ndim` arrays.
    values : ndarray of float or complex, shape (n,)
        Data values.
    xi : ndarray of float, shape (M, D)
        Points at which to interpolate data.

В двух словах, scipy.interpolate.griddata

• производит хороший вывод даже для сумасшедших входных данных
• поддерживает интерполяцию в более высоких измерениях
• не выполняет экстраполяцию, одно значение может быть установлено для выхода за пределы выпуклой оболочки входных точек (см. fill_value)
• вычисляет интерполированные значения в одном вызове, поэтому поиск нескольких наборов выходных точек начинается с нуля
• может иметь выходные точки произвольной формы
• поддерживает ближнюю и линейную интерполяцию в произвольных измерениях, кубическая в 1d и 2d. Использование ближайшего соседа и линейная интерполяция NearestNDInterpolator а также LinearNDInterpolator под капотом соответственно. 1d кубическая интерполяция использует сплайн, 2d кубическая интерполяция использует CloughTocher2DInterpolator построить непрерывно дифференцируемый кусочно-кубический интерполятор.
• может нарушить симметрию входных данных

scipy.interpolate.interp2d / scipy.interpolate.bisplrep

Единственная причина, по которой я обсуждаю interp2d и его родственники в том, что у него есть обманчивое имя, и люди, вероятно, попытаются использовать его. Оповещение о спойлере: не используйте его (начиная с версии scipy 0.17.0). Он уже более особенный, чем предыдущие предметы, поскольку он специально используется для двумерной интерполяции, но я подозреваю, что это, безусловно, самый распространенный случай для многомерной интерполяции.

Что касается синтаксиса, interp2d похож на Rbf тем, что сначала необходимо создать экземпляр интерполяции, который может быть вызван для предоставления фактических интерполированных значений. Однако здесь есть одна загвоздка: выходные точки должны быть расположены на прямоугольной сетке, поэтому входные данные, входящие в вызов интерполятора, должны быть 1d-векторами, которые охватывают выходную сетку, как будто из numpy.meshgrid:

# reminder: x_sparse and y_sparse are of shape [6, 7] from numpy.meshgrid
zfun_smooth_interp2d = interp.interp2d(x_sparse, y_sparse, z_sparse_smooth, kind='cubic')   # default kind is 'linear'
# reminder: x_dense and y_dense are of shape [20, 21] from numpy.meshgrid
xvec = x_dense[0,:] # 1d array of unique x values, 20 elements
yvec = y_dense[:,0] # 1d array of unique y values, 21 elements
z_dense_smooth_interp2d = zfun_smooth_interp2d(xvec,yvec)   # output is [20, 21]-shaped array

Одна из самых распространенных ошибок при использовании interp2d помещает ваши полные 2d сетки в вызов интерполяции, что приводит к взрывному потреблению памяти, и, надеюсь, к поспешному MemoryError,

Теперь самая большая проблема с interp2d в том, что это часто не работает. Чтобы понять это, нужно заглянуть под капот. Оказывается, что interp2d это обертка для функций нижнего уровня bisplrep + bisplev, которые, в свою очередь, являются обертками для подпрограмм FITPACK (написано на Фортране). Эквивалентный вызов предыдущему примеру будет

kind = 'cubic'
if kind=='linear':
    kx=ky=1
elif kind=='cubic':
    kx=ky=3
elif kind=='quintic':
    kx=ky=5
# bisplrep constructs a spline representation, bisplev evaluates the spline at given points
bisp_smooth = interp.bisplrep(x_sparse.ravel(),y_sparse.ravel(),z_sparse_smooth.ravel(),kx=kx,ky=ky,s=0)
z_dense_smooth_bisplrep = interp.bisplev(xvec,yvec,bisp_smooth).T  # note the transpose

Теперь вот вещь о interp2d: (в версии scipy 0.17.0) есть хороший комментарий в interpolate/interpolate.py за interp2d:

if not rectangular_grid:
    # TODO: surfit is really not meant for interpolation!
    self.tck = fitpack.bisplrep(x, y, z, kx=kx, ky=ky, s=0.0)

и действительно в interpolate/fitpack.py, в bisplrep есть некоторые настройки и в конечном итоге

tx, ty, c, o = _fitpack._surfit(x, y, z, w, xb, xe, yb, ye, kx, ky,
                                task, s, eps, tx, ty, nxest, nyest,
                                wrk, lwrk1, lwrk2)                 

И это все. Подпрограммы, лежащие в основе interp2d на самом деле не предназначены для выполнения интерполяции. Их может быть достаточно для достаточно хороших данных, но в реальных условиях вам, вероятно, захочется использовать что-то еще.

Просто чтобы заключить, interpolate.interp2d

• может привести к появлению артефактов даже при наличии умеренных данных
• специально для двумерных проблем (хотя есть ограниченное interpn для точек ввода, определенных на сетке)
• выполняет экстраполяцию
• создает интерполятор в качестве первого шага, поэтому оценка его в различных выходных точках требует меньших дополнительных усилий
• может производить вывод только по прямоугольной сетке, для рассеянного вывода вам придется вызывать интерполятор в цикле
• поддерживает линейную, кубическую и квинтическую интерполяцию
• может нарушить симметрию входных данных

---

¹ Я уверен, что cubic а также linear вид базисных функций Rbf не точно соответствуют другим интерполяторам с тем же именем.
² Эти NaN также являются причиной того, почему поверхностный график кажется таким странным: у matplotlib исторически возникают трудности с построением сложных трехмерных объектов с надлежащей информацией о глубине. Значения NaN в данных приводят в замешательство средство визуализации, поэтому части поверхности, которые должны быть сзади, нанесены так, чтобы быть спереди. Это проблема визуализации, а не интерполяции.