Использование MATLAB для нахождения минимаксной полиномиальной аппроксимации тригонометрических функций

Question

Я пытаюсь найти минимаксную полиномиальную аппроксимацию для синуса и косинуса, используя алгоритм обмена памяти в MATLAB. Необходима точность до 23 бит, потому что я реализую функции синуса и косинуса для плавающей запятой IEEE-754.

Используя эту ссылку здесь (см. Страницы с 8 по 15), даются инструкции по поиску полинома с использованием Mathematica и Maple, однако я не уверен, как экстраполировать эти методы для MATLAB.

В соответствии с таблицей 3 мне нужно использовать полином 5-го или 6-го порядка, чтобы получить ~23 бита (после десятичной запятой) точности.

Я планирую сначала выполнить уменьшение диапазона всех входящих тэта до уровня от -pi/4 до +pi/4, а затем выполнить функцию синуса или косинуса по мере необходимости (конечная цель - реализовать exp(i*x) = cos(х) + я * грех (х).

Я мог бы сам следовать инструкциям этой статьи, но я не знаю, как использовать функцию запоминания для моих целей здесь. Кроме того, я не понимаю, почему автор использовал уравнение (6) (на странице 9), и я не понимаю, как было определено уравнение для k (на странице 11) (откуда берется 2796201?) И почему определение форму полинома мы хотим в конечном итоге изменить на sin9x) = x + kx^3 + x^5*P(x^2).

Было бы лучше использовать вместо этого функцию firpm (так как запоминается как устаревший)?

Спасибо, вся помощь и руководство очень ценится, а также правки, чтобы обеспечить лучший ответ на мой вопрос.

Answer 1

Я бы не стал пытаться разработать собственные аппроксимации. Проще взять копию "Компьютерные аппроксимации", Харт и др. У хорошей университетской библиотеки должно быть это. 23 бита - это около 7 десятичных цифр, поэтому просто выберите приближение, которое даст вам необходимую точность. Вы можете выбрать либо простое полиномиальное приближение, либо использовать рациональный полином, обычно немного лучше, если вы можете терпеть это деление.

Уменьшение диапазона имеет смысл, на самом деле, я выбрал тот же диапазон (+/-pi/4) в моих собственных инструментах, потому что с этим выбором диапазона особенно легко работать.

Изменить: (Пример использования приближений можно найти в Харте.)

Здесь я найду приближение для sin(x), где x лежит в интервале [0,pi/4]. Моя цель состоит в том, чтобы выбрать аппроксимацию с абсолютной точностью не менее 1.e-7 на этом интервале. Конечно, если у вас есть отрицательное значение для x, мы знаем, что sin (x) является нечетной функцией, так что это тривиально.

Отмечу, что приближения в Харте имеют тенденцию иметь форму sin (alphapi x), где x лежит в интервале [0,1]. Если бы я затем выбрал приближение для альфа = 1/2, я бы получил приближение, которое действует в течение выбранного интервала. Таким образом, для аппроксимации на интервале [0, pi / 4] мы ищем альфа = 1/4.

Далее, я ищу приближение, которое, как указано, имеет абсолютную точность не менее 7 цифр или около того, и я предпочитаю использовать рациональные полиномиальные приближения, поскольку они имеют тенденцию быть немного более эффективными. Сканируя таблицы на странице 118 (моя копия Харта с 1978 года), я нахожу приближение с альфа = 1/4, которое соответствует счету: индекс 3060.

Это приближение будет иметь вид

sin(alpha*pi*x) = x*P(x^2)/Q(x^2)

Итак, теперь я перехожу на страницу, которая дает коэффициенты для SIN 3060. В моем экземпляре она находится на страницах 199-200. Есть 5 коэффициентов, P00, P01, P02, Q00, Q01. (Следите за несколько нестандартными научными обозначениями, используемыми здесь.) Таким образом, P (полином числителя) содержит 3 члена, а Q, знаменатель имеет 2 члена. Записав это, я получаю это:

sin(alpha*pi*x) = (52.81860134812 -4.644800481954*x^3 + 0.0867545069521*x^5)/ ...
    (67.250731777791 + x^2)

Давайте попробуем это сейчас в MATLAB.

x = linspace(0,pi/4,10001);
xt = x*4/pi; % transform to [0,1]
sine = @(x) (52.81860134812*x -4.644800481954*x.^3 + ...
     0.0867545069521*x.^5)./(67.250731777791 + x.^2);

max(abs(sin(x) -sine(xt)))
ans =
   1.6424e-09

plot(x,sin(x)- sine(xt),'-')

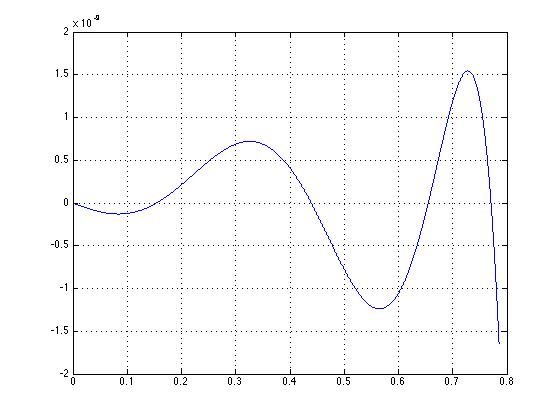
Обратите внимание на 1e-9, прикрепленный к оси Y.

Похоже, что это наиболее разумный выбор аппроксимации для sin (x) в этом конкретном интервале, хотя это дает около 29 бит точности вместо 23 бит, которые вы просили. Если вы хотите выбрать другой интервал сокращения диапазона, есть несколько вариантов, которые могут сохранить термин, возможно, за несколько бит, которые вам не нужны.

log2(max(abs(sin(x) -sine(xt))))
ans =
      -29.182