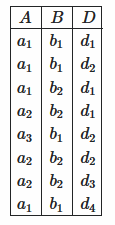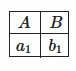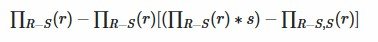Как понять `u=r÷s`, оператор деления, в реляционной алгебре?
let - база данных, имеющая следующие реляционные схемы: R(A,B,D) а также S(A,B) с атрибутами того же имени в том же домене и с экземплярами r а также n,
Экземпляр s
Какова схема и каковы кортежи u=r÷s? Как определить их на английском языке с r а также s?
Моя попытка
я знаю это
Это заставляет меня думать, что это будет только массив из одного столбца A, но я не уверен, что знаю, что будет в результате в массиве.
Можете ли вы помочь мне понять u=r÷s?
2 ответа
Интуитивное свойство оператора деления реляционной алгебры заключается просто в том, что оно является обратным к декартовому произведению. Например, если у вас есть два отношения R и S, то, если U является отношением, определенным как их декартово произведение:
U = R x S
деление является оператором таким, что:
U ÷ R = S
а также:
U ÷ S = R
Итак, вы можете думать о результате U ÷ R как: "проекция U что, умноженное на R, производит UИ операции ÷как операция, которая находит все "части" U которые объединяются со всеми кортежами R,
Однако, чтобы быть полезным, мы хотим, чтобы эта операция могла применяться к любой паре отношений, то есть мы хотим разделить отношение, которое не является результатом декартового произведения. Для этого формальное определение является более сложным.
Итак, предположим, что у нас есть два отношения R и S с атрибутами соответственно A и B, их деление можно определить как:
R ÷ S = πAB(R) - πAB((πAB(R) x S) - R)
это можно прочитать следующим образом:
πAB(R) x S: проецируйте R по атрибутам R, которых нет в S, и умножьте (декартово произведение) это отношение на S. Это дает отношение с атрибутами A к R и со строками все возможные комбинации ряды S и проекция R;
Из предыдущего результата вычтите все кортежи первоначально в R, то есть выполните (πAB(R) x S) - R. Таким образом, мы получаем "дополнительные" кортежи, то есть кортежи в декартовом произведении, которые не были присутствует в исходном отношении.
Наконец, вычтите из исходного отношения эти дополнительные кортежи (но, опять же, выполняйте эту операцию только с атрибутами R, которых нет в S). Итак, последняя операция: πAB(R) - πAB(результат шага 2).
Итак, подойдя к вашему примеру, проекция r на D равно:
(D)
d1
d2
d3
d4
и декартово произведение с s является:
(A, B, D)
a1 b1 d1
a1 b1 d2
a1 b1 d3
a1 b1 d4
Теперь мы можем удалить из этого набора кортежи, которые также были в исходном отношении rт.е. первые два кортежа и последний, так что мы получаем следующий результат:
(A, B, D)
a1 b1 d3
И, наконец, мы можем удалить предыдущие кортежи (спроецированные на D) из исходного отношения (снова спроецированные на D), то есть мы удалим:
(D)
d3
от:
(D)
d1
d2
d3
d4
и мы получаем следующий результат, который является окончательным результатом деления:
(D)
d1
d2
d4
Наконец, мы могли бы дважды проверить результат, умножив его на исходное соотношение s (который состоит только из кортежа (a1, b1)):
(A B D)
a1 b1 d1
a1 b1 d2
a1 b1 d4
И, глядя на строки исходного отношения rВы можете увидеть этот факт, который должен дать вам важное представление о значении оператора деления:
единственные значения столбца
Dвrкоторые присутствуют вместе с(a1, b1)(единственный кортежs), являютсяd1,d2а такжеd4,
Вы также можете увидеть другой пример в Википедии, и для подробного объяснения деления, вместе с его преобразованием SQL, вы можете посмотреть на эти слайды.
Дивизион (÷)
Отношение, возвращаемое оператором деления, возвращает те кортежи из отношения A, которые связаны с каждым кортежем B.
Чтобы операция деления была допустимой, атрибуты B являются правильным подмножеством атрибутов A.
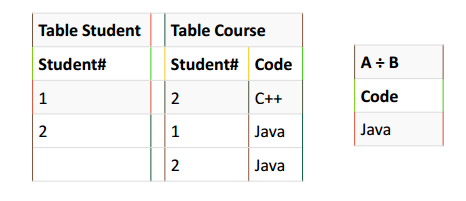
Table Course ÷ Table Student
Attributes in resulting relation = {Student#, Code} - {Student#} = Code
> Tuples in resulting relation = {Code} associated with all Student#’s
> tuple {1, 2}.