Может кто-нибудь объяснить, как отобразить эту сумму в MATLAB с помощью contourf?

Question

Я начну с того, что, да, это домашнее задание (мой первый домашний вопрос по stackru!). Но я не хочу, чтобы вы решили это за меня, я просто хочу получить руководство!

Уравнение в вопросе это: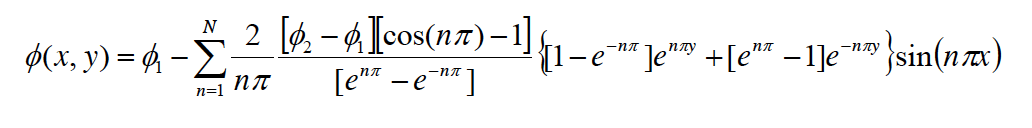

Мне говорят, что нужно взять N = 50, phi1 = 300, phi2 = 400, 0<=x<=1 и 0<=y<=1, и позволить x и y быть векторами из 100 одинаково расположенных точек, включая конечные точки.

Поэтому первое, что я сделал, - установил эти переменные и использовал x = linspace(0,1) и y = linspace(0,1) для создания правильных векторов.

Вопрос заключается в том, чтобы написать файл сценария MATLAB под названием потенциал.m, который вычисляет phi(x,y) и создает заполненный контурный график по сравнению с x и y, используя встроенную функцию contourf (см. Примеры в справочной команде в MATLAB). Убедитесь, что фигура помечена правильно. (Совет: верхняя и нижняя части вашего домена должны быть горячее примерно на 400 градусов по сравнению с левой и правой сторонами, которые должны быть под 300 градусов).

Однако ранее я вычислял фи, используя x или y в качестве константы. Как я должен рассчитать это, где оба являются переменными? Удерживаю ли я x при прохождении каждого числа в векторе y, присваивая его матрице, увеличивая x до следующего числа в его векторе после повторного прохождения каждого значения y снова и снова? И затем делать тот же процесс, но медленно увеличивая y вместо?

Если это так, я использовал цикл, который увеличивается до следующей строки каждый раз, когда проходит по всем 100 значениям. Если бы я сделал это таким образом, я бы получил массивную матрицу, состоящую из 200 строк и 100 столбцов. Как бы я использовал это в функции linspace?

Если это правильно, вот как я нахожу свою матрицу:

clear
clc
format compact
x = linspace(0,1);
y = linspace(0,1);
N = 50;
phi1 = 300;
phi2 = 400;
phi = 0;
sum = 0;
for j = 1:100
    for i = 1:100
        for n = 1:N
            sum = sum + ((2/(n*pi))*(((phi2-phi1)*(cos(n*pi)-1))/((exp(n*pi))-(exp(-n*pi))))*((1-(exp(-n*pi)))*(exp(n*pi*y(i)))+((exp(n*pi))-1)*(exp(-n*pi*y(i))))*sin(n*pi*x(j)));
        end
        phi(j,i) = phi1 - sum;
    end
end
for j = 1:100
    for i = 1:100
        for n = 1:N
            sum = sum + ((2/(n*pi))*(((phi2-phi1)*(cos(n*pi)-1))/((exp(n*pi))-(exp(-n*pi))))*((1-(exp(-n*pi)))*(exp(n*pi*y(j)))+((exp(n*pi))-1)*(exp(-n*pi*y(j))))*sin(n*pi*x(i)));
        end
        phi(j+100,i) = phi1 - sum;
    end
end

Это определение контура. Я думаю, что я должен использовать контур (X, Y, Z):

contourf(X, Y, Z), contourf(X, Y, Z, n) и contourf(X,Y,Z,v) рисуют заполненные контурные графики Z, используя X и Y для определения осей x и y пределы. Когда X и Y являются матрицами, они должны иметь тот же размер, что и Z, и должны монотонно увеличиваться.

Вот новый код:

N = 50;
phi1 = 300;
phi2 = 400;
[x, y, n] = meshgrid(linspace(0,1),linspace(0,1),1:N)
f = phi1-((2./(n.*pi)).*(((phi2-phi1).*(cos(n.*pi)-1))./((exp(n.*pi))-(exp(-n.*pi)))).*((1-(exp(-1.*n.*pi))).*(exp(n.*pi.*y))+((exp(n.*pi))-1).*(exp(-1.*n.*pi.*y))).*sin(n.*pi.*x));
g = sum(f,3);
[x1,y1] = meshgrid(linspace(0,1),linspace(0,1));
contourf(x1,y1,g)

Answer 1

Векторизация кода. Например, вы можете написать f(x,y,n) с:

 [x y n] = meshgrid(-1:0.1:1,-1:0.1:1,1:10);
 f=exp(x.^2-y.^2).*n ;

f 3D-матрица теперь просто sum над правильным измерением...

 g=sum(f,3);

для того, чтобы использовать contourfмы возьмем только 2D часть x,y:

 [x1 y1] = meshgrid(-1:0.1:1,-1:0.1:1);    
 contourf(x1,y1,g)

Answer 2

Причина, по которой ваш код так долго вычисляет phi Матрица в том, что вы предварительно не выделяли массив. Ошибка о размере происходит потому, что phi не 100х100. Но вместо того, чтобы исправить эти вещи, есть еще лучший способ...

MATLAB - это матричная лаборатория MATrix, поэтому этот тип уравнения довольно легко вычислить с помощью матричных операций. подсказки:

1. Вместо зацикливания значений, строк или столбцов x а также y построить матрицы для представления всех возможных входных комбинаций. Проверьте сетку для этого.

2. Вам все еще понадобится цикл для суммирования по n = 1:N. Но для каждого значения n вы можете оценить свое уравнение для всех x и y одновременно (используя матрицы из подсказки 1). Ключом к выполнению этой работы является использование поэлементных операторов, таких как .* а также ./,

Использование таких матричных операций - это The Matlab Way. Выучи это и люби это. (И расстраивайтесь, когда используете большинство других языков, у которых их нет.)

Удачи с домашней работой!