Свертка для цифровой обработки сигналов в R

Question

У меня есть простая цифровая система, которая имеет вход x(n) = u(n) - u(n-4).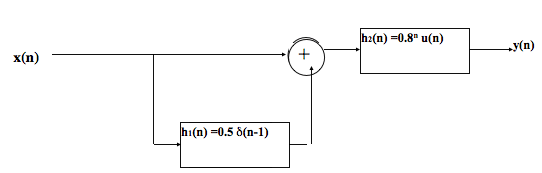

Я пытаюсь найти выходные данные y (n) с функцией conv () из пакета 'signal' или функцией convolve () из пакета 'stats' и построить график зависимости y (n) от n для -10 ≤ n ≤ 10.

Пока у меня есть следующий код:

library(signal)

n <- c(-10:10)                           # Time index
x <- c(rep(0, 10), rep(1, 4), rep(0, 7)) # Input Signal
h1 <- c(rep(0, 11), 0.5, rep(0, 9))      # Filter 1
h2 <- 0.8^n                              # Filter 2
h2[0:11] <- 0                            #

system <- data.frame(n, x, h1, h2)


y <- conv(x + conv(x, h1), h2)           # Output Signal

system <- transform(system, y=y[1:21]) 

plot(system$n, system$y)  

Я проверил этот сюжет, и это очень неправильно. Я думаю, что есть некоторая переработка векторов, когда я делаю свертку, и выходные данные функции conv (), похоже, не совпадают с исходным индексом времени. Я просто не могу понять, как исправить мою логику здесь. Я понимаю, что функция conv (n, m) возвращает вектор длины (m+n)-1, есть ли хороший способ легко сопоставить этот вектор с вектором временного индекса?

Это потребовало бы некоторых знаний о цифровой обработке сигналов, а также о кодировании на R, и было бы здорово, если бы кто-то имел опыт использования R для этой цели и мог бы дать несколько советов. Заранее спасибо.

Answer 1

Я понял это... Центр вывода функции conv() совпадает с центром вектора индекса времени. В качестве таких:

library(signal)

n <- c(-10:10)                           # Time index
x <- c(rep(0, 10), rep(1, 4), rep(0, 7)) # Input Signal, square pulse
h1 <- c(rep(0, 11), 0.5, rep(0, 9))      # Filter 1
h2 <- 0.8^n                              # Filter 2
h2[1:10] <- 0                            #

system <- data.frame(n, x, h1, h2)

y <- conv(x + conv(x, h1)[11:31], h2)    # Output Signal

system <- transform(system, y=y[11:31]) 

plot(system$n, system$y)

Я буду работать над общей формой, чтобы выполнить это, поскольку я буду делать это регулярно и не хотел бы делать это каждый раз вручную. Если кто-то победит меня, пожалуйста, поделитесь.:)

ОБНОВИТЬ

Создан общий вид функции conv() для автоматического выравнивания индексов входных и выходных векторов. Это происходит за счет того, что вы не получите полную свертку, поэтому вам придется настроить свой вход так, чтобы он сначала отображал всю интересующую вас область.

library(signal) # Should this be inside the func. with attach(), detach()?

conv2 <- function(x, y){
    conv(x, y)[ceiling(length(x)/2):(length(x)+floor(length(x)/2))]
}

# so 
y <- conv2(x + conv2(x, h1), h2)

ОБНОВЛЕНИЕ 2

Я хотел сравнить функцию с FFT. Я не совсем доволен этой версией, я хотел использовать sapply(), но она работает. На данный момент, это будет делать.. Я буду работать над улучшениями.

conv3 <- function(x, h){
m <- length(x)
n <- length(h)
X <- c(x, rep(floor(n/2), 0, floor(n/2)))   
H <- c(h, rep(floor(m/2), 0, floor(m/2)))
   Y <- vector()

for(i in 1:n+m-1){
    Y[i] <- 0 
    for(j in 1:m){
        Y[i] <- ifelse(i-j+1>0, Y[i] + X[j]*H[i-j+1], 0)
    }
}
Y[is.na(Y)] <- 0
Y[ceiling(m/2):(m+floor(m/2))]
}

Далее, я думаю, мне нужно работать над тем, чтобы сделать его многомерным.