Big-O для восьмилетних?

Question

Я спрашиваю больше о том, что это значит для моего кода. Я понимаю концепции математически, мне просто трудно понять, что они означают концептуально. Например, если кто-то должен выполнить операцию O(1) над структурой данных, я понимаю, что количество операций, которые он должен выполнить, не будет расти, потому что есть больше элементов. А операция O(n) будет означать, что вы будете выполнять набор операций для каждого элемента. Может ли кто-нибудь заполнить здесь пробелы?

• Например, что именно будет делать операция O(n^2)?
• И что, черт возьми, это значит, если операция O(n log(n))?
• И кто-то должен курить крэк, чтобы написать O(x!)?

Answer 1

Один из способов думать об этом:

O (N ^ 2) означает, что для каждого элемента вы делаете что-то с каждым другим элементом, например сравниваете их. Bubble sort является примером этого.

O (N log N) означает, что для каждого элемента вы делаете то, что нужно только для просмотра журнала N элементов. Обычно это происходит потому, что вы знаете что-то об элементах, что позволяет вам сделать эффективный выбор. Наиболее эффективными видами сортировки являются такие примеры, как сортировка слиянием.

O (N!) Означает что-то сделать для всех возможных перестановок N элементов. Путешествующий продавец - пример этого, где есть N! способы посещения узлов, и решение для грубой силы состоит в том, чтобы посмотреть на общую стоимость каждой возможной перестановки, чтобы найти оптимальную.

Answer 2

Самое важное, что обозначение Big-O означает для вашего кода, - это то, как он будет масштабироваться, когда вы удваиваете количество "вещей", над которыми он работает. Вот конкретный пример:

Биг-О | вычисления для 10 вещей | расчеты на 100 вещей
----------------------------------------------------------------------
O(1)        |   1                         |     1
O(log(n))   |   3                         |     7
O(n)        |  10                         |   100
O(n log(n)) |  30                         |   700
O(n^2)      | 100                         | 10000

Итак, возьмите быструю сортировку, которая является O (n log (n)), против пузырьковой сортировки, которая является O(n^2). При сортировке 10 вещей быстрая сортировка в 3 раза быстрее, чем при пузырьковой сортировке. Но при сортировке 100 вещей это в 14 раз быстрее! Очевидно, что выбор самого быстрого алгоритма очень важен. Когда вы попадаете в базы данных с миллионами строк, это может означать разницу между вашим запросом, выполняемым за 0,2 секунды, по сравнению с часами.

Еще одна вещь, которую следует учитывать, это то, что плохой алгоритм - это то, что закон Мура не может помочь. Например, если у вас есть какой-то научный расчет, который равен O(n^3), и он может вычислять 100 вещей в день, удвоение скорости процессора дает вам только 125 вещей в день. Тем не менее, доведите этот расчет до O (n ^ 2), и вы будете делать 1000 вещей в день.

пояснение: На самом деле, Big-O ничего не говорит о сравнительной производительности разных алгоритмов в одной и той же точке размера, а о сравнительной производительности одного и того же алгоритма в разных точках размера:

                 Вычисления Вычисления Вычисления Big-O       | на 10 вещей | на 100 вещей | на 1000 вещей ----------------------------------------------------------------------
O(1)        |        1        |        1        |         1
O(log(n))   |        1        |        3        |         7
O(n)        |        1        |       10        |       100
O(n log(n)) |        1        |       33        |       664
O(n^2)      |        1        |      100        |     10000

Answer 3

Вы можете найти это полезным для визуализации:

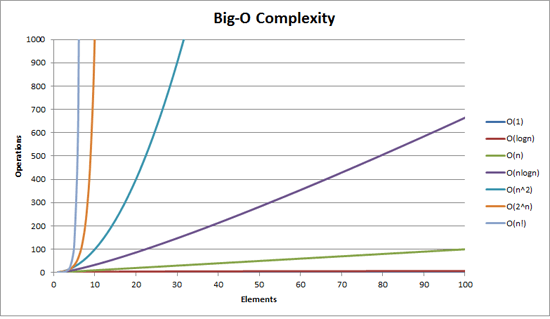
Кроме того, в масштабе LogY/LogX все функции n^1/2, n, n² выглядят как прямые линии, в то время как в масштабе LogY/X 2ⁿ, eⁿ, 10ⁿ - это прямые линии и n! является линейным (выглядит как n log n).

Answer 4

Это может быть слишком математично, но вот моя попытка. (Я математик.)

Если что-то есть O (f (n)), то время его работы на n элементах будет равно A f (n) + B (измеряется, скажем, в тактах или операциях ЦП). Это ключ к пониманию того, что у вас также есть эти константы A и B, которые возникают из конкретной реализации. B представляет собой "постоянные издержки" вашей операции, например, некоторую предварительную обработку, которую вы выполняете, которая не зависит от размера коллекции. A представляет скорость вашего фактического алгоритма обработки предметов.

Ключ, однако, в том, что вы используете большие обозначения O, чтобы выяснить, насколько хорошо что-то будет масштабироваться. Таким образом, эти константы не будут иметь большого значения: если вы пытаетесь выяснить, как масштабировать от 10 до 10000 элементов, кого волнуют постоянные накладные расходы B? Точно так же другие проблемы (см. Ниже), безусловно, перевесят вес мультипликативной константы A.

Таким образом, реальная сделка - это f (n). Если f растет совсем не при n, например, f (n) = 1, то вы будете фантастически масштабироваться - ваше время работы всегда будет просто A + B. Если f растет линейно с n, то есть f (n) = n, ваше время выполнения будет масштабироваться настолько хорошо, насколько можно ожидать - если ваши пользователи ждут 10 нс для 10 элементов, они будут ждать 10000 нс для 10000 элементы (без учета аддитивной постоянной). Но если он растет быстрее, как n ², то у вас проблемы; вещи начнут замедляться слишком сильно, когда вы получите большие коллекции. f (n) = n log (n) - это хороший компромисс, обычно: ваша операция не может быть настолько простой, чтобы обеспечить линейное масштабирование, но вам удалось сократить все так, что она будет масштабироваться намного лучше, чем f (n) = n ².

Практически, вот несколько хороших примеров:

• O (1): получение элемента из массива. Мы точно знаем, где это находится в памяти, поэтому мы просто идем за этим. Неважно, если в коллекции 10 предметов или 10000; он все еще находится в индексе (скажем) 3, поэтому мы просто переходим к месту 3 в памяти.
• O (n): получение элемента из связанного списка. Здесь, A = 0,5, потому что в среднем вам придется пройти 1/2 связанного списка, прежде чем вы найдете нужный элемент.
• O (n ²): различные "глупые" алгоритмы сортировки. Поскольку, как правило, их стратегия включает в себя, для каждого элемента (n), вы смотрите на все другие элементы (например, на другой n, давая n ²), затем позиционируете себя в правильном месте.
• O (n log (n)): различные "умные" алгоритмы сортировки. Оказывается, вам нужно только взглянуть, скажем, на 10 элементов в коллекции из 10-ти элементов, чтобы разумно отсортировать себя по отношению ко всем остальным в коллекции. Потому что все остальные также будут смотреть на 10 элементов, а возникающее поведение организовано точно так, чтобы этого было достаточно для создания отсортированного списка.
• O (n!): Алгоритм, который "пробует все", поскольку существует (пропорционально) n! возможные комбинации из n элементов, которые могут решить данную проблему. Таким образом, он просто просматривает все такие комбинации, пробует их, а затем останавливается всякий раз, когда это удается.

Answer 5

Ответ don.neufeld очень хороший, но я, вероятно, объясню его в двух частях: во-первых, существует грубая иерархия O(), в которую попадает большинство алгоритмов. Затем вы можете взглянуть на каждый из них, чтобы придумать эскизы того, что делают типичные алгоритмы того времени.

Для практических целей единственные O(), которые когда-либо имеют значение:

• O (1) "постоянное время" - требуемое время не зависит от размера входа. В качестве грубой категории я бы включил здесь такие алгоритмы, как поиск по хэшам и Union-Find, хотя ни один из них на самом деле не является O (1).
• O (log (n)) "логарифмический" - он становится медленнее по мере того, как вы получаете большие входные данные, но как только ваш входной сигнал становится достаточно большим, он не изменится настолько, чтобы о нем беспокоиться. Если ваша среда выполнения подходит для данных разумного размера, вы можете заполнить их дополнительным количеством данных, и вы все равно будете в порядке.
• O (n) "линейный" - чем больше входных данных, тем больше времени требуется для равномерного компромисса. В три раза размер ввода займет примерно в три раза больше времени.
• O(n log(n)) "лучше, чем квадратичный" - увеличение размера входных данных причиняет боль, но все еще управляемо. Алгоритм, вероятно, приличный, просто основная проблема сложнее (решения менее локализованы относительно входных данных), чем те проблемы, которые могут быть решены за линейное время. Если ваши входные размеры увеличиваются, не думайте, что вы могли бы обрабатывать вдвое больше размера, не меняя при этом свою архитектуру (например, перемещая вещи в пакетные вычисления за одну ночь, или не делая вещи за кадр). Это нормально, если размер ввода немного увеличивается; просто следите за множеством.
• O(n^2) "квадратичный" - он действительно будет работать только до определенного размера вашего ввода, поэтому обратите внимание на то, насколько большим он может стать. Кроме того, ваш алгоритм может быть отстойным - подумайте, чтобы увидеть, есть ли алгоритм O(n log(n)), который даст вам то, что вам нужно. Оказавшись здесь, вы будете очень благодарны за удивительное оборудование, которым мы были одарены. Не так давно то, что вы пытаетесь сделать, было бы невозможно для всех практических целей.
• O (n ^ 3) "кубический" - не качественно все, что отличается от O(n^2). Те же комментарии применимы, только больше. Есть хороший шанс, что более умный алгоритм может сократить это время до чего-то меньшего, например O(n^2 log(n)) или O(n^2.8...), но опять же, есть хороший шанс, что он не будет стоить хлопот (Вы уже ограничены в своем практическом размере ввода, поэтому постоянные факторы, которые могут потребоваться для более умных алгоритмов, вероятно, уменьшат их преимущества для практических случаев. Кроме того, медленное мышление; позволить компьютеру пережевать это может сэкономить ваше время в общем и целом.)
• O (2 ^ n) "экспоненциальный" - проблема либо принципиально сложна в вычислительном отношении, либо вы идиот. Эти проблемы имеют узнаваемый вкус. Ваши входные размеры ограничены довольно жестким ограничением. Вы быстро узнаете, соответствуете ли вы этому пределу.

И это все. Есть много других возможностей, которые подходят между ними (или больше, чем O(2^n)), но они не часто случаются на практике, и они качественно не сильно отличаются от одного из них. Кубические алгоритмы уже немного растянуты; Я включил их только потому, что сталкивался с ними достаточно часто, чтобы о них стоило упомянуть (например, умножение матриц).

Что на самом деле происходит с этими классами алгоритмов? Ну, я думаю, что вы хорошо начали, хотя есть много примеров, которые не соответствуют этим характеристикам. Но для вышесказанного я бы сказал, что обычно это выглядит примерно так:

• O (1) - вы смотрите только на фиксированный размер ваших входных данных, и, возможно, ни на один из них. Пример: максимум отсортированного списка.
  • Или ваш входной размер ограничен. Пример: сложение двух чисел. (Обратите внимание, что добавление N чисел является линейным временем.)
• O (log n) - каждый элемент вашего ввода говорит вам достаточно, чтобы игнорировать большую часть остального ввода. Пример: когда вы смотрите на элемент массива в бинарном поиске, его значение говорит вам, что вы можете игнорировать "половину" вашего массива, не глядя ни на что из этого. Или аналогичным образом, элемент, на который вы смотрите, дает вам достаточно сводной информации о доле оставшихся входных данных, поэтому вам не нужно будет на них смотреть.
  • Хотя в половинках нет ничего особенного - если вы можете игнорировать только 10% своего ввода на каждом шаге, это все равно логарифмический.
• O (n) - вы выполняете фиксированный объем работы для каждого элемента ввода. (Но смотри ниже.)
• O(n log(n)) - есть несколько вариантов.
  • Вы можете разделить входные данные на две группы (не более чем за линейное время), решить проблему независимо для каждой группы, а затем объединить две группы, чтобы сформировать окончательное решение. Независимость двух свай имеет ключевое значение. Пример: классический рекурсивный слияние.
  • Каждый линейный проход данных приводит вас на полпути к вашему решению. Пример: быстрая сортировка, если вы думаете с точки зрения максимального расстояния каждого элемента до его окончательной отсортированной позиции на каждом шаге разбиения (и да, я знаю, что на самом деле это O(n^2) из-за вырожденных опорных вариантов. Но на практике это попадает в мою категорию O(n log(n)).)
• O(n^2) - вы должны смотреть на каждую пару входных элементов.
  • Или нет, но вы думаете, что вы делаете, и вы используете неправильный алгоритм.
• O (n ^ 3) - хм... у меня нет резкой характеристики этого. Это, вероятно, один из:
  • Вы умножаете матрицы
  • Вы просматриваете каждую пару входов, но операция, которую вы делаете, требует повторного просмотра всех входов
  • вся структура графика вашего ввода актуальна
• O(2^n) - вам нужно рассмотреть все возможные подмножества ваших входов.

Ничто из этого не является строгим. Особенно не линейные алгоритмы времени (O(n)): я мог бы привести несколько примеров, где вы должны посмотреть на все входные данные, затем на половину, затем на половину и т. Д. Или наоборот -- вы складываете пары входов, затем рекурсируете на выходе. Они не соответствуют описанию выше, так как вы не смотрите на каждый вход по одному разу, но он все равно появляется в линейном времени. Тем не менее, в 99,2% случаев линейное время означает просмотр каждого входа один раз.

Answer 6

Я пытаюсь объяснить, давая простые примеры кода на C#.

За List<int> numbers = new List<int> {1,2,3,4,5,6,7,12,543,7};

O(1) выглядит как

return numbers.First();

O(n) выглядит как

int result = 0;
foreach (int num in numbers)
{
    result += num;
}
return result;

O(n log(n)) выглядит так

int result = 0;
foreach (int num in numbers)
{
    int index = numbers.length - 1;
    while (index > 1)
    {
        // yeah, stupid, but couldn't come up with something more useful :-(
        result += numbers[index];
        index /= 2;
    }
}
return result;

O(n^2) выглядит так

int result = 0;
foreach (int outerNum in numbers)
{
    foreach (int innerNum in numbers)
    {
        result += outerNum * innerNum;
    }
}
return result;

O(n!) Похоже на усталость придумывать что-нибудь простое.
Но я надеюсь, что вы поняли основную мысль?

Answer 7

Многие из них легко продемонстрировать с помощью чего-то непрограммирующего, например, тасования карт.

Сортировка колоды карт, пройдя всю колоду, чтобы найти туз пик, затем пройдя всю колоду, чтобы найти 2 пик, и так далее, будет наихудшим случаем n^2, если колода уже отсортирована в обратном направлении. Вы посмотрели все 52 карты 52 раза.

В общем, действительно плохие алгоритмы не обязательно являются преднамеренными, они обычно злоупотребляют чем-то другим, например, вызывают метод, который является линейным внутри некоторого другого метода, который повторяется над тем же набором линейно.

Answer 8

Хорошо, здесь есть несколько очень хороших ответов, но почти все они, кажется, делают одну и ту же ошибку, и это распространенная практика.

Неофициально мы пишем, что f(n) = O( g(n)), если с точностью до коэффициента масштабирования и для всех n, больших некоторого n0, g(n) больше, чем f (n). То есть f (n) растет не быстрее, чем g (n), или ограничено сверху. Это ничего не говорит нам о том, как быстро растет f (n), за исключением того факта, что он гарантированно не будет хуже, чем g (n).

Конкретный пример: n = O( 2^n). Все мы знаем, что n растет гораздо реже, чем 2^n, что дает нам право говорить, что оно ограничено сверху экспоненциальной функцией. Между n и 2 ^ n есть много места, так что это не очень жесткая граница, но это все же законная граница.

Почему мы (компьютерные ученые) используем границы, а не точные? Потому что а) границы часто легче доказать и б) это дает нам возможность выразить свойства алгоритмов. Если я скажу, что мой новый алгоритм O(n.log n), это означает, что в худшем случае его время выполнения будет ограничено сверху n.log n на n входах, для достаточно больших n (хотя см. Мои комментарии ниже когда я не имею в виду худший случай).

Если вместо этого мы хотим сказать, что функция растет точно так же быстро, как и некоторые другие функции, мы используем тета, чтобы подчеркнуть эту точку (я напишу T( f(n)), чтобы обозначить \Theta из f (n) в уценке), T( g(n)) - это сокращение от ограничения сверху и снизу g (n), опять же, до коэффициента масштабирования и асимптотически.

То есть f(n) = T( g(n)) <=> f(n) = O(g(n)) и g(n) = O(f(n)). В нашем примере мы можем видеть, что n!= T( 2^n), потому что 2^n!= O(n).

Зачем беспокоиться об этом? Потому что в своем вопросе вы пишете: "Кому-то придется курить, чтобы написать O(x!)?" Ответ - нет, потому что в основном все, что вы пишете, будет ограничено сверху факториальной функцией. Время выполнения быстрой сортировки - O (n!) - это не жесткая граница.

Здесь также есть другое измерение тонкости. Обычно речь идет о вводе в худшем случае, когда мы используем нотацию O (g (n)), поэтому мы делаем составное утверждение: в худшем случае время выполнения не будет хуже алгоритма, который принимает g (n).) шаги, опять же по модулю масштабирования и для достаточно большого n. Но иногда мы хотим поговорить о времени выполнения среднего и даже лучших случаях.

Ванильная быстрая сортировка, как всегда, хороший пример. Это T( n^2) в худшем случае (на самом деле потребуется не менее n ^ 2 шагов, но не намного больше), но T(n.log n) в среднем случае, то есть ожидаемое число шаги пропорциональны n.log n. В лучшем случае это также T(n.log n), но вы могли бы улучшить это, например, для проверки, был ли массив уже отсортирован, и в этом случае наилучшим временем выполнения будет T( n).

Как это связано с вашим вопросом о практической реализации этих границ? Ну, к сожалению, запись O() скрывает константы, с которыми приходится иметь дело в реальных реализациях. Поэтому, хотя мы можем сказать, что, например, для операции T( n^2) мы должны посетить каждую возможную пару элементов, но мы не знаем, сколько раз нам нужно их посещать (за исключением того, что это не функция п). Таким образом, мы могли бы посещать каждую пару 10 раз или 10^10 раз, и оператор T( n^2) не делает различий. Функции более низкого порядка также скрыты - мы могли бы посетить каждую пару элементов один раз и каждый отдельный элемент 100 раз, потому что n^2 + 100n = T(n^2). Идея записи O() заключается в том, что для достаточно большого n это вообще не имеет значения, потому что n ^ 2 становится намного больше, чем 100n, что мы даже не замечаем влияния 100n на время выполнения. Тем не менее, мы часто имеем дело с "достаточно маленькими" n, такими, что постоянные факторы и т. Д. Имеют реальное, существенное значение.

Например, быстрая сортировка (средняя стоимость T(n.log n)) и heapsort (средняя стоимость T(n.log n)) являются алгоритмами сортировки с одинаковыми средними затратами, однако быстрая сортировка обычно намного быстрее, чем heapsort. Это связано с тем, что heapsort выполняет на несколько элементов больше сравнений, чем quicksort.

Это не означает, что запись O() бесполезна, просто неточна. Это довольно тупой инструмент для малого n.

(В качестве последнего примечания к этому трактату, помните, что нотация O() просто описывает рост любой функции - это не обязательно должно быть время, это может быть память, сообщения, которыми обмениваются в распределенной системе, или количество процессоров, необходимых для параллельный алгоритм.)

Answer 9

То, как я описываю это своим нетехническим друзьям, выглядит так:

Рассмотрим многозначное сложение. Хорошее старомодное, карандашное и бумажное дополнение. То, что вы узнали, когда вам было 7-8 лет. Имея два числа из трех или четырех цифр, вы можете довольно легко выяснить, к чему они складываются.

Если бы я дал вам два 100-значных числа и спросил, к чему они сводятся, выяснить это было бы довольно просто, даже если бы вам пришлось использовать карандаш и бумагу. Яркий ребенок может сделать такое дополнение всего за несколько минут. Это потребует только около 100 операций.

Теперь рассмотрим многозначное умножение. Вы, наверное, узнали это в возрасте 8 или 9 лет. Вы (надеюсь) сделали много повторяющихся упражнений, чтобы изучить механику, стоящую за этим.

Теперь представьте, что я дал вам те же два 100-значных числа и сказал вам умножить их вместе. Это было бы гораздо более сложной задачей, что заняло бы у вас несколько часов, и что вы вряд ли обойдетесь без ошибок. Причина этого заключается в том, что (эта версия) умножения составляет O(n^2); каждая цифра в нижнем числе должна быть умножена на каждую цифру в верхнем числе, оставляя в общей сложности около n ^ 2 операций. В случае 100-значных чисел это 10 000 умножений.

Answer 10

Я думаю об этом: у вас есть задача устранить проблему, вызванную злым злодеем V, который выбирает N, и вы должны оценить, сколько еще потребуется времени, чтобы закончить вашу проблему, когда он увеличивает N.

O (1) -> увеличение N действительно не имеет никакого значения

O(log(N)) -> каждый раз, когда V удваивает N, вам нужно потратить дополнительное количество времени T, чтобы выполнить задачу. V снова удваивает N, и вы тратите столько же.

O (N) -> каждый раз, когда V удваивает N, вы тратите вдвое больше времени.

O (N ^ 2) -> каждый раз, когда V удваивает N, вы тратите в 4 раза больше времени. (это нечестно!!!)

O (N log (N)) -> каждый раз, когда V удваивает N, вы тратите вдвое больше времени и немного больше.

Это границы алгоритма; ученые-компьютерщики хотят описать, сколько времени потребуется для больших значений N. (что становится важным, когда вы учитываете числа, используемые в криптографии - если компьютеры ускоряются в 10 раз, сколько еще битов делают Вы должны использовать его, чтобы убедиться, что им потребуется 100 лет, чтобы взломать ваше шифрование, а не только 1 год?)

Некоторые из границ могут иметь странные выражения, если это имеет значение для вовлеченных людей. Я видел такие вещи, как O(N log(N) log(log(N))) где-то в "Искусстве компьютерного программирования" Кнута для некоторых алгоритмов. (не могу вспомнить, что с моей головы)

Answer 11

Нет, алгоритм O(n) не означает, что он будет выполнять операцию с каждым элементом. Нотация Big-O дает вам возможность говорить о "скорости" вашего алгоритма независимо от вашей реальной машины.

O(n) означает, что время, затрачиваемое вашим алгоритмом, растет линейно по мере увеличения вашего ввода. O(n^2) означает, что время, затрачиваемое вашим алгоритмом, увеличивается как квадрат вашего ввода. И так далее.

Answer 12

Одна вещь, которая еще не была затронута по какой-то причине:

Когда вы видите алгоритмы с такими вещами, как O(2^n) или O(n^3) или другими неприятными значениями, это часто означает, что вам придется принять несовершенный ответ на вашу проблему, чтобы получить приемлемую производительность.

Правильные решения, которые взрываются подобным образом, часто встречаются при решении задач оптимизации. Почти правильный ответ, доставленный в разумные сроки, лучше, чем правильный ответ, полученный после того, как машина заглохла.

Рассмотрим шахматы: я не знаю точно, каким считается правильное решение, но это, вероятно, что-то вроде O(n^50) или даже хуже. Теоретически невозможно, чтобы любой компьютер действительно вычислил правильный ответ - даже если вы используете каждую частицу во вселенной в качестве вычислительного элемента, выполняющего операцию в минимально возможное время для жизни вселенной, у вас все еще остается много нулей, (Может ли квантовый компьютер решить эту проблему - другой вопрос.)

Answer 13

• И кто-то должен курить крэк, чтобы написать O(x!)?

Нет, просто используйте Пролог. Если вы написали алгоритм сортировки в Прологе, просто описав, что каждый элемент должен быть больше, чем предыдущий, и позвольте обратному отслеживанию выполнить сортировку за вас, это будет O(x!). Также известен как "сортировка перестановок".

Answer 14

"Интуиция" за Big-O

Представьте себе "конкуренцию" между двумя функциями над x, когда x приближается к бесконечности: f(x) и g(x).

Теперь, если с некоторой точки (некоторый x) одна функция всегда имеет более высокое значение, чем другая, то давайте назовем эту функцию "быстрее", чем другую.

Так, например, если для каждого x > 100 вы видите, что f (x)> g(x), то f (x) "быстрее", чем g(x).

В этом случае мы бы сказали, что g(x) = O(f(x)). f(x) представляет собой своего рода "ограничение скорости" для g(x), так как в конечном итоге оно проходит его и оставляет его навсегда.

Это не совсем определение обозначения big-O, в котором также говорится, что f (x) должно быть больше, чем C*g(x) для некоторой константы C (что является еще одним способом сказать, что вы не можете помогите g (x) выиграть соревнование, умножив его на постоянный коэффициент - f(x) всегда победит в конце). Формальное определение также использует абсолютные значения. Но я надеюсь, что мне удалось сделать это интуитивно понятным.

Answer 15

Мне нравится ответ дона Нойфельда, но я думаю, что могу кое-что добавить о O(n log n).

Алгоритм, который использует простую стратегию "разделяй и властвуй", вероятно, будет O(log n). Простейший пример этого - найти что-то в отсортированном списке. Вы не начинаете с самого начала и не сканируете его. Вы идете в середину, вы решаете, следует ли вам идти назад или вперед, прыгаете на полпути к последнему месту, которое вы искали, и повторяете это, пока не найдете нужный предмет.

Если вы посмотрите на алгоритмы быстрой сортировки или сортировки слиянием, вы увидите, что они оба используют метод разделения списка, который будет отсортирован пополам, сортировки каждой половины (с использованием одного и того же алгоритма, рекурсивно), а затем рекомбинации двух половин. Этот вид рекурсивной стратегии "разделяй и властвуй" будет O(n log n).

Если вы тщательно обдумаете это, то увидите, что быстрая сортировка выполняет алгоритм разделения O(n) на целые n элементов, затем O(n) дважды на n/2, затем 4 раза на n/4, и т. д.... пока вы не доберетесь до n разделов по 1 элементу (который вырожден). Число раз, когда вы делите n пополам, чтобы получить 1, примерно равно log n, и каждый шаг равен O(n), поэтому рекурсивное деление и захват - O(n log n). Mergesort строит другой путь, начиная с n рекомбинаций из 1 элемента и заканчивая 1 рекомбинацией из n элементов, где рекомбинация двух отсортированных списков равна O(n).

Что касается курить крэк, чтобы написать алгоритм O(n!), То вы, если у вас нет выбора. Приведенная выше проблема коммивояжера считается одной из таких проблем.

Answer 16

Думайте об этом как о сложении блоков lego (n) вертикально и перепрыгивании через них.

O (1) означает, что на каждом этапе вы ничего не делаете. Высота остается неизменной.

O (n) означает, что на каждом шаге вы складываете блоки c, где c1 - константа.

O (n ^ 2) означает, что на каждом шаге вы складываете c2 x n блоков, где c2 - это константа, а n - количество сложенных блоков.

O (nlogn) означает, что на каждом шаге вы складываете c3 x n x log n блоков, где c3 - это константа, а n - количество сложенных блоков.

Answer 17

Большинство книг Джона Бентли (например, " Программирование жемчуга") действительно прагматично освещают подобные вещи. Этот разговор, который он дал, включает один такой анализ быстрой сортировки.

Хотя Кнут и не совсем относился к этому вопросу, у него возникла интересная идея: преподавать нотацию Big-O на уроках старшеклассного исчисления, хотя я нахожу эту идею довольно эксцентричной.

Answer 18

Чтобы оставаться искренним на заданный вопрос, я отвечал на вопрос так же, как на 8-летнего ребенка.

Предположим, продавец мороженого готовит несколько видов мороженого (скажем, N) разных форм, упорядоченных по порядку. Вы хотите съесть мороженое, лежащее посередине

Случай 1: - Мороженое можно есть, только если вы съели все мороженое меньше его. Вам придется съесть половину всего приготовленного мороженого (вход). Ответ напрямую зависит от размера входного сигнала. Решение будет порядка o(N)

Случай 2:- Вы можете прямо съесть мороженое в середине

Решение будет O(1)

Случай 3: Вы можете съесть мороженое, только если вы съели все мороженое меньше его, и каждый раз, когда вы едите мороженое, вы позволяете другому ребенку (каждый раз новый ребенок) съесть все его мороженое. + N + N.......(N/2) раза Решение будет O(N2)

Answer 19

Чтобы понять O(n log n), помните, что log n означает log-base-2 of n. Затем посмотрите на каждую часть:

O (n), более или менее, когда вы работаете с каждым элементом в наборе.

O (log n) - это когда число операций совпадает с показателем степени, на который вы возводите 2, чтобы получить количество элементов. Бинарный поиск, например, должен сократить набор в половину журнала n раз.

O (n log n) - это комбинация - вы делаете что-то вроде бинарного поиска для каждого элемента в наборе. Эффективные сортировки часто работают, выполняя один цикл на элемент, и в каждом цикле проводят хороший поиск, чтобы найти правильное место для размещения данного элемента или группы. Следовательно, n * log n.

Answer 20

Скажите, что ваш восьмилетний журнал (n) означает, сколько раз вам нужно нарезать длину n журнала на две части, чтобы она уменьшилась до размера n = 1: p

O (n log n) обычно сортирует O(n^2) обычно сравнивает все пары элементов

Answer 21

Просто чтобы ответить на пару комментариев на мой пост выше:

Доменик - я на этом сайте, и мне все равно. Не ради педантичности, а потому, что мы - программисты - обычно заботимся о точности. Неправильное использование записи O() в стиле, который некоторые здесь сделали, делает его вроде бессмысленным; с таким же успехом мы можем сказать, что что-то занимает n^2 единиц времени, как O( n^2) в соответствии с соглашениями, используемыми здесь. Использование O() ничего не добавляет. Я говорю не о небольшом несоответствии между обычным использованием и математической точностью, а о том, насколько оно значимо, а что нет.

Я знаю много, много отличных программистов, которые точно используют эти термины. Сказать: "О, мы программисты, поэтому нам все равно" удешевляет все предприятие.

onebyone - Ну, не совсем, хотя я понимаю вашу точку зрения. Это не O(1) для произвольно большого n, что является своего рода определением O(). Это просто говорит о том, что O() имеет ограниченную применимость для ограниченного n, где мы скорее поговорим о количестве сделанных шагов, чем о ограничении этого числа.

Answer 22

Помните басню о черепахе и зайце (черепахе и кролике)?

В долгосрочной перспективе победит черепаха, но в краткосрочной перспективе победит заяц.

Это как O (logN) (черепаха) против O (N) (заяц).

Если два метода отличаются по своему большому O, то существует уровень N, на котором один из них победит, но Big O ничего не говорит о том, насколько велико это N.

Answer 23

Предположим, у вас есть компьютер, который может решить проблему определенного размера. Теперь представьте, что мы можем удвоить производительность в несколько раз. Насколько большую проблему мы можем решить с каждым удвоением?

Если мы сможем решить проблему двойного размера, это O(n).

Если у нас есть некоторый множитель, который не один, это своего рода полиномиальная сложность. Например, если каждое удвоение позволяет нам увеличить размер задачи примерно на 40%, это O(n^2), а около 30% будет O(n^3).

Если мы просто добавим к размеру проблемы, он будет экспоненциальным или хуже. Например, если каждое удвоение означает, что мы можем решить задачу на 1 больше, это O(2^n). (Вот почему грубое шифрование ключа становится практически невозможным с ключами разумного размера: 128-битный ключ требует примерно в 16 квинтиллионов раз больше обработки, чем 64-битный.)

Answer 24

Я постараюсь написать объяснение для настоящего восьмилетнего мальчика, кроме технических терминов и математических понятий.

Как то, что именно O(n^2) операцию делать?

Если вы в гостях, и есть n люди в партии, включая вас. Сколько нужно рукопожатий, чтобы все рукопожатие всех остальных, учитывая, что люди, вероятно, забудут, кто они рукопожатие в какой-то момент.

Примечание: это приближается к симплексу n(n-1) что достаточно близко к n^2,

И что, черт возьми, это значит, если операция O(n log(n))?

Ваша любимая команда победила, они стоят в очереди, и есть n игроки в команде. Сколько хэнсхэков понадобится вам для рукопожатия каждого игрока, учитывая, что вы будете хэнсхэкировать каждый по несколько раз, сколько раз, сколько цифр в числе игроков n,

Примечание: это даст n * log n to the base 10,

И кто-то должен курить крэк, чтобы написать O(x!)?

Вы богатый ребенок, и в вашем гардеробе много одежды, есть x ящики для каждого типа одежды, ящики рядом друг с другом, в первом ящике есть 1 предмет, в каждом ящике столько же тканей, сколько в ящике слева и еще один, так что у вас есть что-то вроде 1 шапка, 2 парики, .. (x-1) штаны, то x рубашки. Теперь, во сколько способов вы можете одеться, используя один предмет из каждого ящика.

Примечание: этот пример показывает, сколько листьев в дереве решений, где number of children = depthчто делается через 1 * 2 * 3 * .. * x

Answer 25

log(n) означает логарифмический рост. Примером могут служить алгоритмы "разделяй и властвуй". Если у вас есть 1000 отсортированных чисел в массиве (например, 3, 10, 34, 244, 1203 ...) и вы хотите найти число в списке (найти его позицию), вы можете начать с проверки значения число с индексом 500. Если оно ниже того, что вы ищете, перейдите к 750. Если оно выше, чем то, что вы ищете, перейдите к 250. Затем вы повторяете процесс, пока не найдете свое значение (и ключ). Каждый раз, когда мы прыгаем половину пространства поиска, мы можем отбросить тестирование многих других значений, поскольку мы знаем, что число 3004 не может быть выше числа 5000 (помните, это отсортированный список).

Тогда n log(n) означает n * log(n).