R - выборка пар для удовлетворения условия
У меня есть эта проблема, которую я не могу понять. У меня 500 образцов группы А из равномерного распределения. И есть 500 образцов группы B из другого равномерного распределения.
Я выберу одно значение, a из A, и другое значение, b из B. Я хочу, чтобы "a всегда было меньше, чем b". Я хотел бы получить 500 пар без дублирования.
A <- runif(500, min = 19, max= 23)
B <- runif(500, min = 22, max= 26)
Как я могу получить 500 пар (a,b), которые являются Спасибо! Извините, мне нужно прояснить мой вопрос. Как только группа A и B установлены, они не будут изменены. 500 пар должны быть выбраны из фиксированных A и B. В каждой паре a Я хочу видеть "случайный" эффект, как Монте-Карло. поэтому, я думаю, что только сортировка не может помочь этой проблеме. Спасибо!Отредактированный!!
6 ответов
Это тоже не самое красивое решение. Во всяком случае, я решил это! Я использовал пример функции с условием и заменил выбранное значение на NA, чтобы избежать дублирования.
A <- runif(500, min = 19, max= 23)
B <- runif(500, min = 22, max= 26)
B.largerthan.A <- function(A,B) {
result = c()
i <- 1
while (i < 500) {
Select.B <- sample(B[!is.na(B)], size=1)
if ( (Select.B < max(A,na.rm=TRUE)) & (!is.na(Select.B)) ) {
Select.A <- sample((A)[(A<Select.B) & (!is.na(A))], size=1)
} else {
Select.A <- sample((A[!is.na(A)]),size=1)
}
result = rbind(result, c(Select.A, Select.B))
A[which(A == Select.A)] = NA
B[which(B == Select.B)] = NA
i=1+i
if (length(B[!is.na(B)]) == 1) {
Select.B <- B[!is.na(B)]
Select.A <- A[!is.na(A)]
result = rbind(result, c(Select.A, Select.B))
A[which(A == Select.A)] = NA
B[which(B == Select.B)] = NA
break
}}
return(result)
}
A_B <- B.largerthan.A(A,B)
Это дает:
> any(A_B[,1] < A_B[,2])
[1] TRUE
Если у вас есть идея более аккуратная. Пожалуйста, дайте мне знать. БЛАГОДАРЮ ВАС!!
Сохранение моего предыдущего ответа ниже основано на моей первоначальной интерпретации вопроса.
Я не думаю, что поставленный вопрос представляет реальную проблему, которую вы пытаетесь решить. Я бы предложил опубликовать больше информации по основной проблеме, чтобы дать больше мотивации.
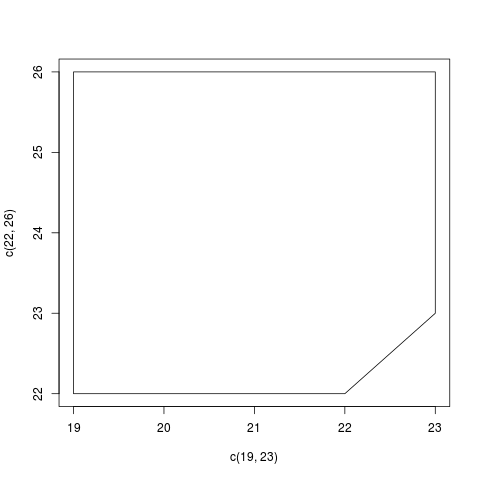
Чтобы суммировать постановку задачи как есть, вы хотите соединить A с перестановкой B это удовлетворяет условию, что A<B, Кроме того, вы хотите, чтобы результирующий набор пар был равномерно распределен по результирующему набору, который выглядит следующим образом:
Проблема в том, что значения х здесь равномерно распределены по [19,23]Это означает, что все полосы значений x будут иметь одинаковое количество точек, а поскольку правые полосы имеют меньший объем (из-за исключенного треугольника), плотность будет выше на этой стороне. Таким образом, невозможно добиться равномерной выборки с помощью любой перестановки B,
Если вы планируете использовать этот дистрибутив для оценки Монте-Карло чего-то внутри этого объекта, ваш результат будет неверным, потому что вы будете подвергаться избыточной выборке в некоторых частях набора и, следовательно, в других.
Единственный способ исправить это - либо повторно сэмплировать, как показано ниже, либо просто отбросить все пары, попадающие в этот угол, и использовать менее 500 точек для вычисления.
Я думаю, что это только частично программный вопрос.
Прежде всего, что вы подразумеваете под "дублированием"? runif Крайне маловероятно, чтобы получить дубликаты в смысле численно идентичных значений.
Предполагая, что мы можем игнорировать это условие, это вопрос выборки отклонения; а именно, вы хотите сделать выборку из прямоугольника с отсеченным углом. В частности, это квадрат 5х5 (область 25) минус треугольник 1х1 (область 1/2). Самый простой способ сделать это - взять большее количество, а затем взять первые 500, которые удовлетворяют условию.
Если мы начнем с фрейма данных размером 1000
df <- data.frame(A=runif(1000, min=19, max=23), B=runif(1000, min=22, max=26))
Мы можем отфильтровать и получить первые 500:
df2 <- head(df[df$A < df$B, ], 500)
rownames(df2) <- NULL
Поскольку диапазон A и B различен, мы можем отсортировать наборы и проверить, дают ли отсортированные векторы пары, которые удовлетворяют требуемому условию.
C <- sort(A)
D <- sort(B)
Теперь нам нужно проверить, есть ли пары C[i], D[i] выполнить условие C[i] < D[i] для всех i:
> !!sum(C > D)
#[1] FALSE
В этом случае нам повезло: все пары удовлетворяют необходимому условию. Если этот тест вернулся TRUEмы могли бы попытаться сгенерировать новые наборы случайных чисел.
Теперь у нас есть пары C[i], D[i] с записями, выбранными из A а также Bсоответственно такой, что C[i] < D[i] для всех 500 значений i,
Дублирование практически невозможно в числах с плавающей точкой.
Если необходимо извлечь из оригинальных A и B, я предлагаю это:
A <- runif(500, min = 19, max= 23)
B <- runif(500, min = 22, max= 26)
used <- rep(F, 500)
library("foreach")
newB <- foreach(a=A, .combine=c) %do% {
ind <- which(B>a & !used) # pool of available B values
if (length(ind)==0) # ie no remaining element of B is over a!
stop("This is quite unlikely but let's catch it just in case")
b <- B[ind] # pool of available B values
i <- sample(length(b), 1) # draw an index at random from b
### code was faulty here
used[ind[i]] <- T # flag it as used, it won't be drawn again
###
return(b[i]) # return the value
}
foreach(b=B, a=A, .export="B", .final=function(x) {print("Everything is ok")}) %do% {
if(sum(newB %in% b)>1)
stop("There are duplicates")
}
foreach(b=newB, a=A, .export="B", .final=function(x) {print("Everything is ok")}) %do% {
if(a>b)
stop("There are invalid pairs")
}
Который дает:
[1] "Все хорошо"
Здесь нет ни дубликатов, ни недопустимых пар.
РЕДАКТИРОВАТЬ: я исправил это. Очевидно, что тест, что все было в порядке, тоже был сломан, он также исправлен.
Посмотри, работает ли это.
Данные
A <- runif(500, min = 19, max= 23)
B <- runif(500, min = 22, max= 26)
Сеть Саппли И Лэппли
result<-sapply(B,function(b){b>lapply(A,function(a){a})})
Извлечение индексов
indices<-which(result,arr.ind = TRUE)
Использование индексов для подстановки векторов A и B и размещения всех пар в кадре данных
df<-as.data.frame(x=cbind(A=A[indices[,1]],B=B[indices[,2]]))
Взять 500 образцов из этого
library(dplyr)
df_sampled<-sample_n(df,500)
Некоторые тесты
all(df$A %in% A)
[1] TRUE
all(df$B %in% B)
[1] TRUE
all(df$A < df$B)
[1] TRUE
Это дает фрейм данных гораздо больших пар, чем 500. Мы можем легко взять 500 отсчетов из этого:)
Некоторые образцы из результирующего фрейма данных
sample_n(df,10)
A B
79298 19.95930 25.24061
8990 22.47500 25.00853
151784 19.50021 25.81786
189713 20.82555 25.68779
27653 21.47545 23.62572
180116 22.36681 22.50472
52052 21.00113 24.63401
171574 20.11955 22.89538
88720 19.22706 23.98680
25766 21.88181 24.56297
Не самое красивое решение, но оно работает. Тщательно выбирайте возможные минимальные и максимальные значения для A и B.
A <- runif(500, min = 19, max= 23)
B <- runif(500, min = 22, max= 26)
while(any(A>B)) {
i <- which(A>B)
A[i] <- runif(length(i), min = 19, max= 23)
}
Вот и ты.
> any(A>B)
[1] FALSE
Дублирование не является проблемой, поскольку вы рисуете из непрерывного распространения.
Ожидаемое количество итераций цикла оставлено в качестве упражнения для читателя.
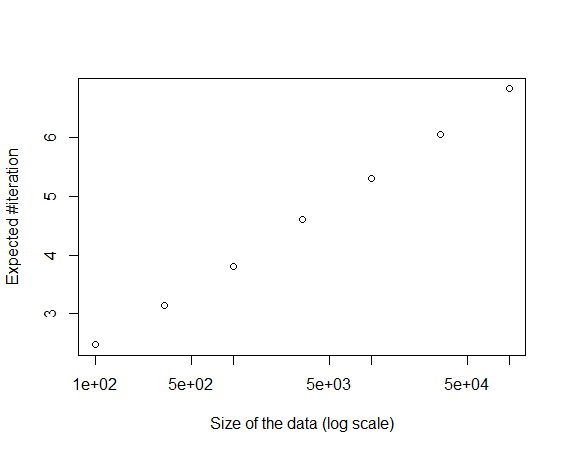
РЕДАКТИРОВАТЬ: ну, мне стало любопытно, вот как выглядит среднее число итераций, построенное по отношению к числу строк данных.
Как видите, это в O(log(size)),
Код:
library(foreach)
x <- 10^seq(2,5,.5)
res <- foreach(size=x, .combine=data.frame) %:%
times(1000) %do% {
A <- runif(size, min = 19, max= 23)
B <- runif(size, min = 22, max= 26)
counter <- 1
while(any(A>B)) {
i <- which(A>B)
A[i] <- runif(length(i), min = 19, max= 23)
counter <- counter +1
}
counter
}
plot(x, colMeans(res), log = "x",
xlab ="Size of the data (log scale)", ylab="Expected #iteration")