Как сбалансировать входы с выходами этого ориентированного графа?
Тип графика, о котором я думаю, очень специфичен. Я придумал собственное имя для этого: Iode (ГЛАЗ-ода).
Это игра "I/O" и электроники "анод" и "катод".
МООД
Iode берет несколько элементов из связанных с ним входных узлов и равномерно распределяет элементы по связанным с ним выходным узлам.
- Может быть от 1 до N входных узлов.
- Может быть от 1 до M выходных узлов.
- Ребра из входных узлов объединяются и затем разделяются на выходные узлы.
- Выходные узлы никогда не связаны с входными узлами.
- Когда Iode "тикает", он выполняет операцию балансировки на связанных узлах.
- Максимальный ввод на узел за тик.
- Максимальный выход на узел за тик.
- Максимальная общая пропускная способность на тик.
Вот схема того, как вещи могут быть связаны (используя http://pencil.evolus.vn/): 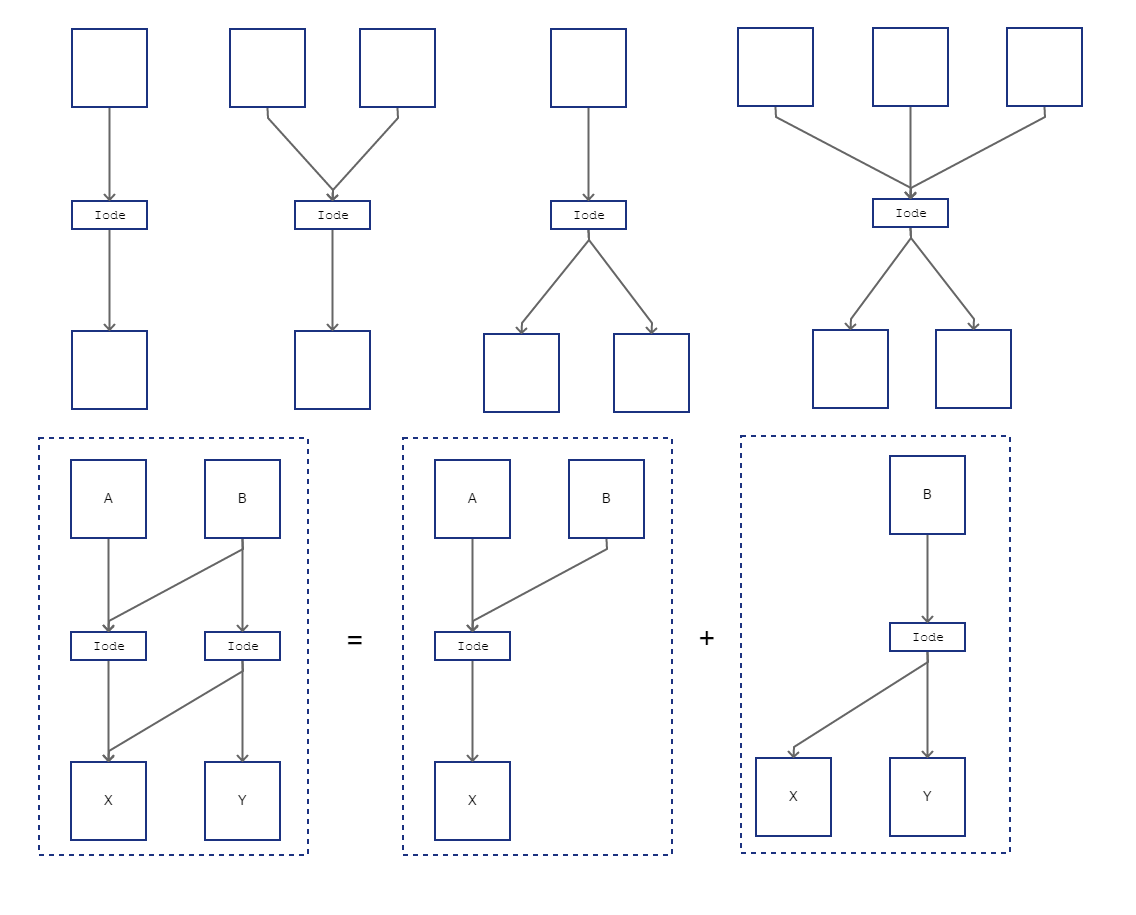
Каждый квадрат - это узел. Каждый узел может содержать некоторое число.
У меня трудности с алгоритмом для тика Iode. Я хочу максимизировать пропускную способность, которая может быть ограничена несколькими способами.
Вот моя первоначальная попытка Python на github ( https://github.com/voxelv/ioder), в частности, в алгоритме:
def iode_int_tick(iode):
# Get the amounts per input iode node
input_amount_per_iode_node = []
for iode_node in iode.input_nodes:
input_amount_per_iode_node.append(min(iode_node.amount, iode.speed['input']))
# Get the amounts per output iode node
output_amount_per_iode_node = []
for iode_node in iode.output_nodes:
output_amount_per_iode_node.append(iode.speed['output'])
# Get the maximum throughput
max_thru_speed = int(iode.speed['throughput'])
input_amount_total = sum(input_amount_per_iode_node)
output_amount_total = sum(output_amount_per_iode_node)
# Compare the maximum throughput
diff_input_thru_max = int(input_amount_total - max_thru_speed)
diff_output_thru_max = int(output_amount_total - max_thru_speed)
# Lessen the input if the maximum throughput is smaller
if diff_input_thru_max > 0:
for i in xrange(len(iode.input_nodes)):
pass # TODO: figure out this
# Lessen the output if the maximum throughput is smaller
if diff_output_thru_max > 0:
for i in xrange(len(iode.input_nodes)):
pass # TODO: figure out this
# Move the numbers from the inputs
for i, inode in enumerate(iode.input_nodes):
inode.take(input_amount_per_iode_node[i])
# Move the numbers into the outputs
for i, inode in enumerate(iode.output_nodes):
inode.give(output_amount_per_iode_node[i])
Я пытаюсь выяснить, что происходит внутри для петель, которые имеют # TODO Комментарии.
Редактировать: пример загружается в main.py и config.py.
Предел ввода на узел 5 Предел выхода на узел 5
Максимальная пропускная способность 8
Таким образом, с двумя входами, установленными на 23 и 6, и двумя выходами, установленными на 4 и 0, ожидаемый результат после тика будет 19 и 2 на входных узлах и 8 и 4 на выходных узлах.
Выполнение кода с python main.py приводит к следующему выводу:
Actual: [18, 1], [9, 5]
Expected: [19, 2], [8, 4]
Еще несколько примеров:
Initial: [22, 2], [3, 20]
Actual: [17, 0], [8, 25]
Expected: [17, 0], [7, 23] or [17, 0], [6, 24]
Ожидаемый может быть одним из упомянутых в зависимости от порядка обработки остатка. Максимальная пропускная способность ограничивает нас до 8, но максимальный ввод на узел ограничивает нас до 5 от первого входного узла. Так как второй входной узел имеет только два, то мы можем предоставить только 7 для этого тика. 7 распределяется по выходам настолько равномерно, насколько это возможно, с 3 или 4 на первом выходе и 4 или 3 на второй выход.
1 ответ
Я придумал аналогию своей проблемы и смог лучше понять ее по аналогии.
Это все равно что пытаться наполнить поднос для кубиков льда водой.
То, как я структурировал Iode, никогда не будет больше воды, чем может выдержать лоток.
Вот мое решение:
def water_into_ice_tray(water, ice_tray, **kwargs):
water_to_put = [0 for _ in xrange(len(ice_tray))]
recursion_ice_tray = [x for x in ice_tray]
# Debug depth
if 'depth' in kwargs:
print kwargs['depth'],
kwargs['depth'] += 1
# BASE_CASE: No more water
if not water > 0:
# Exit early
return water_to_put
# Get slots that have space for more water
open_slots = []
for i in xrange(len(ice_tray)):
if ice_tray[i] > 0:
open_slots.append(i)
# BASE_CASE: Not enough water to go around
if water < len(open_slots):
# Put 1 more in the first 'water' slots
for i in xrange(water):
water_to_put[open_slots[i]] += 1
# Exit early
return water_to_put
# BASE_CASE: Too much water
if water > sum(ice_tray):
raise ValueError("Too much water")
# Attempt to fill each open slot with a distributed amount
fill_amount = int(math.floor(int(water) / len(open_slots)))
leftover = int(water) % len(open_slots)
for slot_index in open_slots:
# With how much water have we overfilled this slot?
diff = fill_amount - ice_tray[slot_index]
if diff >= 0:
# We tried putting too much water into this slot
# Calculate how much to put in it
water_to_put[slot_index] += fill_amount - diff
# No more water can fit into this slot
recursion_ice_tray[slot_index] = 0
# Keep the leftover
leftover += diff
else:
# The slot could hold the water
water_to_put[slot_index] += fill_amount
# Some more water can fit into this slot
recursion_ice_tray[slot_index] = -diff
# None is leftover
# Recurse
recursion_water_to_put = water_into_ice_tray(leftover, recursion_ice_tray, **kwargs)
# Add up recursion result to this result
return map(add, water_to_put, recursion_water_to_put)
def iode_int_tick(iode):
# Calculate available amounts per input node
available_input_per_node = []
for inode in iode.input_nodes:
available_input_per_node.append(min(inode.amount, iode.speed['input']))
input_limit = sum(available_input_per_node)
# Get the throughput
throughput_limit = iode.speed['throughput']
# Calculate available space per output node
available_output_per_node = []
for inode in iode.output_nodes:
available_output_per_node.append(min(inode.max_amount - inode.amount, iode.speed['output']))
output_limit = sum(available_output_per_node)
# Decide which is the limiting factor
limiter = min(input_limit, throughput_limit, output_limit)
if limiter == input_limit:
# If the input limits, then distribute to the outputs. The throughput can handle it.
amount_to_take_per_input_node = available_input_per_node
amount_to_put_per_output_node = water_into_ice_tray(input_limit, available_output_per_node)
pass
elif limiter == throughput_limit:
# If throughput limits, then distribute the throughput amount from the inputs, to the outputs.
amount_to_take_per_input_node = water_into_ice_tray(throughput_limit, available_input_per_node)
amount_to_put_per_output_node = water_into_ice_tray(throughput_limit, available_output_per_node)
pass
elif limiter == output_limit:
# If output limits, then distribute the draw on the inputs. The throughput can handle it.
amount_to_take_per_input_node = water_into_ice_tray(output_limit, available_input_per_node)
amount_to_put_per_output_node = available_output_per_node
pass
else:
raise ValueError("Somehow the limiting factor is something other than the input, throughput, or output.")
# Do the taking
for i in xrange(len(iode.input_nodes)):
iode.input_nodes[i].take(amount_to_take_per_input_node[i])
# Do the giving
for i in xrange(len(iode.output_nodes)):
iode.output_nodes[i].give(amount_to_put_per_output_node[i])