Найти центр (массы) двумерного комплексного многоугольника

Question

Так что мне интересно, каков алгоритм для нахождения центра масс фигур, если у меня есть набор вершин?

Также, если это делает алгоритм короче, мои сложные многоугольники сохраняются как набор простых выпуклых многоугольников, и ты можешь получить их вершины.

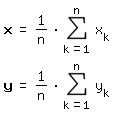
Я нашел вышеприведенное уравнение, но не знаю, как его перевести......

Answer 1

В свете новых доказательств я твердо верю, что ваша формула неверна. Позвольте мне предоставить другой алгоритм. Я пытался сделать так, чтобы это выглядело на C++, но я уверен, что я неправильно понял некоторые вещи. Если вы хотите придираться к этому, это нормально. Если вы хотите понизить их голос, я не могу вас остановить, но я бы предпочел, чтобы вы отредактировали их, чтобы сделать пост лучше.:-)

// use doubles if appropriate
float xsum = 0.0;
float ysum = 0.0;
float area = 0.0;
for(int i = 0; i < points.size - 1; i++) {
    // I'm not a c++ guy... do you need to use pointers? You make the call here
    Point p0 = points[i];
    Point p1 = points[i+1];

    double areaSum = (p0.x * p1.y) - (p1.x * p0.y)

    xsum += (p0.x + p1.x) * areaSum;
    ysum += (p0.y + p1.y) * areaSum;
    area += areaSum;
}

float centMassX = xsum / (area * 6);
float centMassY = ysum / (area * 6);

Answer 2

Попробуйте алгоритм, приведенный здесь. Это будет работать для выпуклых многоугольников.

Answer 3

Общий подход состоит в том, чтобы разбить фигуру на части, для которых расчет проще, рассчитать центры масс для них и объединить их: C= сумма (C[i]* масса [i])/ сумма (масса [i])

Прежде всего вы должны определить, как распределяется масса в многоугольнике. Возможные (простые) распределения:

1. Сосредоточены в вершинах (равномерно) - формулы в вашем вопросе для этого случая
2. Равномерно распределены по границе многоугольника - в этом случае вы должны рассчитать центр масс каждой линии (это просто середина линии), умножить его на длину линии, сложить все и разделить на всю длину границы
3. Равномерно распределены по области многоугольника - самый простой для понимания способ - разбить его на треугольники, вычислить центр масс для каждого из них, умножить на его площадь, сложить все, разделить на всю площадь многоугольника.

Answer 4

Вы можете использовать простую среднюю функцию, примерно так:

template <typename T, typename iterator> T avg(iterator const& begin, iterator const& end) {
  T result;
  size_t size(0);
  for (iterator it = begin; it != end; ++it) {
    result += *it;
    size++;
  }
  return result/size;
}

Теперь, предполагая, что ваши значения находятся в наборе, вы можете сделать:

std::set<double> xs; // assuming your values are in there
double x = avg<double,std::set<double>::iterator>(xs.begin(), xs.end());

Не запустив его через g++, я не уверен, какой из параметров шаблона может быть выведен автоматически.