Многопроцессорная обработка Python: понимание логики `chunksize`
Какие факторы определяют оптимальный chunksize аргумент в пользу таких методов, как multiprocessing.Pool.map()? .map() кажется, что метод использует произвольную эвристику для размера по умолчанию (объяснено ниже); что мотивирует этот выбор и существует ли более продуманный подход, основанный на конкретной ситуации / установке?
Пример - скажи, что я
- Проходя
iterableв.map()это ~15 миллионов элементов; - Работа на машине с 24 ядрами и использование по умолчанию
processes = os.cpu_count()вmultiprocessing.Pool(),
Мое наивное мышление состоит в том, чтобы дать каждому из 24 работников одинаковый размер, т.е. 15_000_000 / 24 или 625 000 Большие куски должны уменьшить текучесть кадров / накладные расходы при полном использовании всех работников. Но, похоже, что здесь отсутствуют некоторые потенциальные недостатки предоставления больших партий каждому работнику. Это неполная картина, и что мне не хватает?
Часть моего вопроса проистекает из логики по умолчанию для chunksize=None: и то и другое .map() а также .starmap() вызов .map_async(), который выглядит так:
def _map_async(self, func, iterable, mapper, chunksize=None, callback=None,
error_callback=None):
# ... (materialize `iterable` to list if it's an iterator)
if chunksize is None:
chunksize, extra = divmod(len(iterable), len(self._pool) * 4) # ????
if extra:
chunksize += 1
if len(iterable) == 0:
chunksize = 0
В чем логика divmod(len(iterable), len(self._pool) * 4)? Это подразумевает, что размер будет ближе к 15_000_000 / (24 * 4) == 156_250, Каково намерение в умножении len(self._pool) на 4?
Это делает размер фрагмента в 4 раза меньше, чем моя "наивная логика" сверху, которая состоит из простого деления длины итерируемого на количество рабочих в pool._pool,
Наконец, есть также этот фрагмент из документации по Python на .imap() что еще больше стимулирует мое любопытство:
chunksizeаргумент такой же, как тот, который используетсяmap()метод. Для очень длинных итераций, используя большое значение дляchunksizeможет сделать работу намного быстрее, чем при использовании значения по умолчанию 1.
Соответствующий ответ, который полезен, но слишком высокоуровневый: многопроцессорность Python: почему большие куски медленнее? ,
3 ответа
Короткий ответ
Алгоритм пула chunksize является эвристическим. Он предоставляет простое решение для всех возможных проблемных сценариев, которые вы пытаетесь внедрить в методы пула. Как следствие, он не может быть оптимизирован для какого-либо конкретного сценария.
Алгоритм произвольно делит итерируемое примерно на четыре раза больше фрагментов, чем наивный подход. Чем больше блоков, тем больше накладных расходов, но повышается гибкость планирования. Как этот ответ покажет, это приводит к более высокой загрузке работника в среднем, но без гарантии более короткого общего времени вычислений для каждого случая.
"Приятно знать, - подумаете вы, - но как знание этого помогает мне в моих конкретных проблемах с многопроцессорностью?" Ну, это не так. Более честный короткий ответ: "короткого ответа нет", "многопроцессорная обработка сложна" и "это зависит". Наблюдаемый симптом может иметь разные корни даже для сходных сценариев.
Этот ответ пытается дать вам основные понятия, помогающие вам получить более четкое представление о черном графике планирования пула. Он также пытается дать вам некоторые базовые инструменты для распознавания и предотвращения потенциальных обрывов, поскольку они связаны с размером кусков.
Об этом ответе
Этот ответ находится в стадии разработки.
Чтобы назвать несколько вещей, которые по-прежнему отсутствуют:
- Итоговый раздел
- Меры по улучшению (кратко) читабельности
Если вам не нужно читать его сейчас, я рекомендую просто пропустить его, чтобы понять, чего ожидать, но отложить проработку, пока эти строки не будут удалены.
Последнее обновление (21 февраля):
- Передал главу 7 в отдельный ответ, потому что я удивился ограничению в 30000 символов
- Добавлены два гифки в главе 7, показывающие пул и простой алгоритм chunksize в действии
Сначала необходимо уточнить некоторые важные термины.
1. Определения
ломоть
Кусок здесь является частью iterable -аргумент, указанный в вызове метода пула. Как вычисляется размер фрагмента и как это может повлиять, - тема этого ответа.
задача
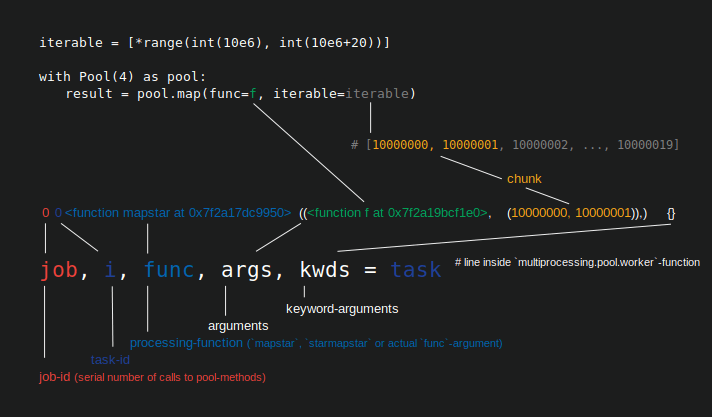
Физическое представление задачи в рабочем процессе в терминах данных можно увидеть на рисунке ниже.
На рисунке показан пример вызова pool.map() отображается вдоль строки кода, взятой из multiprocessing.pool.worker функция, где задача читается из inqueue распаковывается worker является основной основной функцией в MainThread пула-рабочий-процесс. func -аргумент, указанный в методе пула, будет соответствовать только func переменная внутри worker -функция для методов одного вызова, таких как apply_async и для imap с chunksize=1, Для остальных пул-методов с chunksize параметр обработки-функция func будет функцией отображения (mapstar или starmapstar). Эта функция отображает пользовательский func -параметр на каждый элемент передаваемого фрагмента итерируемого (-> "map-tasks"). Время, которое требуется, определяет задачу также как единицу работы.
Taskel
В то время как использование слова "задача" для всей обработки одного блока соответствует коду внутри multiprocessing.pool, нет указаний, как один звонок на указанный пользователем func, с одним элементом блока в качестве аргумента (ов), должны быть упомянуты. Чтобы избежать путаницы, возникающей из-за конфликтов имен maxtasksperchild -параметр внутри пула __init__ -метод), этот ответ будет относиться к отдельным единицам работы в рамках задачи как Taskel.
Задача (из задачи + элемент) - это наименьшая единица работы в задаче. Это однократное выполнение функции, указанной с помощью
func-параметрPool-метод, вызываемый с аргументами, полученными из одного элемента передаваемого фрагмента. Задача состоит изchunksizeTaskels.
Накладные расходы на параллелизацию (PO)
PO состоит из внутренних издержек Python и служебных данных для межпроцессного взаимодействия (IPC). Служебная нагрузка для каждой задачи в Python поставляется с кодом, необходимым для упаковки и распаковки задач и их результатов. Служебная нагрузка IPC сопровождается необходимой синхронизацией потоков и копированием данных между различными адресными пространствами (требуется два шага копирования: parent -> queue -> child). Объем накладных расходов IPC зависит от операционной системы, аппаратного обеспечения и размера данных, что затрудняет обобщение воздействия.
2. Цели распараллеливания
При использовании многопроцессорной обработки нашей общей целью (очевидно) является минимизация общего времени обработки для всех задач. Для достижения этой общей цели нашей технической задачей должна быть оптимизация использования аппаратных ресурсов.
Некоторые важные подцели для достижения технической цели:
- минимизировать издержки распараллеливания (наиболее известный, но не один: IPC)
- высокая загрузка всех процессорных ядер
- ограничение использования памяти для предотвращения чрезмерного подкачки ОС ( очистки)
Сначала задачи должны быть достаточно сложными (интенсивными) в вычислительном отношении, чтобы вернуть ПО, которое мы должны заплатить за распараллеливание. Актуальность ПО уменьшается с увеличением абсолютного времени вычислений на одно задание. Или, другими словами, чем больше абсолютное время вычислений для каждой задачи, тем менее значимой становится потребность в сокращении ПО. Если ваши вычисления займут несколько часов на одну задачу, накладные расходы IPC будут незначительными по сравнению с ними. Основной задачей здесь является предотвращение простоя рабочих процессов после распределения всех задач. Держа все ядра загруженными, значит, мы распараллеливаемся как можно больше.
3. Сценарии распараллеливания
Какие факторы определяют оптимальный аргумент размера фрагмента для таких методов, как multiprocessing.Pool.map()
Основным фактором, о котором идет речь, является то, сколько времени вычислений может варьироваться в зависимости от наших задач. Чтобы назвать это, выбор оптимального размера кусочка определяется...
Коэффициент вариации ( CV) для расчета времени на одно задание.
Два крайних сценария в масштабе, следующие из степени этого изменения:
- Для всех задач требуется одинаковое время вычислений
- Задача может занять несколько секунд или дней
Для лучшей запоминаемости я буду ссылаться на эти сценарии как:
- Плотный сценарий
- Широкий сценарий
Другим определяющим фактором является количество используемых рабочих процессов (при поддержке процессорных ядер). Позже станет понятно почему.
Плотный сценарий
В плотном сценарии было бы желательно распределить все задачи одновременно, чтобы свести к минимуму необходимое IPC и переключение контекста. Это означает, что мы хотим создать только столько кусков, сколько рабочих процессов существует. Как уже указывалось выше, вес ПО увеличивается с меньшими временами вычисления на одно задание.
Для максимальной пропускной способности мы также хотим, чтобы все рабочие процессы были заняты до тех пор, пока не будут выполнены все задачи (без рабочих на холостом ходу). Для этой цели распределенные порции должны быть одинакового размера или близки к.
Широкий сценарий
Основным примером для широкого сценария будет проблема оптимизации, когда результаты либо быстро сходятся, либо вычисления могут занять часы, если не дни. Непредсказуемо, какую смесь "легких задач" и "тяжелых задач" будет содержать задание в таком случае, поэтому не рекомендуется распределять слишком много задач одновременно в пакете задач. Распределение меньшего количества задач одновременно, чем это возможно, означает увеличение гибкости планирования. Это необходимо для достижения нашей подцели высокой эффективности использования всех ядер.
Если Pool методы по умолчанию будут полностью оптимизированы для плотного сценария, они будут все больше создавать неоптимальные временные рамки для каждой проблемы, расположенной ближе к широкому сценарию.
4. Риски Chunksize > 1
Рассмотрим этот упрощенный пример псевдокода с широким сценарием, который мы хотим передать в метод пула:
good_luck_iterable = [60, 60, 86400, 60, 86400, 60, 60, 84600]
Вместо реальных значений мы притворяемся, что видим необходимое время вычисления в секундах, для простоты только 1 минуту или 1 день. Мы предполагаем, что пул состоит из четырех рабочих процессов (на четырех ядрах) и chunksize установлен в 2, Поскольку порядок будет сохранен, куски, отправленные рабочим, будут такими:
[(60, 60), (86400, 60), (86400, 60), (60, 84600)]
Поскольку у нас достаточно рабочих и время вычислений достаточно велико, мы можем сказать, что каждый рабочий процесс получит кусок, над которым он будет работать в первую очередь. (Это не должно иметь место для быстрого выполнения задач). Кроме того, можно сказать, что вся обработка займет около 86400+60 секунд, поскольку это наибольшее общее время вычислений для фрагмента в этом искусственном сценарии, и мы распределяем фрагменты только один раз.
Теперь рассмотрим эту итерацию, в которой переключается только одна позиция по сравнению с предыдущей:
bad_luck_iterable = [60, 60, 86400, 86400, 60, 60, 60, 84600]
... и соответствующие куски:
[(60, 60), (86400, 86400), (60, 60), (60, 84600)]
Просто неудача с сортировкой нашей итерации почти вдвое (86400+86400) нашего общего времени обработки! Рабочий, получивший порочный (86400, 86400)-часть, блокирует вторую тяжелую задачу в своей задаче из-за того, что ее не распределили одному из рабочих на холостом ходу, уже покончившим с (60, 60)-частями. Мы, очевидно, не рискнули бы таким неприятным исходом, если бы установили chunksize=1,
Это риск больших кусков. С более высокими размерами блоков мы торгуем гибкостью планирования за меньшие накладные расходы, и в случаях, как выше, это плохая сделка.
Как мы увидим в главе 6. Количественная оценка эффективности алгоритма, большие размеры фрагментов также могут привести к неоптимальным результатам для плотных сценариев.
5. Алгоритм размера пула
Ниже вы найдете слегка измененную версию алгоритма внутри исходного кода. Как видите, я обрезал нижнюю часть и обернул ее в функцию для вычисления chunksize аргумент внешне. Я тоже заменил 4 с factor параметр и передал на len() звонки.
# mp_utils.py
def calc_chunksize(n_workers, len_iterable, factor=4):
"""Calculate chunksize argument for Pool-methods.
Resembles source-code within `multiprocessing.pool.Pool._map_async`.
"""
chunksize, extra = divmod(len_iterable, n_workers * factor)
if extra:
chunksize += 1
return chunksize
Чтобы убедиться, что мы все на одной странице, вот что divmod делает:
divmod(x, y) это встроенная функция, которая возвращает (x//y, x%y), x // y деление по полу, возвращая округленное вниз число от x / y, в то время как x % y является операцией по модулю, возвращающей остаток от x / y, Отсюда например divmod(10, 3) возвращается (3, 1),
Теперь, когда вы смотрите на chunksize, extra = divmod(len_iterable, n_workers * 4), Вы заметите n_workers вот делитель y в x / y и умножение на 4 без дальнейшей настройки через if extra: chunksize +=1 позже, приводит к начальному размеру куска, по крайней мере, в четыре раза меньше (для len_iterable >= n_workers * 4) чем было бы иначе.
Для просмотра эффекта умножения на 4 на промежуточный результат размера фрагмента рассмотрим следующую функцию:
def compare_chunksizes(len_iterable, n_workers=4):
"""Calculate naive chunksize, Pool's stage-1 chunksize and the chunksize
for Pool's complete algorithm. Return chunksizes and the real factors by
which naive chunksizes are bigger.
"""
cs_naive = len_iterable // n_workers or 1 # naive approach
cs_pool1 = len_iterable // (n_workers * 4) or 1 # incomplete pool algo.
cs_pool2 = calc_chunksize(n_workers, len_iterable)
real_factor_pool1 = cs_naive / cs_pool1
real_factor_pool2 = cs_naive / cs_pool2
return cs_naive, cs_pool1, cs_pool2, real_factor_pool1, real_factor_pool2
Функция выше вычисляет наивный размер фрагмента (cs_naive) и первый шаг размера фрагмента пула алгоритма определения размера фрагмента (cs_pool1), а также размер фрагмента для полного алгоритма пула (cs_pool2). Далее он рассчитывает реальные факторы rf_pool1 = cs_naive / cs_pool1 а также rf_pool2 = cs_naive / cs_pool2, который говорит нам, во сколько раз наивно рассчитанные размеры кусков больше, чем внутренние версии пула.
Ниже вы видите две фигуры, созданные с помощью этой функции. Левый рисунок просто показывает размеры для n_workers=4 вплоть до повторяемой длины 500, На правом рисунке показаны значения для rf_pool1, Для повторяемой длины 16, реальным фактором становится >=4 (за len_iterable >= n_workers * 4) и это максимальное значение 7 для повторяемых длин 28-31, Это огромное отклонение от исходного фактора 4 алгоритм сходится для более длинных итераций. "Более длинный" здесь относительный и зависит от количества указанных работников.
Помните размер cs_pool1 до сих пор не хватает extra -регулировка с остатком от divmod содержалась в cs_pool2 из полного алгоритма.
Алгоритм продолжается с:
if extra:
chunksize += 1
Теперь в случаях, когда есть остаток (extra из операции divmod), увеличение размера фрагмента на 1, очевидно, не может сработать для каждой задачи. В конце концов, если бы это было так, не было бы остатка для начала.
Как вы можете видеть на рисунках ниже, " дополнительная обработка " имеет эффект, что реальный фактор для rf_pool2 сейчас сходится к 4 снизу 4 и отклонение несколько плавнее. Стандартное отклонение для n_workers=4 а также len_iterable=500 падает из 0.5233 за rf_pool1 в 0.4115 за rf_pool2,
В конце концов, увеличение chunksize на 1 приводит к тому, что последнее переданное задание имеет размер len_iterable % chunksize or chunksize,
Чем интереснее и как мы увидим позже, тем больше эффект от дополнительной обработки, тем не менее, можно наблюдать для числа генерируемых кусков (n_chunks). Для достаточно длинных итераций, завершенный алгоритм пула chunksize (n_pool2 на рисунке ниже) стабилизирует количество фрагментов в n_chunks == n_workers * 4, Напротив, наивный алгоритм (после первоначальной отрыжки) продолжает чередоваться между n_chunks == n_workers а также n_chunks == n_workers + 1 как длина повторяемого растет.
Ниже вы найдете две улучшенные информационные функции для пула и простой алгоритм chunksize. Вывод этих функций будет необходим в следующей главе.
# mp_utils.py
from collections import namedtuple
Chunkinfo = namedtuple(
'Chunkinfo', ['n_workers', 'len_iterable', 'n_chunks',
'chunksize', 'last_chunk']
)
def calc_chunksize_info(n_workers, len_iterable, factor=4):
"""Calculate chunksize numbers."""
chunksize, extra = divmod(len_iterable, n_workers * factor)
if extra:
chunksize += 1
# `+ (len_iterable % chunksize > 0)` exploits that `True == 1`
n_chunks = len_iterable // chunksize + (len_iterable % chunksize > 0)
# exploit `0 == False`
last_chunk = len_iterable % chunksize or chunksize
return Chunkinfo(
n_workers, len_iterable, n_chunks, chunksize, last_chunk
)
Не смущайтесь, возможно, неожиданным взглядом calc_naive_chunksize_info, extra от divmod не используется для расчета размера фрагмента.
def calc_naive_chunksize_info(n_workers, len_iterable):
"""Calculate naive chunksize numbers."""
chunksize, extra = divmod(len_iterable, n_workers)
if chunksize == 0:
chunksize = 1
n_chunks = extra
last_chunk = chunksize
else:
n_chunks = len_iterable // chunksize + (len_iterable % chunksize > 0)
last_chunk = len_iterable % chunksize or chunksize
return Chunkinfo(
n_workers, len_iterable, n_chunks, chunksize, last_chunk
)
6. Количественная оценка эффективности алгоритма
Теперь, когда мы увидели, как вывод Pool Алгоритм chunksize выглядит иначе по сравнению с выводом из наивного алгоритма...
- Как определить, действительно ли подход пула что-то улучшает?
- И что именно это может быть?
Как показано в предыдущей главе, для более длинных итераций (большее число задач) алгоритм пула chunksize-алгоритм приблизительно делит итерируемое на четыре раза больше фрагментов, чем наивный метод. Меньшие куски означают больше задач, а больше задач - больше издержек распараллеливания (PO), затраты, которые должны быть сопоставлены с преимуществом повышенной гибкости планирования (вспомните "Риски Chunksize > 1").
По довольно очевидным причинам основной алгоритм пула chunksize не может сопоставить гибкость планирования с ПО для вас. Издержки IPC зависят от операционной системы, аппаратного обеспечения и размера данных. Алгоритм не может знать, на каком оборудовании мы запускаем наш код, и не имеет понятия, сколько времени займет выполнение задачи. Это эвристическое обеспечение основных функций для всех возможных сценариев. Это означает, что он не может быть оптимизирован для какого-либо конкретного сценария. Как упоминалось ранее, ПО также становится все менее важной для увеличения времени вычислений на одно задание (отрицательная корреляция).
Когда вы вспоминаете Цели распараллеливания из главы 2, одним из пунктов было следующее:
- высокая загрузка всех процессорных ядер
Повторяющийся вопрос о SO относительно multiprocessing.Pool спрашивают люди, интересующиеся неиспользуемыми ядрами / простоями рабочих процессов в ситуациях, когда можно ожидать, что все рабочие процессы заняты.
Бездействие рабочих процессов ближе к концу нашего вычисления - это наблюдение, которое мы можем сделать даже с помощью плотных сценариев (полностью равных времени вычислений на одно задание) в тех случаях, когда число работников не является делителем числа кусков (n_chunks % n_workers > 0).
Большее количество кусков означает повышенную вероятность того, что число работников будет делителем для n_chunks следовательно, соответственно увеличивается вероятность не наблюдать за работающими на холостом ходу работниками.
По причинам, упомянутым ранее, аспект ПО полностью выходит за рамки теоретических соображений об измерении эффективности алгоритма, по крайней мере, на начальном этапе. Вышеупомянутый алгоритм пула chunksize-алгоритм, который можно попытаться улучшить, - это минимизация холостых рабочих процессов и, соответственно, использование процессорных ядер.
Значение, определяющее коэффициент использования работника, я буду называть:
Эффективность распараллеливания (PE)
Нашим исходным условием формализации проблемы, стабильным состоянием, является плотный сценарий с абсолютно равными временами вычислений на одно задание. Любой другой сценарий был бы случайным / хаосом и не подходил для расследования при прочих равных условиях. Другие факторы хаоса, такие как политика планирования потоков ОС, также не принимаются во внимание.
Важно отметить, что PE в том смысле, в котором я здесь использую этот термин, не коррелирует автоматически с более быстрым общим вычислением для данной проблемы распараллеливания. PE не сообщает нам, заняты ли работники продуктивно, или большую часть времени тратится на обработку накладных расходов. Он только говорит нам процент использования работника в смысле отсутствия работающих на холостом ходу - и это только для нашей упрощенной модели.
6.1 Абсолютная эффективность распараллеливания (APE)
Размышляя о том, как бы я мог на самом деле количественно оценить возможное преимущество алгоритма chunksize для пула по сравнению с наивным алгоритмом chunksize-алгоритма, я представил картину рабочего планирования пула, как вы видите ее ниже.
- Ось X разделена на равные единицы времени, где каждая единица соответствует времени вычисления, которое требуется для задачи.
- Ось Y делится на количество рабочих процессов, которые использует пул.
- Задача здесь отображается как наименьший прямоугольник голубого цвета, помещенный во временную шкалу (график) анонимного рабочего процесса.
- Задача - это одна или несколько задач на рабочем графике, которые постоянно выделяются одним и тем же оттенком.
- Единицы времени холостого хода представлены красным цветом.
- Параллельное расписание разбито на разделы. Последний раздел является хвостовой частью.
Названия составных частей можно увидеть на картинке ниже.
Эффективность распараллеливания затем рассчитывается путем деления занятой доли на весь потенциал:
Абсолютная эффективность распараллеливания (APE) = занятая доля / параллельное расписание
Вот как это выглядит в коде:
# mp_utils.py
def calc_abs_pe(n_workers, len_iterable, n_chunks, chunksize, last_chunk):
"""Calculate absolute parallelization efficiency.
`len_iterable` is not used, but contained to keep a consistent signature
with `calc_rel_pe`.
"""
potential = (
((n_chunks // n_workers + (n_chunks % n_workers > 1)) * chunksize)
+ (n_chunks % n_workers == 1) * last_chunk
) * n_workers
n_full_chunks = n_chunks - (chunksize > last_chunk)
taskels_in_regular_chunks = n_full_chunks * chunksize
real = taskels_in_regular_chunks + (chunksize > last_chunk) * last_chunk
abs_pe = real / potential
return abs_pe
Если доля холостого хода отсутствует, занятая доля будет равна параллельному расписанию, поэтому мы получаем APE в размере 100%. В нашей упрощенной модели это сценарий, в котором все доступные процессы будут заняты все время, необходимое для обработки всех задач. Другими словами, вся работа эффективно распределяется до 100 процентов.
Но почему я продолжаю называть PE абсолютным PE здесь?
Чтобы понять это, мы должны рассмотреть возможный случай для размера фрагмента (cs), который обеспечивает максимальную гибкость планирования (также, число Горцев может быть. Совпадение?):
___________________________________ ~ ONE ~ ___________________________________
Например, если у нас будет четыре рабочих процесса и 37 задач, рабочие будут работать на холостом ходу даже при chunksize=1, просто так n_workers=4 не делитель 37. Остальная часть деления 37 / 4 равна 1. Эту единственную оставшуюся задачу придется обрабатывать одному работнику, а остальные три - на холостом ходу.
Кроме того, еще будет один рабочий на холостом ходу с 39 задачами, как вы можете видеть на рисунке ниже.
Когда вы сравниваете верхний параллельный график для chunksize=1 с приведенной ниже версией для chunksize=3, вы заметите, что верхнее параллельное расписание меньше, временная шкала на оси X короче. Теперь должно стать очевидным, как неожиданно большие куски также могут привести к увеличению общего времени вычислений даже для плотных сценариев.
Но почему бы просто не использовать длину оси X для расчетов эффективности?
Потому что накладные расходы не содержатся в этой модели. Это будет отличаться для обоих кусков, следовательно, ось X не является прямо сопоставимой. Затраты по-прежнему могут привести к увеличению общего времени вычислений, как показано в случае 2 на рисунке ниже.
6.2 Относительная эффективность распараллеливания (RPE)
Значение APE не содержит информацию о том, возможно ли лучшее распределение задач с размером фрагмента, равным 1. Лучшее значение здесь по-прежнему означает меньшую долю холостого хода.
Чтобы получить значение PE, скорректированное на максимально возможное значение PE, мы должны разделить рассматриваемый APE на APE, с которым мы получаем chunksize=1,
Относительная эффективность распараллеливания (RPE) = APE_cs_x / APE_cs_1
Вот как это выглядит в коде:
# mp_utils.py
def calc_rel_pe(n_workers, len_iterable, n_chunks, chunksize, last_chunk):
"""Calculate relative parallelization efficiency."""
abs_pe_cs1 = calc_abs_pe(
n_workers, len_iterable, n_chunks=len_iterable,
chunksize=1, last_chunk=1
)
abs_pe = calc_abs_pe(
n_workers, len_iterable, n_chunks, chunksize, last_chunk
)
rel_pe = abs_pe / abs_pe_cs1
return rel_pe
RPE, как здесь определено, по сути является рассказом о хвосте параллельного расписания. На RPE влияет максимально эффективный размер кусочка, содержащийся в хвосте. (Этот хвост может иметь длину оси X chunksize или же last_chunk.) Это имеет следствие, что RPE естественно сходится к 100% (даже) для всех видов "хвостов", как показано на рисунке ниже.
Низкий RPE...
- является сильным намеком на потенциал оптимизации.
- естественно, становится менее вероятным для более длинных итераций, потому что относительная хвостовая часть общего параллельного расписания сокращается.
найдите часть II этого ответа ниже.
Об этом ответе
Этот ответ находится в стадии разработки. В настоящее время он рассматривается как часть II принятого ответа выше, потому что я удивился ограничению в 30000 символов, которое, по-видимому, имеет SO.
7. Наивный и пульный алгоритм.
Прежде чем углубляться в детали, рассмотрим две картинки ниже. Для ряда разных iterable длины, они показывают, как два сравниваемых алгоритма разделяют пройденный iterable (это будет последовательность к тому времени) и как распределенные в результате задачи могут быть распределены. Порядок работников является случайным, и количество распределенных задач на одного работника в действительности может отличаться от этого изображения для легких задач и / или задач в широком сценарии. Как упоминалось ранее, накладные расходы также не включены сюда. Однако для достаточно тяжелых задач в плотном сценарии с пренебрежимо малым размером передаваемых данных реальные вычисления дают очень похожую картину.
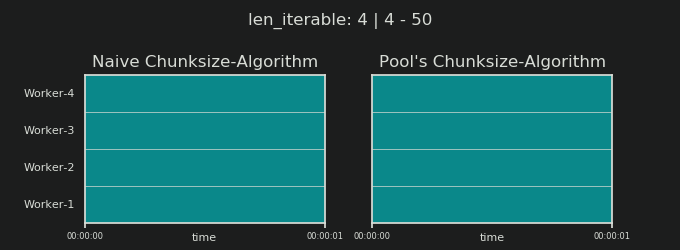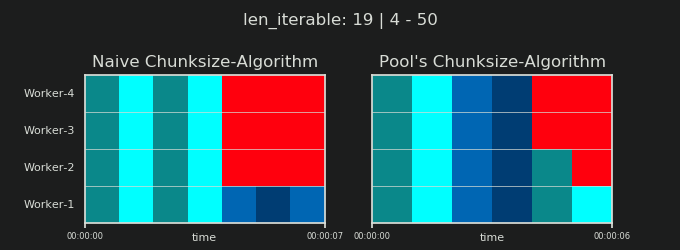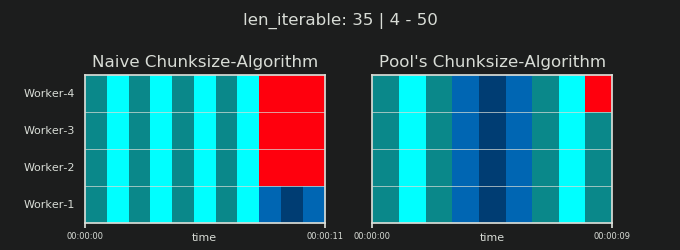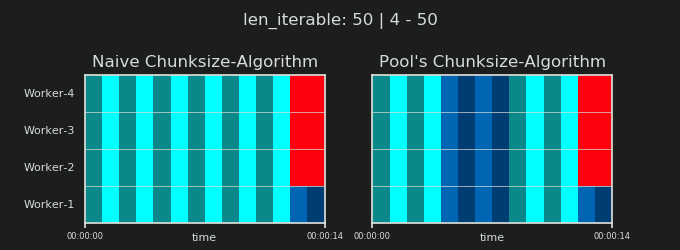
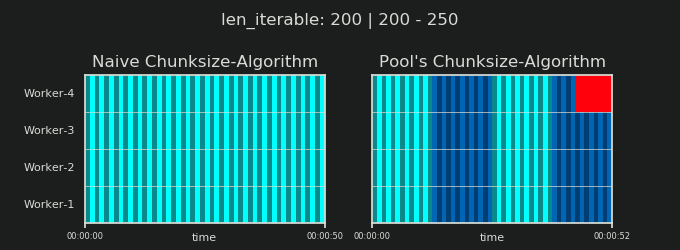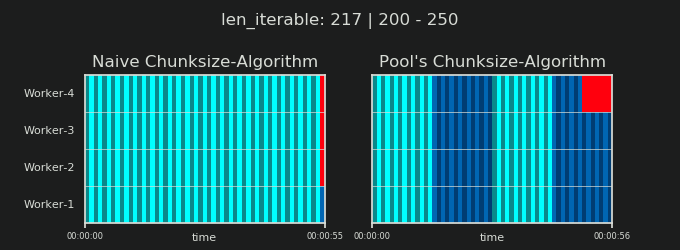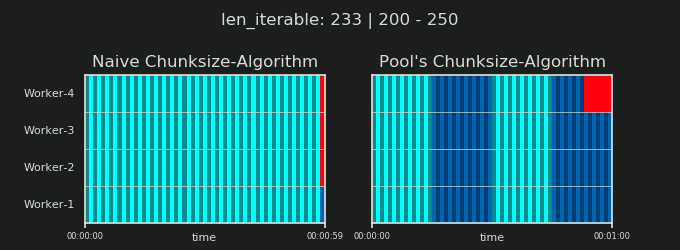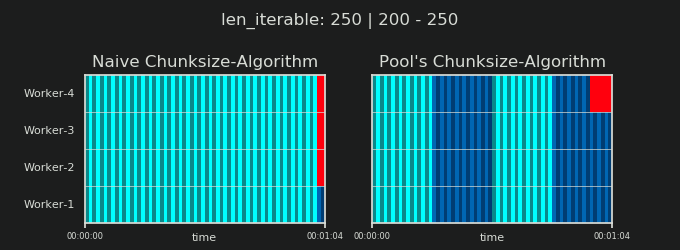
Как показано в главе " 5. Алгоритм размера пула ", при использовании алгоритма размера пула число чанков стабилизируется на уровне n_chunks == n_workers * 4 для достаточно больших итераций, в то время как он продолжает переключаться между n_chunks == n_workers а также n_chunks == n_workers + 1 с наивным подходом. Для наивного алгоритма, потому что n_chunks % n_workers == 1 является True за n_chunks == n_workers + 1, это имеет драматический эффект, что будет создан новый раздел, где работает только один работник.
Наивный Chunksize-Алгоритм:
Вы можете подумать, что вы создали задачи с одинаковым количеством рабочих, но это будет справедливо только в тех случаях, когда нет остатка для
len_iterable / n_workers, Если есть остаток, будет новый раздел только с одной задачей для одного работника. В этот момент ваши вычисления больше не будут параллельными.
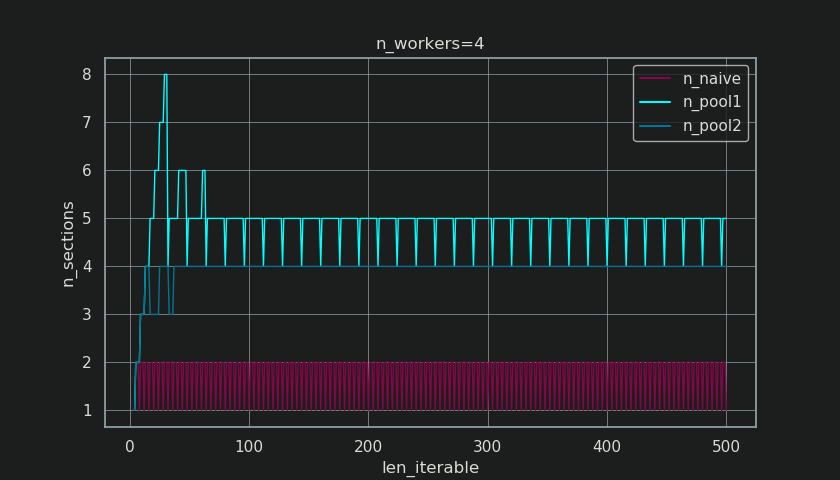
Ниже вы видите фигуру, аналогичную показанной в главе 5, но показывающую количество секций вместо количества фрагментов. Для полного алгоритма chunksize пула (n_pool2), n_sections стабилизируется при печально известном, жестко закодированном факторе 4, Для наивного алгоритма, n_sections будет чередоваться от одного до двух.
Для алгоритма chunksize пула стабилизация при n_chunks = n_workers * 4 благодаря вышеупомянутой дополнительной обработке предотвращает создание нового раздела и ограничивает общий ресурс холостого хода одним рабочим в течение достаточно продолжительного времени. Кроме того, алгоритм будет продолжать сокращать относительный размер доли холостого хода, что приводит к значению RPE, приближающемуся к 100%.
"Достаточно долго" для n_workers=4 является len_iterable=210 например. Для итераций, равных или больших, доля холостого хода будет ограничена одним рабочим.
Наивный алгоритм уменьшения размера также сходится к 100%, но это происходит медленнее. Сходящийся эффект зависит исключительно от того, что относительная часть хвоста сжимается для случаев, когда будет две секции. Этот хвост только с одним занятым работником ограничен длиной оси X n_workers - 1, возможный максимальный остаток для len_iterable / n_workers,
Как фактические значения RPE различаются для наивного алгоритма и пула chunksize-алгоритма?
Ниже вы найдете две тепловые карты, показывающие значения RPE для всех повторяемых длин до 5000, для всех чисел рабочих от 2 до 100. Цветовая шкала варьируется от 0,5 до 1 (50%-100%). Вы заметите намного больше темных областей (более низкие значения RPE) для наивного алгоритма в левой тепловой карте. Алгоритм пула chunksize, напротив, рисует более солнечную картину.
Диагональный градиент нижних левых темных углов по сравнению с правыми верхними светлыми углами снова показывает зависимость от числа рабочих для того, что можно назвать "длинным итеративным".
Насколько плохо это может быть с каждым алгоритмом?
С помощью алгоритма chunksize пула RPE 81,25 % является самым низким значением для диапазона рабочих и повторяемых длин, указанных выше:
С наивным алгоритмом chunksize все может стать намного хуже. Самый низкий рассчитанный RPE здесь составляет 50,72 %. В этом случае почти на половину времени вычислений работает только один рабочий! Итак, берегитесь, гордые обладатели Knights Landing.;)
наступающие: заключительные примечания
Я думаю, что отчасти вам не хватает того, что ваша наивная оценка предполагает, что каждая единица работы занимает одинаковое количество времени, и в этом случае ваша стратегия будет наилучшей. Но если некоторые задания завершаются раньше, чем другие, некоторые ядра могут простаивать в ожидании завершения медленных заданий.
Таким образом, разбивая фрагменты на 4 раза больше частей, тогда, если один блок закончился рано, это ядро может запустить следующий блок (в то время как другие ядра продолжают работать над их более медленным блоком).
Я не знаю, почему они выбрали фактор 4 точно, но это было бы компромиссом между минимизацией накладных расходов кода карты (который требует наибольшего возможного количества чанков) и балансировкой чанков, занимающих различное количество раз (что требует наименьшего возможного чанка)).