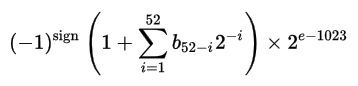Почему 24,0000 не равно 24,0000 в MATLAB?
Я пишу программу, в которой мне нужно удалить дубликаты точек, хранящиеся в матрице. Проблема состоит в том, что когда дело доходит до проверки, находятся ли эти точки в матрице, MATLAB не может распознать их в матрице, хотя они существуют.
В следующем коде intersections Функция получает точки пересечения:
[points(:,1), points(:,2)] = intersections(...
obj.modifiedVGVertices(1,:), obj.modifiedVGVertices(2,:), ...
[vertex1(1) vertex2(1)], [vertex1(2) vertex2(2)]);
Результат:
>> points
points =
12.0000 15.0000
33.0000 24.0000
33.0000 24.0000
>> vertex1
vertex1 =
12
15
>> vertex2
vertex2 =
33
24
Две точки (vertex1 а также vertex2) следует исключить из результата. Это должно быть сделано с помощью следующих команд:
points = points((points(:,1) ~= vertex1(1)) | (points(:,2) ~= vertex1(2)), :);
points = points((points(:,1) ~= vertex2(1)) | (points(:,2) ~= vertex2(2)), :);
После этого мы получили неожиданный результат:
>> points
points =
33.0000 24.0000
Результатом должна быть пустая матрица. Как видите, первая (или вторая?) Пара [33.0000 24.0000] был устранен, но не второй.
Затем я проверил эти два выражения:
>> points(1) ~= vertex2(1)
ans =
0
>> points(2) ~= vertex2(2)
ans =
1 % <-- It means 24.0000 is not equal to 24.0000?
В чем проблема?
Что еще более удивительно, я сделал новый скрипт, который имеет только эти команды:
points = [12.0000 15.0000
33.0000 24.0000
33.0000 24.0000];
vertex1 = [12 ; 15];
vertex2 = [33 ; 24];
points = points((points(:,1) ~= vertex1(1)) | (points(:,2) ~= vertex1(2)), :);
points = points((points(:,1) ~= vertex2(1)) | (points(:,2) ~= vertex2(2)), :);
Результат как и ожидалось:
>> points
points =
Empty matrix: 0-by-2
6 ответов
Ваша проблема связана с тем, как числа с плавающей точкой представлены на компьютере. Более подробное обсуждение представлений с плавающей точкой появляется в конце моего ответа (раздел "Представление с плавающей точкой"). Версия TL;DR: поскольку компьютеры имеют ограниченный объем памяти, числа могут быть представлены только с конечной точностью. Таким образом, точность чисел с плавающей запятой ограничена определенным количеством десятичных знаков (около 16 значащих цифр для значений двойной точности, по умолчанию используется в MATLAB).
Фактическая и отображаемая точность
Теперь обратимся к конкретному примеру в вопросе... пока 24.0000 а также 24.0000 отображаются одинаково, получается, что они на самом деле отличаются очень маленькими десятичными величинами в этом случае. Вы этого не видите, потому что MATLAB по умолчанию отображает только 4 значащие цифры, сохраняя общее отображение в чистоте и порядке. Если вы хотите увидеть полную точность, вы должны либо выпустить format long введите команду или просмотрите шестнадцатеричное представление числа:
>> pi
ans =
3.1416
>> format long
>> pi
ans =
3.141592653589793
>> num2hex(pi)
ans =
400921fb54442d18
Инициализированные значения против вычисленных значений
Поскольку существует только конечное число значений, которые могут быть представлены для числа с плавающей запятой, вычисление может привести к значению, которое попадает между двумя из этих представлений. В таком случае результат должен быть округлен до одного из них. Это вносит небольшую ошибку точности машины. Это также означает, что инициализация значения напрямую или с помощью некоторых вычислений может дать немного другие результаты. Например, значение 0.1 не имеет точного представления с плавающей запятой (то есть оно слегка округляется), и поэтому вы в итоге получите нелогичные результаты, подобные этому, из-за способа накопления ошибок округления:
>> a=sum([0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1]); % Sum 10 0.1s
>> b=1; % Initialize to 1
>> a == b
ans =
logical
0 % They are unequal!
>> num2hex(a) % Let's check their hex representation to confirm
ans =
3fefffffffffffff
>> num2hex(b)
ans =
3ff0000000000000
Как правильно обрабатывать сравнения с плавающей точкой
Поскольку значения с плавающей запятой могут отличаться на очень небольшие величины, любые сравнения должны выполняться путем проверки того, что значения находятся в некотором диапазоне (т.е. допуска) друг от друга, а не в точности равны друг другу. Например:
a = 24;
b = 24.000001;
tolerance = 0.001;
if abs(a-b) < tolerance, disp('Equal!'); end
будет отображаться "Равно!".
Затем вы можете изменить свой код на что-то вроде:
points = points((abs(points(:,1)-vertex1(1)) > tolerance) | ...
(abs(points(:,2)-vertex1(2)) > tolerance),:)
Представление с плавающей точкой
Хороший обзор чисел с плавающей точкой (и, в частности, стандарта IEEE 754 для арифметики с плавающей точкой) - " Что должен знать каждый компьютерный ученый об арифметике с плавающей точкой " Дэвида Голдберга.
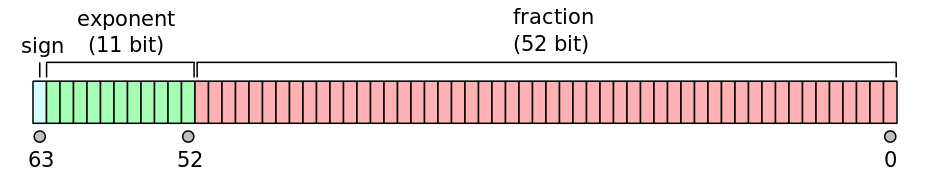
Двоичное число с плавающей запятой фактически представлено тремя целыми числами: знаковый бит s, значение и (или коэффициент / дробь) b и показатель e, Для формата с плавающей запятой двойной точности каждое число представлено 64 битами, расположенными в памяти следующим образом:
Затем можно найти действительное значение по следующей формуле:
Этот формат допускает представления чисел в диапазоне от 10^-308 до 10^308. Для MATLAB вы можете получить эти ограничения от realmin а также realmax:
>> realmin
ans =
2.225073858507201e-308
>> realmax
ans =
1.797693134862316e+308
Поскольку существует конечное число битов, используемых для представления числа с плавающей запятой, существует только так много конечных чисел, которые могут быть представлены в указанном выше диапазоне. Вычисления часто приводят к значению, которое точно не соответствует одному из этих конечных представлений, поэтому значения должны быть округлены. Эти ошибки машинной точности проявляются по-разному, как обсуждалось в приведенных выше примерах.
Чтобы лучше понять эти ошибки округления, полезно взглянуть на относительную точность с плавающей точкой, обеспечиваемую функцией eps, который количественно определяет расстояние от заданного числа до следующего по величине представления с плавающей точкой:
>> eps(1)
ans =
2.220446049250313e-16
>> eps(1000)
ans =
1.136868377216160e-13
Обратите внимание, что точность зависит от размера представляемого числа; большие числа будут иметь большие расстояния между представлениями с плавающей точкой и, следовательно, будут иметь меньше цифр точности после десятичной точки. Это может быть важным соображением с некоторыми расчетами. Рассмотрим следующий пример:
>> format long % Display full precision
>> x = rand(1, 10); % Get 10 random values between 0 and 1
>> a = mean(x) % Take the mean
a =
0.587307428244141
>> b = mean(x+10000)-10000 % Take the mean at a different scale, then shift back
b =
0.587307428244458
Обратите внимание, что когда мы сдвигаем значения x из диапазона [0 1] к диапазону [10000 10001], вычислите среднее значение, затем вычтите среднее смещение для сравнения, мы получим значение, которое отличается для последних 3 значащих цифр. Это иллюстрирует, как смещение или масштабирование данных может изменить точность вычислений, выполненных с ними, что необходимо учитывать при определенных проблемах.
Посмотрите на эту статью: Опасности с плавающей точкой. Хотя его примеры на FORTRAN, он имеет смысл практически для любого современного языка программирования, включая MATLAB. Ваша проблема (и решение для нее) описана в разделе "Безопасные сравнения".
Тип
format long g
Эта команда покажет ПОЛНОЕ значение числа. Это может быть что-то вроде 24.00000021321!= 24.00000123124
Попробуйте написать
0,1 + 0,1 + 0,1 == 0,3.
Предупреждение: вы можете быть удивлены результатом!
Возможно, эти два числа действительно 24,0 и 24,000000001, но вы не видите все десятичные знаки.
Проверьте функцию Matlab EPS.
Matlab использует математику с плавающей запятой с точностью до 16 цифр (отображается только 5).