R: площадь под кривой ogive?

Question

У меня есть алгоритм, который использует график x,y отсортированных данных y, чтобы произвести ogive.

Затем я получаю площадь под кривой, чтобы вывести%.

Я хотел бы сделать что-то подобное, используя оценку плотности ядра. Мне нравится, как верхние / нижние границы сглаживаются с помощью плотностей ядра (то есть минимальное и максимальное значения немного выходят за пределы моего жестко запрограммированного ввода).

В любом случае... Мне было интересно, есть ли способ трактовать ogive как тип кумулятивной функции распределения и / или использовать оценку плотности ядра для получения кумулятивной функции распределения по данным y?

Я прошу прощения, если это запутанный вопрос. Я знаю, что есть способ получить кумулятивный график частоты (т. Е. Ogive). Тем не менее, я не могу определить, как получить%, учитывая этот график накопленной частоты.

Чего я не хочу, так это ecdf. Я знаю, как это сделать, и я не совсем пытаюсь записать ecdf. Но, скорее, интеграция ogive с учетом двух интервалов.

Answer 1

Я не совсем уверен, что вы имеете в виду, но вот способ вычислить площадь под кривой для оценки плотности ядра (или, в более общем случае, для любого случая, когда у вас есть значения y при одинаково разнесенных значениях x (хотя вы можно, конечно, обобщать и на переменные x интервалы)):

library(zoo)

# Kernel density estimate
# Set n to higher value to get a finer grid
set.seed(67839)
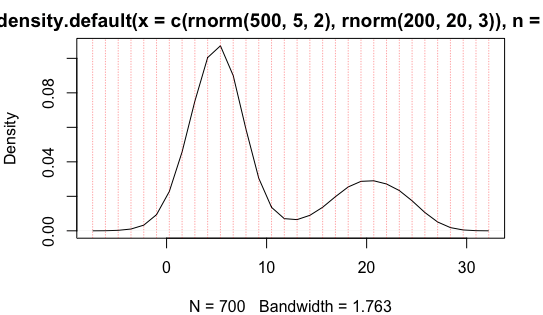
dens = density(c(rnorm(500,5,2),rnorm(200,20,3)), n=2^5)

# How to extract the x and y values of the density estimate
#dens$y
#dens$x

# x interval
dx = median(diff(dens$x))

# mean height for each pair of y values
h = rollmean(dens$y, 2)

# Area under curve
sum(h*dx)  # 1.000943

# Cumulative area
# cumsum(h*dx)

# Plot density, showing points at which density is calculated 
plot(dens)
abline(v=dens$x, col="#FF000060", lty="11")

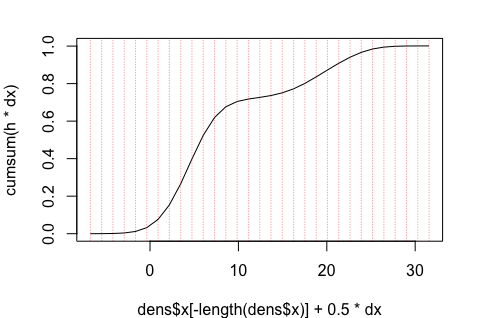
# Plot cumulative area under curve, showing mid-point of each x-interval
plot(dens$x[-length(dens$x)] + 0.5*dx, cumsum(h*dx), type="l")
abline(v=dens$x[-length(dens$x)] + 0.5*dx, col="#FF000060", lty="11")

ОБНОВЛЕНИЕ, чтобы включить ecdf функция

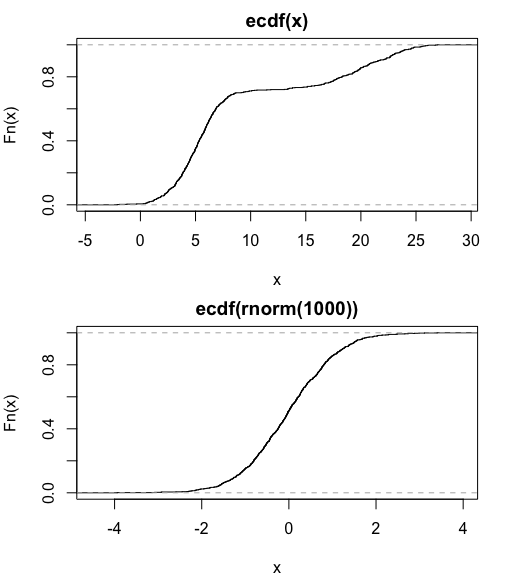
Чтобы ответить на ваши комментарии, посмотрите на два графика ниже. Первая - это эмпирическая кумулятивная функция распределения (ECDF) смеси нормальных распределений, которую я использовал выше. Обратите внимание, что график этих данных выглядит так же, как и выше. Второе - график ECDF простого ванильного нормального распределения, среднее =0, sd=1.

set.seed(67839)
x = c(rnorm(500,5,2),rnorm(200,20,3))
plot(ecdf(x), do.points=FALSE)

plot(ecdf(rnorm(1000)))