Я с переменным для повторных мер
Я столкнулся со странными результатами при использовании Ime с повторными измерениями и VarIdent. Любая помощь с этим будет очень признательна!
Я проверяю, отличается ли сигнал 13C листьев по временному ряду между двумя видами (A и B). Меня в основном интересуют общие различия между видами, а не конкретные моменты времени.
Вот мой набор данных:
Block Species time X13C
1 B 2 0.775040865
2 B 2 0.343913792
3 B 2 0.381053614
1 A 2 0.427101597
2 A 2 0.097743662
3 A 2 0.748345826
1 B 24 0.416700446
2 B 24 0.230773558
3 B 24 0.681386484
1 A 24 0.334026511
2 A 24 0.866426406
3 A 24 0.606346215
1 B 48 0.263085491
2 B 48 0.083323709
3 B 48 0.534697801
1 A 48 0.30594443
2 A 48 0.024555489
3 A 48 0.790670392
1 B 96 0.158090804
2 B 96 0.254880689
3 B 96 0.082666799
1 A 96 0.139189281
2 A 96 0.300340119
3 A 96 0.233149535
1 B 192 0.055421148
2 B 192 0.082582155
3 B 192 0.136636735
1 A 192 0.03641637
2 A 192 0.06082544
3 A 192 0.126029308
Я применяю следующую модель:
bulk<-lme(X13Catex ~ Species*time, random = ~1|Block/Species, method='REML', na.action=na.exclude, data=VacL, corAR1())
Поскольку существует разнородность невязок по времени, я применил varIdent, который улучшил подгонку модели (AIC). Нормализованные участки остатков также выглядели хорошо.
bulk.var<-lme(X13Catex ~ Species*time, random = ~1|Block/Species, method='REML', na.action=na.exclude, data=VacL, corAR1(), weights=varIdent(form=~1|time))
Дело в том, что с помощью этого кода я получаю значительное значение p для видов, но, глядя на мои данные, кажется, что виды вообще не различаются... Я думаю, что очень странно получить такое низкое значение p, так как Столбики ошибок перекрываются в каждый момент времени, а также в некоторые моменты времени A больше, чем B, а в некоторых других наоборот.
> anova(bulk.var)
numDF denDF F-value p-value
(Intercept) 1 15 13.25772 0.0024
SpeciesCode 1 2 67.08281 0.0146
SamplingTime 4 15 4.42320 0.0147
SpeciesCode:SamplingTime 4 15 1.27659 0.3227
Это случилось снова, когда я проанализировал другие подобные переменные...
Интересно, может ли быть проблема с низкой репликацией для каждого вида в каждый момент отбора проб (n = 3). Может ли быть так, что применение varIdent и "относительно сложной" модели с таким низким количеством повторов объясняет найденное значимое значение p? Любые предложения о том, как с этим бороться?
Спасибо!!
1 ответ
ОК, дай мне попробовать.
Прежде всего, ваша корреляционная структура не кажется мне правильной. Вам нужно использовать ковариату времени там.
fit0 <- lme(X13C ~ Species*time, random = ~1|Block/Species, method='REML',
na.action=na.exclude, data=VacL,
corAR1(0.9, form = ~ time | Block/Species))
summary(fit0)
Тогда дисперсия вложенного случайного эффекта представляется довольно малой. Попробуем убрать этот параметр.
fit1 <- lme(X13C ~ Species*time, random = ~1|Block, method='REML',
na.action=na.exclude, data=VacL,
corAR1(0.9, form = ~ time | Block/Species))
summary(fit1)
anova(fit0, fit1)
# Model df AIC BIC logLik Test L.Ratio p-value
#fit0 1 8 35.47003 45.5348 -9.735014
#fit1 2 7 33.47003 42.2767 -9.735014 1 vs 2 8.37192e-09 0.9999
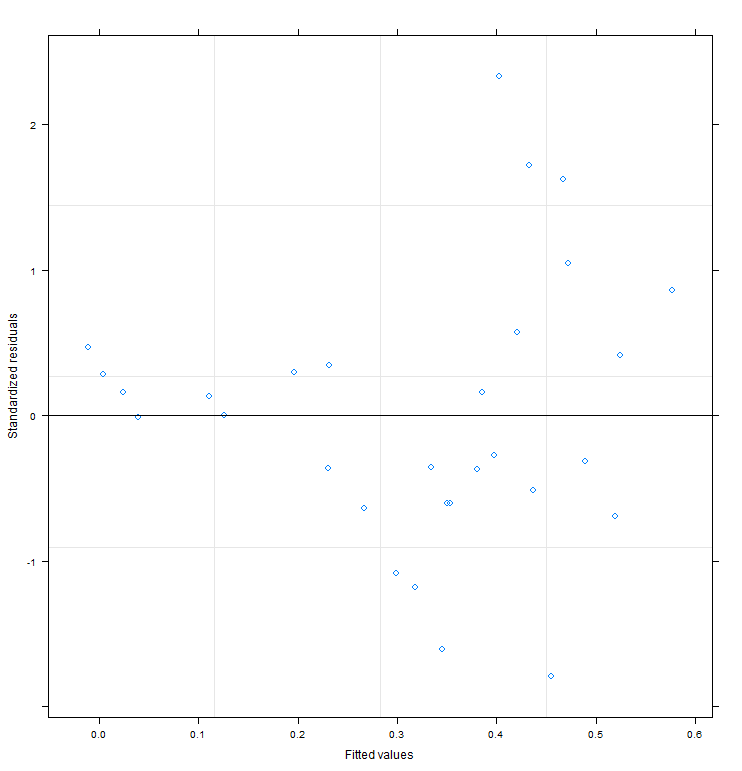
plot(fit1)
Сюжет действительно показывает сильную неоднородность. На данный момент я бы серьезно подумал о GLMM. Помните, дельта 13 C - это (преобразованная) фракция 13C/12C. Предположение о нормальности кажется немного сомнительным для этого (хотя я иногда использую его для дельта-значений сам). Однако мне кажется, что мы можем смоделировать дисперсию в зависимости от подобранных значений.
fit2 <- lme(X13C ~ Species*time, random = ~1|Block, method='REML',
na.action=na.exclude, data=VacL,
corAR1(0.9, form = ~ time | Block/Species),
weights = varPower())
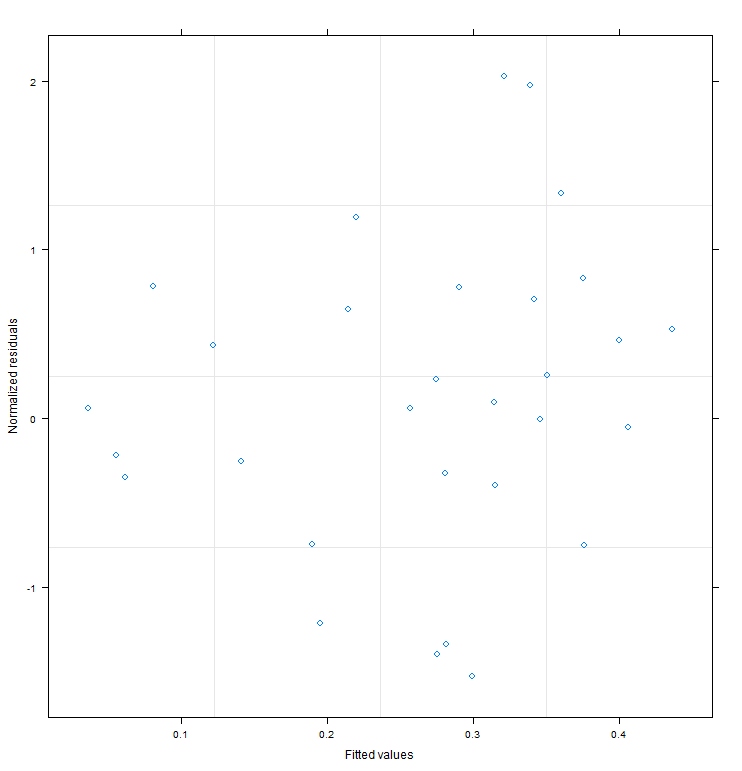
plot(fit2, resid(., type = "normalized") ~ fitted(.))
anova(fit1, fit2)
# Model df AIC BIC logLik Test L.Ratio p-value
#fit1 1 7 33.47003 42.27670 -9.735014
#fit2 2 8 11.34319 21.40796 2.328405 1 vs 2 24.12684 <.0001
Не так уж плохо. Давайте проверим p-значения.
coef(summary(fit2))
# Value Std.Error DF t-value p-value
#(Intercept) 0.3906798322 0.0640391495 24 6.1006405 2.661703e-06
#SpeciesB -0.0303078937 0.0777180616 24 -0.3899723 6.999965e-01
#time -0.0016541839 0.0003059863 24 -5.4060727 1.491893e-05
#SpeciesB:time 0.0002578782 0.0004048368 24 0.6369930 5.301592e-01
Ни точки пересечения, ни склоны существенно не отличаются. Теперь давайте попробуем ANOVA.
anova(fit2)
numDF denDF F-value p-value
(Intercept) 1 24 9.0061 0.0062
Species 1 24 525.7457 <.0001
time 1 24 56.5135 <.0001
Species:time 1 24 0.4058 0.5302
Для сравнения без дисперсионной структуры:
anova(fit1)
numDF denDF F-value p-value
(Intercept) 1 24 29.536428 <.0001
Species 1 24 0.319802 0.5770
time 1 24 17.602173 0.0003
Species:time 1 24 0.041482 0.8403
Таким образом, вы получаете ту же проблему с моделью, которая использует четыре параметра меньше. И теперь я не знаю, почему эффект вида значим в последовательном ANOVA, если включена структура дисперсии, хотя соответствующий параметр модели не имеет значения. Вы можете изучить Pinheiro & Bates 2000 и попытаться найти себя или спросить о Cross Validated.