Что быстрее, поиск по хэшу или бинарный поиск?
Когда дан статический набор объектов (статический в том смысле, что когда-то он загружается, он редко, если вообще меняется), в который требуется повторный параллельный поиск с оптимальной производительностью, что лучше, HashMap или массив с бинарным поиском, используя какой-то пользовательский компаратор?
Является ли ответ функцией типа объекта или структуры? Хэш и / или Равная производительность функции? Уникальность хеша? Размер списка? Hashset размер / установить размер?
Размер набора, который я рассматриваю, может быть от 500 до 10 метров - в случае, если эта информация полезна.
Пока я ищу ответ на C#, я думаю, что истинный математический ответ не в языке, поэтому я не включаю этот тег. Однако, если есть какие-то специфичные для C# вещи, о которых нужно знать, эта информация желательна.
16 ответов
Хорошо, я постараюсь быть коротким.
C# краткий ответ:
Проверьте два разных подхода.
.NET предоставляет вам инструменты для изменения вашего подхода с помощью строки кода. В противном случае используйте System.Collections.Generic.Dictionary и обязательно инициализируйте его с большим числом в качестве начальной емкости, иначе вы передадите остаток своей жизни, вставляя элементы из-за работы, которую GC должен выполнить для сбора старых массивов сегментов.
Более длинный ответ:
Хеш-таблица имеет ПОСЛЕДНЕЕ постоянное время поиска, и получение элемента в хеш-таблице в реальном мире не просто требует вычисления хеша.
Чтобы получить элемент, ваша хеш-таблица будет делать что-то вроде этого:
- Получить хэш ключа
- Получить номер корзины для этого хэша (обычно функция карты выглядит следующим образом: bucket = hash% bucketsCount)
- Пройдите по цепочке элементов (в основном это список элементов, которые используют один и тот же сегмент, большинство хеш-таблиц используют этот метод обработки столкновений блоков / хэшей), который начинается с этого сегмента и сравнивает каждый ключ с элементом, который вы пытаетесь добавить / удалить / обновить / проверить, если содержится.
Время поиска зависит от того, насколько "хорош" (насколько редок результат) и насколько быстро ваша хеш-функция, количество сегментов, которые вы используете, и скорость сравнения ключей, это не всегда лучшее решение.
Лучшее и более глубокое объяснение: http://en.wikipedia.org/wiki/Hash_table
Для очень маленьких коллекций разница будет незначительной. В нижней части вашего диапазона (500 тыс. Предметов) вы начнете видеть разницу, если вы делаете много поисков. Двоичный поиск будет O(log n), тогда как поиск по хешу будет O(1), амортизированный. Это не то же самое, что действительно константа, но вам все равно придется иметь довольно ужасную хеш-функцию, чтобы получить худшую производительность, чем бинарный поиск.
(Когда я говорю "ужасный хэш", я имею в виду что-то вроде:
hashCode()
{
return 0;
}
Да, он сам по себе очень быстрый, но превращает вашу хэш-карту в связанный список.)
ialiashkevich написал некоторый код C#, используя массив и словарь для сравнения двух методов, но он использовал длинные значения для ключей. Я хотел протестировать что-то, что фактически выполняло бы хеш-функцию во время поиска, поэтому я изменил этот код. Я изменил его, чтобы использовать значения String, и я реорганизовал разделы заполнения и поиска в свои собственные методы, чтобы их было легче увидеть в профилировщике. Я также оставил в коде, который использовал значения Long, просто для сравнения. Наконец, я избавился от пользовательской функции двоичного поиска и использовал ее в Array учебный класс.
Вот этот код:
class Program
{
private const long capacity = 10_000_000;
private static void Main(string[] args)
{
testLongValues();
Console.WriteLine();
testStringValues();
Console.ReadLine();
}
private static void testStringValues()
{
Dictionary<String, String> dict = new Dictionary<String, String>();
String[] arr = new String[capacity];
Stopwatch stopwatch = new Stopwatch();
Console.WriteLine("" + capacity + " String values...");
stopwatch.Start();
populateStringArray(arr);
stopwatch.Stop();
Console.WriteLine("Populate String Array: " + stopwatch.ElapsedMilliseconds);
stopwatch.Reset();
stopwatch.Start();
populateStringDictionary(dict, arr);
stopwatch.Stop();
Console.WriteLine("Populate String Dictionary: " + stopwatch.ElapsedMilliseconds);
stopwatch.Reset();
stopwatch.Start();
Array.Sort(arr);
stopwatch.Stop();
Console.WriteLine("Sort String Array: " + stopwatch.ElapsedMilliseconds);
stopwatch.Reset();
stopwatch.Start();
searchStringDictionary(dict, arr);
stopwatch.Stop();
Console.WriteLine("Search String Dictionary: " + stopwatch.ElapsedMilliseconds);
stopwatch.Reset();
stopwatch.Start();
searchStringArray(arr);
stopwatch.Stop();
Console.WriteLine("Search String Array: " + stopwatch.ElapsedMilliseconds);
}
/* Populate an array with random values. */
private static void populateStringArray(String[] arr)
{
for (long i = 0; i < capacity; i++)
{
arr[i] = generateRandomString(20) + i; // concatenate i to guarantee uniqueness
}
}
/* Populate a dictionary with values from an array. */
private static void populateStringDictionary(Dictionary<String, String> dict, String[] arr)
{
for (long i = 0; i < capacity; i++)
{
dict.Add(arr[i], arr[i]);
}
}
/* Search a Dictionary for each value in an array. */
private static void searchStringDictionary(Dictionary<String, String> dict, String[] arr)
{
for (long i = 0; i < capacity; i++)
{
String value = dict[arr[i]];
}
}
/* Do a binary search for each value in an array. */
private static void searchStringArray(String[] arr)
{
for (long i = 0; i < capacity; i++)
{
int index = Array.BinarySearch(arr, arr[i]);
}
}
private static void testLongValues()
{
Dictionary<long, long> dict = new Dictionary<long, long>(Int16.MaxValue);
long[] arr = new long[capacity];
Stopwatch stopwatch = new Stopwatch();
Console.WriteLine("" + capacity + " Long values...");
stopwatch.Start();
populateLongDictionary(dict);
stopwatch.Stop();
Console.WriteLine("Populate Long Dictionary: " + stopwatch.ElapsedMilliseconds);
stopwatch.Reset();
stopwatch.Start();
populateLongArray(arr);
stopwatch.Stop();
Console.WriteLine("Populate Long Array: " + stopwatch.ElapsedMilliseconds);
stopwatch.Reset();
stopwatch.Start();
searchLongDictionary(dict);
stopwatch.Stop();
Console.WriteLine("Search Long Dictionary: " + stopwatch.ElapsedMilliseconds);
stopwatch.Reset();
stopwatch.Start();
searchLongArray(arr);
stopwatch.Stop();
Console.WriteLine("Search Long Array: " + stopwatch.ElapsedMilliseconds);
}
/* Populate an array with long values. */
private static void populateLongArray(long[] arr)
{
for (long i = 0; i < capacity; i++)
{
arr[i] = i;
}
}
/* Populate a dictionary with long key/value pairs. */
private static void populateLongDictionary(Dictionary<long, long> dict)
{
for (long i = 0; i < capacity; i++)
{
dict.Add(i, i);
}
}
/* Search a Dictionary for each value in a range. */
private static void searchLongDictionary(Dictionary<long, long> dict)
{
for (long i = 0; i < capacity; i++)
{
long value = dict[i];
}
}
/* Do a binary search for each value in an array. */
private static void searchLongArray(long[] arr)
{
for (long i = 0; i < capacity; i++)
{
int index = Array.BinarySearch(arr, arr[i]);
}
}
/**
* Generate a random string of a given length.
* Implementation from https://stackru.com/a/1344258/1288
*/
private static String generateRandomString(int length)
{
var chars = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789";
var stringChars = new char[length];
var random = new Random();
for (int i = 0; i < stringChars.Length; i++)
{
stringChars[i] = chars[random.Next(chars.Length)];
}
return new String(stringChars);
}
}
Вот результаты с несколькими различными размерами коллекций. (Время в миллисекундах.)
500000 длинных значений...
Заполните длинный словарь: 26
Заполните длинный массив: 2
Поиск длинного словаря: 9
Поиск длинного массива: 80500000 строковых значений...
Заполнить строковый массив: 1237
Заполните словарь строк: 46
Сортировать массив строк: 1755
Поиск строки словарь: 27
Поисковый массив: 15691000000 длинных значений...
Заполните длинный словарь: 58
Заполните длинный массив: 5
Поиск по длинному словарю: 23
Поиск длинного массива: 1361000000 строковых значений...
Заполните массив строк: 2070
Заполните словарь строк: 121
Сортировать массив строк: 3579
Поиск строки словарь: 58
Поисковый массив: 32673000000 Длинные значения...
Заполните длинный словарь: 207
Заполните длинный массив: 14
Поиск по длинному словарю: 75
Поиск длинного массива: 4353000000 строковых значений...
Заполнить строковый массив: 5553
Заполните словарь строк: 449
Сортировать массив строк: 11695
Поиск строки словарь: 194
Поисковый массив: 1059410000000 длинных значений...
Заполните длинный словарь: 521
Заполните длинный массив: 47
Поиск по длинному словарю: 202
Поиск длинного массива: 118110000000 строковых значений...
Заполнить массив строк: 18119
Заполните словарь строк: 1088
Сортировать массив строк: 28174
Поиск строки словарь: 747
Массив строк поиска: 26503
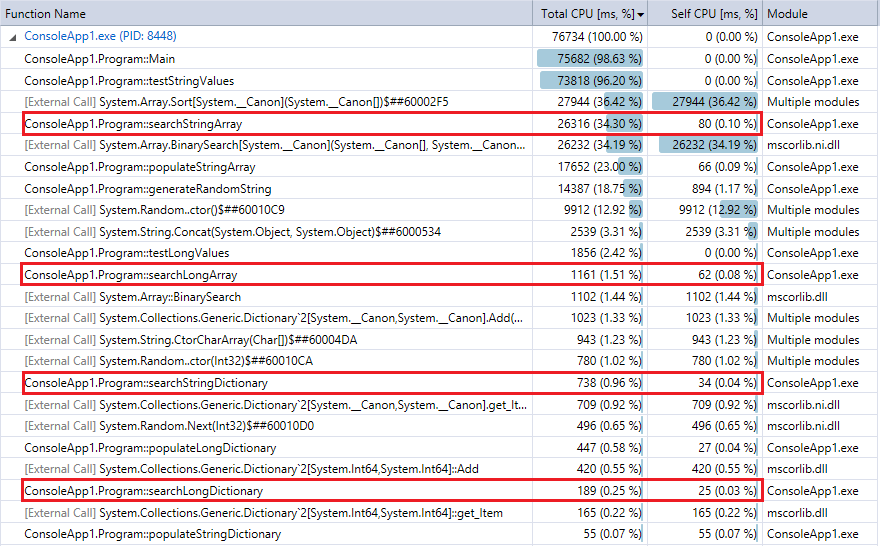
И для сравнения, вот вывод профилировщика для последнего запуска программы (10 миллионов записей и поисков). Я выделил соответствующие функции. Они довольно близко согласуются с метриками хронометража секундомера выше.
Вы можете видеть, что поиск по словарю выполняется намного быстрее, чем бинарный поиск, и (как и ожидалось) разница тем сильнее, чем больше коллекция. Таким образом, если у вас есть разумная функция хеширования (довольно быстрая, с небольшим количеством коллизий), поиск хеша должен превзойти двоичный поиск коллекций в этом диапазоне.
Ответы Бобби, Билла и Корбина неверны. O(1) не медленнее, чем O(log n) для фиксированного / ограниченного n:
log (n) является постоянным, поэтому оно зависит от постоянного времени.
А для медленной хэш-функции, когда-нибудь слышали о md5?
Алгоритм хеширования строк по умолчанию, вероятно, затрагивает все символы и может быть в 100 раз медленнее, чем среднее сравнение для длинных строковых ключей. Был там, сделал это.
Вы можете быть в состоянии (частично) использовать основание. Если вы можете разделить на 256 блоков примерно одинакового размера, вы ищете бинарный поиск от 2k до 40k. Это может обеспечить гораздо лучшую производительность.
[Редактировать] Слишком много людей голосуют за то, что они не понимают.
Строковые сравнения для бинарного поиска отсортированных наборов имеют очень интересное свойство: они становятся медленнее, чем ближе к цели. Сначала они сломаются на первом символе, в конце только на последнем. Предполагать, что постоянное время для них неверно.
Единственный разумный ответ на этот вопрос: это зависит. Это зависит от размера ваших данных, формы ваших данных, вашей реализации хеш-функции, вашей реализации двоичного поиска и того, где живут ваши данные (даже если это не упоминается в вопросе). Несколько других ответов говорят так же, так что я могу просто удалить это. Тем не менее, было бы неплохо поделиться тем, что я узнал из обратной связи с моим первоначальным ответом.
- Я написал: "Алгоритмы хеширования - это O(1), а бинарный поиск - это O(log n)". Как отмечалось в комментариях, система обозначений Big O оценивает сложность, а не скорость. Это абсолютно верно. Стоит отметить, что мы обычно используем сложность, чтобы понять требования алгоритма к времени и пространству. Таким образом, хотя глупо полагать, что сложность строго совпадает со скоростью, оценка сложности без времени и пространства в глубине вашего ума является необычной. Моя рекомендация: избегайте обозначений Big O
- Я написал: "Так как n приближается к бесконечности..." - это самая глупая вещь, которую я мог бы включить в ответ. Бесконечность не имеет ничего общего с вашей проблемой. Вы упоминаете верхнюю границу в 10 миллионов. Игнорировать бесконечность. Как отмечают комментаторы, очень большие числа будут создавать всевозможные проблемы с хэшем. (Очень большие числа не делают бинарный поиск прогулкой по парку.) Моя рекомендация: не упоминайте бесконечность, если вы не имеете в виду бесконечность.
- Также из комментариев: остерегайтесь строковых хэшей по умолчанию (Вы хешируете строки? Вы не упоминаете.), Индексы базы данных часто являются b-деревьями (пища для размышлений). Моя рекомендация: рассмотрите все ваши варианты. Рассмотрим другие структуры данных и подходы... как старомодный три (для хранения и извлечения строк) или R-дерево (для пространственных данных) или MA-FSA (минимальный ациклический конечный автомат - небольшой объем памяти).
Учитывая комментарии, вы можете предположить, что люди, которые используют хеш-таблицы, являются ненормальными. Хеш-таблицы безрассудны и опасны? Эти люди безумны?
Оказывается, они не. Подобно тому, как двоичные деревья хороши в определенных вещах (обход данных по порядку, эффективность хранения), у хэш-таблиц тоже есть свой момент. В частности, они могут быть очень хороши при сокращении количества операций чтения, необходимых для получения ваших данных. Алгоритм хеширования может генерировать местоположение и переходить прямо к нему в памяти или на диске, в то время как бинарный поиск считывает данные во время каждого сравнения, чтобы решить, что читать дальше. Каждое чтение может привести к потере кэша, которая на порядок (или более) медленнее, чем инструкция процессора.
Это не значит, что хеш-таблицы лучше, чем бинарный поиск. Они не. Также нельзя утверждать, что все реализации хеширования и двоичного поиска одинаковы. Они не. Если у меня есть точка зрения, это так: оба подхода существуют по причине. Вам решать, что лучше для ваших нужд.
Оригинальный ответ:
Хеш-алгоритмы O(1), а бинарный поиск O(log n). Таким образом, по мере приближения n к бесконечности производительность хэша улучшается относительно бинарного поиска. Ваш пробег будет варьироваться в зависимости от n, вашей реализации хеша и вашей реализации бинарного поиска.
Интересная дискуссия по О (1). Перефразировано:
O(1) не означает мгновенный. Это означает, что производительность не меняется с ростом размера n. Вы можете разработать алгоритм хеширования, который будет настолько медленным, что никто бы его не использовал, и он все равно будет O(1). Я вполне уверен, что.NET/C# не страдает от чрезмерно дорогого хэширования;)
Хэши, как правило, быстрее, хотя бинарный поиск имеет лучшие характеристики в худшем случае. Доступ к хешу обычно является вычислением, чтобы получить значение хеша, чтобы определить, в каком "сегменте" будет запись, и, таким образом, производительность, как правило, будет зависеть от того, насколько равномерно распределены записи, и от метода, используемого для поиска в сегменте. Плохая хеш-функция (оставляя несколько сегментов с большим количеством записей) с линейным поиском по сегментам приведет к медленному поиску. (С третьей стороны, если вы читаете диск, а не память, хэш-блоки, вероятно, будут смежными, в то время как двоичное дерево в значительной степени гарантирует нелокальный доступ.)
Если вы хотите вообще быстро, используйте хеш. Если вы действительно хотите гарантированно ограниченную производительность, вы можете использовать двоичное дерево.
Если ваш набор объектов действительно статичен и неизменен, вы можете использовать идеальный хеш, чтобы получить гарантированную производительность O(1). Я видел упомянутое несколько раз о gperf, хотя мне никогда не приходилось использовать его самому.
Dictionary/Hashtable использует больше памяти и занимает больше времени для сравнения по сравнению с массивом. Но поиск выполняется быстрее с помощью словаря, а не бинарный поиск в массиве.
Вот числа для 10 миллионов элементов Int64 для поиска и заполнения. Плюс пример кода, который вы можете запустить самостоятельно.
Словарь памяти: 462 836
Память массива: 88 376
Заполнить словарь: 402
Заполнить массив: 23
Поиск в словаре: 176
Поисковый массив: 680
using System;
using System.Collections.Generic;
using System.Diagnostics;
namespace BinaryVsDictionary
{
internal class Program
{
private const long Capacity = 10000000;
private static readonly Dictionary<long, long> Dict = new Dictionary<long, long>(Int16.MaxValue);
private static readonly long[] Arr = new long[Capacity];
private static void Main(string[] args)
{
Stopwatch stopwatch = new Stopwatch();
stopwatch.Start();
for (long i = 0; i < Capacity; i++)
{
Dict.Add(i, i);
}
stopwatch.Stop();
Console.WriteLine("Populate Dictionary: " + stopwatch.ElapsedMilliseconds);
stopwatch.Reset();
stopwatch.Start();
for (long i = 0; i < Capacity; i++)
{
Arr[i] = i;
}
stopwatch.Stop();
Console.WriteLine("Populate Array: " + stopwatch.ElapsedMilliseconds);
stopwatch.Reset();
stopwatch.Start();
for (long i = 0; i < Capacity; i++)
{
long value = Dict[i];
// Console.WriteLine(value + " : " + RandomNumbers[i]);
}
stopwatch.Stop();
Console.WriteLine("Search Dictionary: " + stopwatch.ElapsedMilliseconds);
stopwatch.Reset();
stopwatch.Start();
for (long i = 0; i < Capacity; i++)
{
long value = BinarySearch(Arr, 0, Capacity, i);
// Console.WriteLine(value + " : " + RandomNumbers[i]);
}
stopwatch.Stop();
Console.WriteLine("Search Array: " + stopwatch.ElapsedMilliseconds);
Console.ReadLine();
}
private static long BinarySearch(long[] arr, long low, long hi, long value)
{
while (low <= hi)
{
long median = low + ((hi - low) >> 1);
if (arr[median] == value)
{
return median;
}
if (arr[median] < value)
{
low = median + 1;
}
else
{
hi = median - 1;
}
}
return ~low;
}
}
}
Удивительно, что никто не упомянул хеширование Cuckoo, которое обеспечивает гарантированный O(1) и, в отличие от идеального хеширования, способно использовать всю выделяемую память, в то время как идеальное хеширование может закончиться гарантированным O(1), но тратит большую часть его распределение. Предостережение? Время вставки может быть очень медленным, особенно с увеличением количества элементов, поскольку вся оптимизация выполняется на этапе вставки.
Я полагаю, что некоторая версия этого используется в аппаратном обеспечении маршрутизатора для поиска IP.
См текст ссылки
Я сильно подозреваю, что в проблемном наборе размером ~1M хеширование будет быстрее.
Просто по номерам:
бинарный поиск потребует ~ 20 сравнений (2^20 == 1M)
поиск хеша потребует 1 вычисления хеша для ключа поиска и, возможно, несколько сравнений впоследствии для устранения возможных коллизий
Изменить: номера:
for (int i = 0; i < 1000 * 1000; i++) {
c.GetHashCode();
}
for (int i = 0; i < 1000 * 1000; i++) {
for (int j = 0; j < 20; j++)
c.CompareTo(d);
}
времена: c = "abcde", d = "rwerij" хэш-код: 0,0012 секунды. Сравните: 2,4 секунды.
Отказ от ответственности: На самом деле сравнительный анализ хеш-поиска по сравнению с бинарным может быть лучше, чем этот не совсем релевантный тест. Я даже не уверен, что GetHashCode запоминается под капотом
Интересно, почему никто не упомянул идеальное хеширование.
Это актуально только в том случае, если ваш набор данных зафиксирован в течение длительного времени, но для этого он анализирует данные и создает идеальную хеш-функцию, которая гарантирует отсутствие коллизий.
Довольно аккуратно, если ваш набор данных постоянен и время для вычисления функции мало по сравнению со временем выполнения приложения.
Я бы сказал, что это зависит главным образом от производительности методов хеширования и сравнения. Например, при использовании строковых ключей, которые очень длинные, но случайные, сравнение всегда даст очень быстрый результат, но хеш-функция по умолчанию обработает всю строку.
Но в большинстве случаев хэш-карта должна быть быстрее.
Этот вопрос является более сложным, чем объем чисто алгоритмической производительности. Если мы уберем факторы, что алгоритм бинарного поиска более дружественен к кешу, поиск хеша в общем смысле будет быстрее. Лучший способ выяснить это - построить программу и отключить опции оптимизации компилятора, и мы могли бы обнаружить, что поиск хеш-функции быстрее, учитывая его эффективность по времени алгоритма O(1) в общем смысле.
Но когда вы включаете оптимизацию компилятора и пробуете тот же тест с меньшим числом выборок, скажем, менее 10 000, бинарный поиск превзошел поиск по хешу, используя преимущества своей структуры данных, удобной для кэша.
Это скорее комментарий к ответу Билла, потому что в его ответе так много откликов, хотя он и неправильный. Поэтому я должен был опубликовать это.
Я вижу много дискуссий о том, какова сложность поиска в хеш-таблице наихудшего случая, и что считается амортизированным анализом / что нет. Пожалуйста, проверьте ссылку ниже
Сложность выполнения хеш-таблицы (вставка, поиск и удаление)
в худшем случае сложность O(n), а не O(1), в отличие от того, что говорит Билл. И, следовательно, его сложность O(1) не амортизируется, так как этот анализ может использоваться только для наихудших случаев (так говорит и его собственная ссылка в Википедии)
Это зависит от того, как вы обрабатываете дубликаты для хеш-таблиц (если вообще). Если вы хотите разрешить дублирование хеш-ключа (без хеш-функции, идеально), остается поиск O(1) для поиска первичного ключа, но поиск "правильного" значения может быть дорогостоящим. Ответ, теоретически, в большинстве случаев, хэши быстрее. YMMV в зависимости от того, какие данные вы положили туда...
Здесь описывается, как создаются хэши, и поскольку универсум ключей достаточно большой, а хэш-функции построены так, чтобы быть "очень инъективными", так что коллизии редко случаются, время доступа к хеш-таблице на самом деле не O(1)... это что-то на основе некоторых вероятностей. Но разумно сказать, что время доступа к хешу почти всегда меньше времени O(log_2(n))
Ответ зависит. Давайте подумаем, что количество элементов n очень велико. Если вы хороши в написании лучшей хеш-функции, которая меньше коллизий, то хеширование является лучшим.Обратите внимание, что хеш-функция выполняется только один раз при поиске и направляется в соответствующий сегмент. Так что это не большие накладные расходы, если n велико.
Проблема в Hashtable: Но проблема в хеш-таблицах заключается в том, что если хеш-функция не годится (происходит больше коллизий), тогда поиск не O(1). Он стремится к O(n), потому что поиск в сегменте - это линейный поиск. Может быть хуже, чем двоичное дерево. проблема в двоичном дереве: в двоичном дереве, если дерево не сбалансировано, оно также стремится к O(n). Например, если вы вставили 1,2,3,4,5 в двоичное дерево, это был бы скорее список. Итак, если вы видите хорошую методологию хеширования, используйте хеш-таблицу. Если нет, лучше использовать двоичное дерево.
Конечно, хеш является самым быстрым для такого большого набора данных.
Еще один способ ускорить его, поскольку данные редко изменяются, - это программно сгенерировать специальный код для выполнения первого уровня поиска в виде гигантского оператора switch (если ваш компилятор может его обработать), а затем перейти к поиску полученное ведро.