Использование сглаживания в ggplot2 для подбора линейной модели с использованием ошибок, приведенных в данных

У меня есть этот фрейм данных:

> dat
   x         y        yerr
1 -1 -1.132711 0.001744498
2 -2 -2.119657 0.003889120
3 -3 -3.147378 0.007521881
4 -4 -4.220129 0.012921450
5 -5 -4.586586 0.021335644
6 -6 -5.389198 0.032892630
7 -7 -6.002848 0.048230946

И я могу построить это со стандартным сглаживанием ошибок как:

p <- ggplot(dat, aes(x=x, y=y)) + geom_point()
p <- p + geom_errorbar(data=dat, aes(x=x, ymin=y-yerr, ymax=y+yerr), width=0.09)
p + geom_smooth(method = "lm", formula = y ~ x)

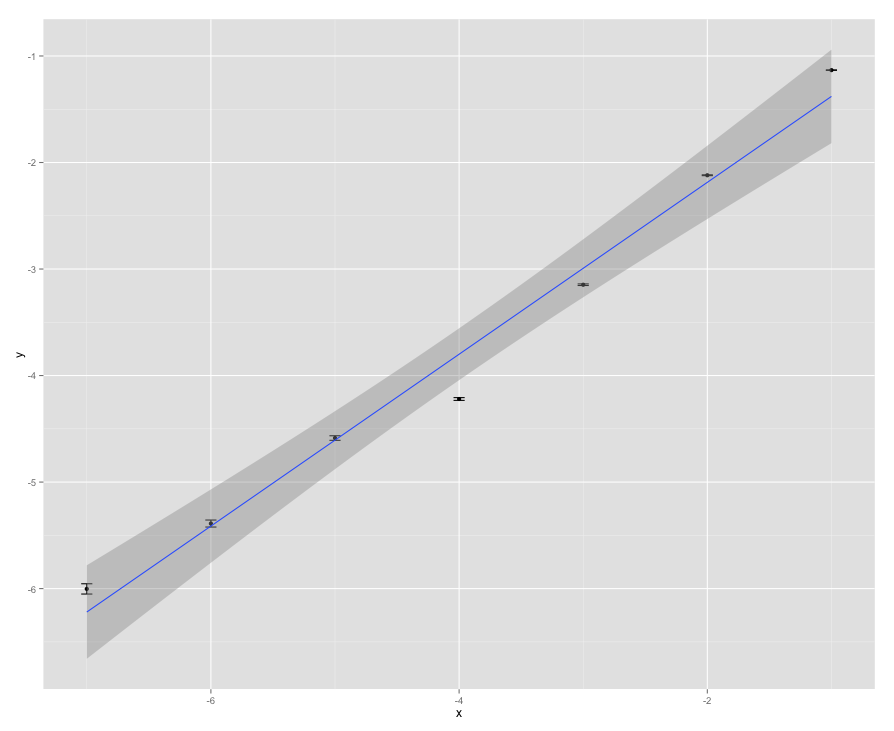
Но мне нужно использовать yerr, чтобы соответствовать моей линейной модели. Это возможно с ggplot2?

Источник

3 ответа

Решение

Ну, я нашел способ ответить на это.

Поскольку в любом научном эксперименте, где мы собираем данные, если этот эксперимент выполнен правильно, все значения данных должны иметь связанную с этим ошибку.

В некоторых случаях дисперсия ошибки может быть одинаковой во всех точках, но во многих, как в настоящем случае говорится в первоначальном вопросе, это не так. Поэтому мы должны использовать это различие в дисперсиях значений ошибок для разных измерений при подборе кривой к нашим данным.

Этот способ сделать это - приписать вес значениям ошибки, которые согласно методам статистического анализа равны 1/sqrt(errorValue), поэтому он становится:

p <- ggplot(dat, aes(x=x, y=y, weight = 1/sqrt(yerr))) + 
    geom_point() + 
    geom_errorbar(aes(ymin=y-yerr, ymax=y+yerr), width=0.09) + 
    geom_smooth(method = "lm", formula = y ~ x)

введите описание изображения здесь

Источник

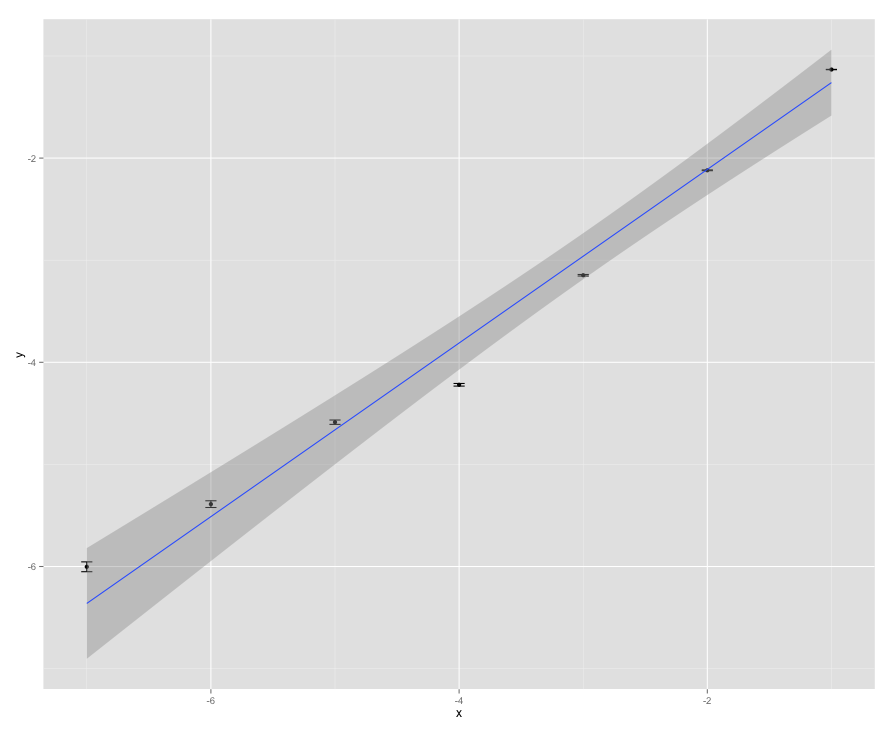
Для подгонки любой модели я бы делал примерку вне используемой мной парадигмы построения. Для этого передайте значение weights это обратно пропорционально дисперсиям наблюдений. Подгонка будет производиться с помощью процедуры взвешенных наименьших квадратов.

Для вашего примера / ситуации ggplot's geom_smooth делает следующее для вас. Виста может показаться проще в использовании geom_SmoothПреимущества подгонки модели напрямую со временем перевешивают это. Например, у вас есть подходящая модель и вы можете выполнить диагностику соответствия, предположений модели и т. Д.

Установите взвешенные наименьшие квадраты

mod <- lm(y ~ x, data = dat, weights = 1/sqrt(yerr))

затем predict() от модели в диапазоне x

newx <- with(dat, data.frame(x = seq(min(x), max(x), length = 50)))
pred <- predict(mod, newx, interval = "confidence", level = 0.95)

Выше мы получаем predict.lm метод для создания соответствующего доверительного интервала для использования.

Далее подготовим данные для построения

pdat <- with(data.frame(pred),
             data.frame(x = newx, y = fit, ymax = upr, ymin = lwr))

Далее строим сюжет

require(ggplot2)
p <- ggplot(dat, aes(x = x, y = y)) +
       geom_point() +
       geom_line(data = pdat, colour = "blue") + 
       geom_ribbon(mapping = aes(ymax = ymax, ymin = ymin), data = pdat, 
                   alpha = 0.4, fill = "grey60")
p
Источник

Ваш вопрос немного расплывчатый. Вот пара предложений, которые могут помочь вам начать.

  1. ggplot2 просто использует lm функция регрессии. Чтобы получить значения, просто выполните:

     lm(y ~ x, data=dat)

    это даст вам y-перехват и градиент.

  2. Вы можете отключить стандартную ошибку в stat_smooth с использованием se аргумент:

    .... + geom_smooth(method = "lm", formula = y ~ x, se = FALSE)

  3. Вы можете добавить ленту через ваши точки / полосы ошибок с помощью:

    ##This doesn't look good. 
.... + geom_ribbon(aes(x=x, ymax =y+yerr, ymin=y-yerr))
Источник
Другие вопросы по тегам