Заменить цепочку размытия изображения одним размытием
В этом вопросе я спросил, как реализовать цепочку размытий за один шаг.
Затем я узнал из гауссовой размытой страницы Википедии, что:
Применение нескольких последовательных размытий по Гауссу к изображению имеет тот же эффект, что и применение одного большего размытия по Гауссу, радиус которого является корнем квадратным из суммы квадратов радиусов размытия, которые были фактически применены. Например, применение последовательных размытий по Гауссу с радиусами 6 и 8 дает те же результаты, что и применение одного размытия по Гауссу с радиусом 10, так как sqrt {6^{2}+8^{2}}=10.
Так что я подумал, что blur а также singleBlur были одинаковыми в следующем коде:
cv::Mat firstLevel;
float sigma1, sigma2;
//intialize firstLevel, sigma1 and sigma2
cv::Mat blur = gaussianBlur(firstLevel, sigma1);
blur = gaussianBlur(blur, sigma2);
float singleSigma = std::sqrt(std::pow(sigma1,2)+std::pow(sigma2,2));
cv::Mat singleBlur = gaussianBlur(firstLevel, singleSigma);
cv::Mat diff = blur != singleBLur;
// Equal if no elements disagree
assert( cv::countNonZero(diff) == 0);
Но это assert не удается (и на самом деле, например, первый ряд blur отличается от первого из singleBlur).
Зачем?
ОБНОВИТЬ:
После разных комментариев, запрашивающих дополнительную информацию, я обновлю ответ.
Я пытаюсь распараллелить этот код. В частности, я сосредоточен сейчас на вычислении всех пятен на всех уровнях заранее. Серийный код (который работает правильно) следующий:
vector<Mat> blurs ((par.numberOfScales+3)*levels, Mat());
cv::Mat octaveLayer = firstLevel;
int scaleCycles = par.numberOfScales+2;
//compute blurs at all layers (not parallelizable)
for(int i=0; i<levels; i++){
blurs[i*scaleCycles+1] = octaveLayer.clone();
for (int j = 1; j < scaleCycles; j++){
float sigma = par.sigmas[j]* sqrt(sigmaStep * sigmaStep - 1.0f);
blurs[j+1+i*scaleCycles] = gaussianBlur(blurs[j+i*scaleCycles], sigma);
if(j == par.numberOfScales)
octaveLayer = halfImage(blurs[j+1+i*scaleCycles]);
}
}
Куда:
Mat halfImage(const Mat &input)
{
Mat n(input.rows/2, input.cols/2, input.type());
float *out = n.ptr<float>(0);
for (int r = 0, ri = 0; r < n.rows; r++, ri += 2)
for (int c = 0, ci = 0; c < n.cols; c++, ci += 2)
*out++ = input.at<float>(ri,ci);
return n;
}
Mat gaussianBlur(const Mat input, const float sigma)
{
Mat ret(input.rows, input.cols, input.type());
int size = (int)(2.0 * 3.0 * sigma + 1.0); if (size % 2 == 0) size++;
GaussianBlur(input, ret, Size(size, size), sigma, sigma, BORDER_REPLICATE);
return ret;
}
Я извиняюсь за ужасные индексы выше, но я пытался уважать оригинальную систему кода (что ужасно, как начать считать с 1 вместо 0). Код выше имеет scaleCycles=5 а также levels=6 Таким образом, в общей сложности 30 пятен.
Это версия "одиночного размытия", где сначала я вычисляю сигмы для каждого размытия, которое должно быть вычислено (следуя формуле Википедии), а затем применяю размытие (обратите внимание, что оно все еще последовательное и не распараллеливается):
vector<Mat> singleBlurs ((par.numberOfScales+3)*levels, Mat());
vector<float> singleSigmas(scaleCycles);
float acc = 0;
for (int j = 1; j < scaleCycles; j++){
float sigma = par.sigmas[j]* sqrt(sigmaStep * sigmaStep - 1.0f);
acc += pow(sigma, 2);
singleSigmas[j] = sqrt(acc);
}
octaveLayer = firstLevel;
for(int i=0; i<levels; i++){
singleBlurs[i*scaleCycles+1] = octaveLayer.clone();
for (int j = 1; j < scaleCycles; j++){
float sigma = singleSigmas[j];
std::cout<<"j="<<j<<" sigma="<<sigma<<std::endl;
singleBlurs[j+1+i*scaleCycles] = gaussianBlur(singleBlurs[j+i*scaleCycles], sigma);
if(j == par.numberOfScales)
octaveLayer = halfImage(singleBlurs[j+1+i*scaleCycles]);
}
}
Конечно, код выше генерирует 30 пятен также с такими же параметрами предыдущей версии.
И тогда это код, чтобы увидеть разницу между каждым signgleBlurs а также blurs:
assert(blurs.size() == singleBlurs.size());
vector<Mat> blurDiffs(blurs.size());
for(int i=1; i<levels*scaleCycles; i++){
cv::Mat diff;
absdiff(blurs[i], singleBlurs[i], diff);
std::cout<<"i="<<i<<"diff rows="<<diff.rows<<" cols="<<diff.cols<<std::endl;
blurDiffs[i] = diff;
std::cout<<"blurs rows="<<blurs[i].rows<<" cols="<<blurs[i].cols<<std::endl;
std::cout<<"singleBlurs rows="<<singleBlurs[i].rows<<" cols="<<singleBlurs[i].cols<<std::endl;
std::cout<<"blurDiffs rows="<<blurDiffs[i].rows<<" cols="<<blurDiffs[i].cols<<std::endl;
namedWindow( "blueDiffs["+std::to_string(i)+"]", WINDOW_AUTOSIZE );// Create a window for display.
//imshow( "blueDiffs["+std::to_string(i)+"]", blurDiffs[i] ); // Show our image inside it.
//waitKey(0); // Wait for a keystroke in the window
Mat imageF_8UC3;
std::cout<<"converting..."<<std::endl;
blurDiffs[i].convertTo(imageF_8UC3, CV_8U, 255);
std::cout<<"converted"<<std::endl;
imwrite( "blurDiffs_"+std::to_string(i)+".jpg", imageF_8UC3);
}
Теперь, что я видел, это то, что blurDiffs_1.jpg а также blurDiffs_2.jpg черные, но неожиданно от blurDiffs_3.jpg до blurDiffs_29.jpg становится все белее и белее. По какой-то причине blurDiffs_30.jpg почти полностью черный.
Первая (правильная) версия генерирует 1761 дескриптор. Вторая (неправильная) версия генерирует>2.3k дескрипторов.
Я не могу опубликовать blurDiffs Матрицы, потому что (особенно первые) очень большие и пространство поста ограничено. Я выложу несколько образцов. Я не буду отправлять blurDiffs_1.jpg а также blurDiffs_2.jpg потому что они полностью черные. Обратите внимание, что из-за halfImage изображения становятся все меньше и меньше (как и ожидалось).
blurDiffs_3.jpg:
blurDiffs_6.jpg:
blurDiffs_15.jpg:
blurDiffs_29.jpg:
Как изображение читается:
Mat tmp = imread(argv[1]);
Mat image(tmp.rows, tmp.cols, CV_32FC1, Scalar(0));
float *out = image.ptr<float>(0);
unsigned char *in = tmp.ptr<unsigned char>(0);
for (size_t i=tmp.rows*tmp.cols; i > 0; i--)
{
*out = (float(in[0]) + in[1] + in[2])/3.0f;
out++;
in+=3;
}
Кто-то здесь предложил разделить diff к 255, чтобы увидеть реальную разницу, но я не понимаю, почему я правильно его понял.
Если вам нужны подробности, пожалуйста, дайте мне знать.
2 ответа
Предупреждение: у меня нет опыта работы с OpenCV, но следующее относится к вычислению размытия по Гауссу в целом. И это применимо, поскольку я бросил взгляд на документацию OpenCV относительно обработки границ и использования конечных ядер (FIR-фильтрация).
Кроме того: ваш первоначальный тест был чувствителен к округлению, но вы устранили эту проблему и показали, что ошибки намного больше.
Остерегайтесь эффектов границы изображения. Для пикселей около края изображение практически растягивается одним из предложенных способов (
BORDER_DEFAULT, BORDER_REPLICATE,так далее...). Если ваше изображение|abcd|и вы используетеBORDER_REPLICATEВы эффективно фильтруете расширенное изображение aaaa | abcd | dddd. Результатklmn|opqr|stuv, Есть новые значения пикселей(k,l,m,n,s,t,u,v)которые немедленно отбрасываются для получения выходного изображения|opqr|, Если вы теперь примените еще одно размытие по Гауссу, это размытие будет работать на новом расширенном изображенииoooo|opqr|rrrr- отличается от"true"промежуточный результат и, таким образом, дает вам результат, отличный от результата, полученного с помощью одного размытия по Гауссу с большей сигмой.These extension methods are safe though: REFLECT, REFLECT_101, WRAP.Используя конечный размер ядра
G(s1)*G(s2)=G(sqrt(s1^2+s2^2))правило не выполняется вообще из-за обрезания хвостов ядра. Таким образом, вы можете уменьшить ошибку, увеличив размер ядра относительно сигмы, например:int size = (int)(2.0 * 10.0 * sigma + 1.0); if (size % 2 == 0) size++;
Пункт 3, кажется, является проблемой, которая "кусает" вас. Вы действительно заботитесь, G(s1)*G(s2) собственность сохраняется. Оба результата в некотором смысле неверны. Влияет ли это на методологию, которая в основном влияет на результат? Обратите внимание, что пример использования 10x sigma Я дал, может разрешить разницу, но будет намного медленнее.
Обновление: я забыл добавить, что может быть наиболее практичным решением. Вычислить размытие по Гауссу, используя преобразование Фурье. Схема будет такой:
- Вычислить преобразование Фурье (БПФ) вашего входного изображения
- Умножьте с помощью преобразования Фурье ядра Гаусса и вычислите обратное преобразование Фурье. Не обращайте внимания на мнимую часть сложного вывода.
Вы можете найти уравнение для гауссиана в частотной области в Википедии
Вы можете выполнить второй шаг отдельно (т.е. параллельно) для каждой шкалы (сигма). Граничное условие подразумевает вычисление размытия таким образом: BORDER_WRAP, Если вы предпочитаете, вы можете достичь того же, но с BORDER_REFLECT если вы используете дискретное косинусное преобразование (DCT) вместо этого. Не знаю, если OpenCV предоставляет один. Вы будете после DCT-II
Это в основном то, что говорит GM. Помните, что вы не только округляете числа с плавающей точкой, вы также округляете, глядя только на целочисленные точки (как на изображении, так и на ядрах Гаусса).
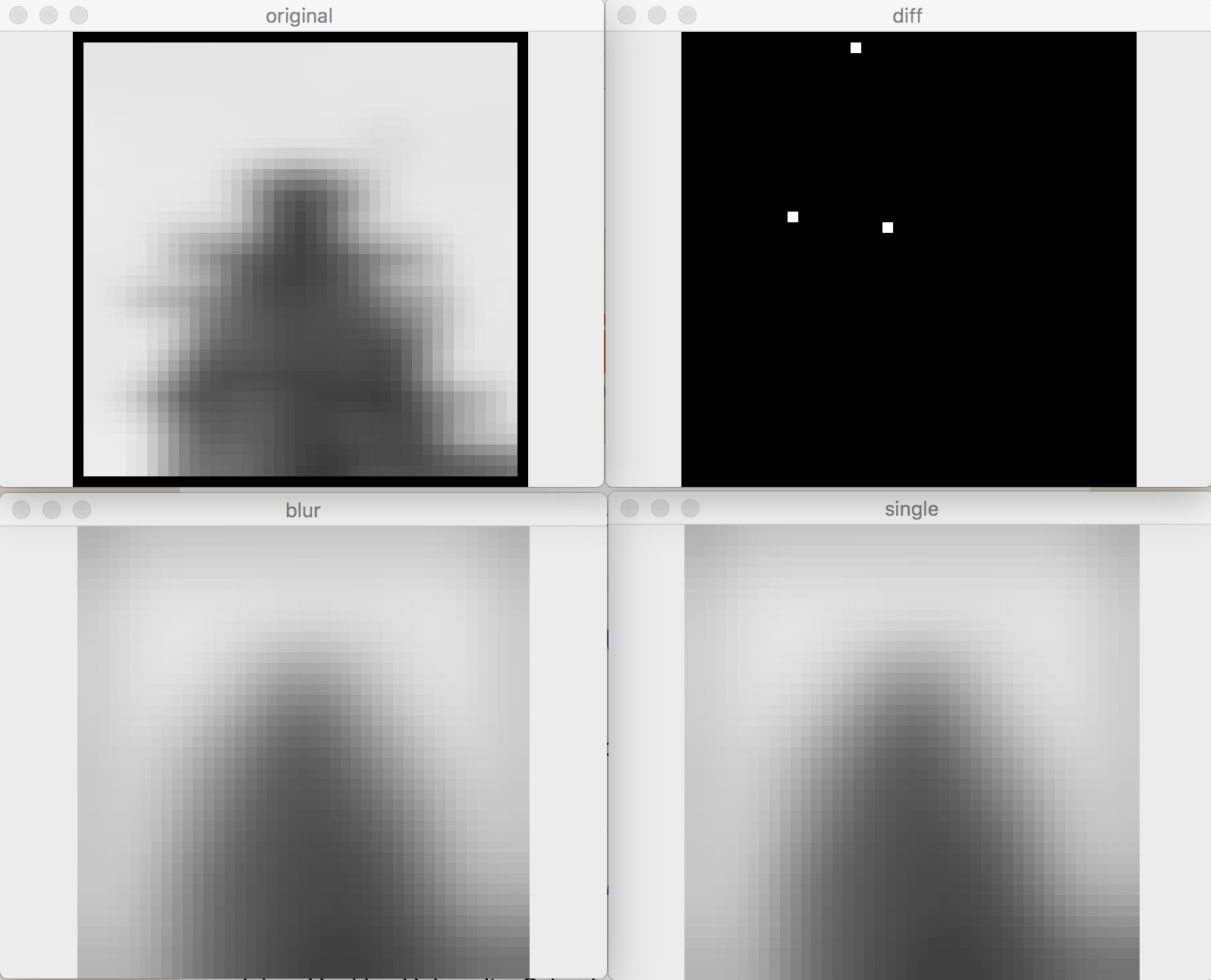
Вот что я получил от маленького (41x41) изображение:
где blur а также single округлены convertTo(...,CV8U) а также diff это где они разные. Таким образом, с точки зрения DSP, это может быть не очень хорошее соглашение. Но в обработке изображений все не так плохо.
Кроме того, я подозреваю, что различие будет менее значительным, так как вы выполняете гауссову для больших изображений.