Matplotlib: Как создать этот элегантный сюжет
Я пытаюсь создать этот сюжет, используя Matplotlib с Python 2.
Ожидаемый результат: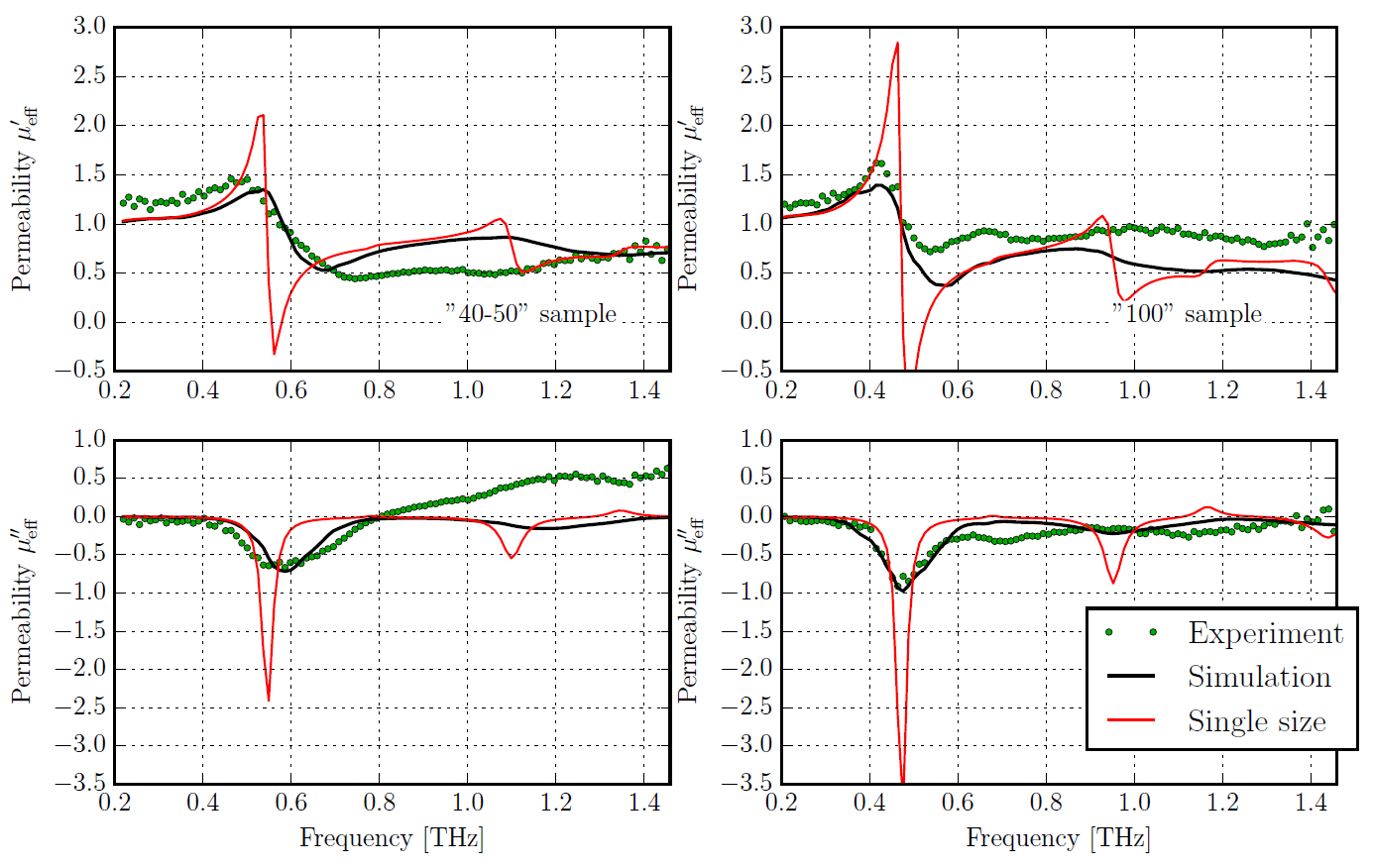
Доступный исходный код выглядит следующим образом.
#!/usr/bin/env python
#-*- coding: utf-8 -*-
from __future__ import division
import matplotlib
import scipy
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt
#import python-mpi todo
## Initialize #{{{
matplotlib.rc('text', usetex=True)
matplotlib.rc('font',**{'family':'serif','serif':['Computer Modern Roman, Times']})
matplotlib.rc('text.latex',unicode=True)
colors = ("#BB3300", "#8800DD", "#2200FF", "#0099DD", "#00AA00", "#AA8800",
"#661100", "#440077", "#000088", "#003366", "#004400", "#554400")
#}}}
## In the measured data (calculated and grouped in PKGraph), the order of properties is:
## x, Nr, Ni, Zr, Zi, eps_r, eps_i, mu_r, mu_i
## 0 1 5 7
## In the Riad's simulation data, the order of properties is:
## x, mu_r, mu_i, eps_r, eps_i, N_r, N_i, Z_r, Z_i
## 0 1 3 5 7
properties = [
#{"name":"Refractive index", "symbol":"$N$", "meas_col":1, "sim_col":5, "ylim":(0., 3.)},
{"name":"Real permeability", "symbol":"Permeability $\\mu_{\\mathrm{eff}}'$", "meas_col":7, "sim_col":1, "ylim":(-.5, 3.)},
{"name":"Imaginary permeability","symbol":"Permeability $\\mu_{\\mathrm{eff}}''$", "meas_col":8, "sim_col":2, "ylim":(-3.5, 1.)},
#{"name":"Permitivitty", "symbol":"$\\varepsilon$", "meas_col":5, "sim_col":3, "ylim":(-1.,6.)},
]
samples_dir = "particle_statistics/"
samples = [
#{"file":"sub38.csv", "name":"sub38", "color":colors[2], "rescaling": 1},
#{"file":"38-40.csv", "name":"38-40", "color":colors[3], "rescaling": 1},
{"file":"40-50.csv", "name":"40-50", "color":colors[4], "rescaling": 15./12},
#{"file":"53.csv", "name":"53", "color":colors[5], "rescaling": 1},
{"file":"100.csv", "name":"100", "color":colors[4], "rescaling": 2, "eps":76.},
]
plt.figure(figsize=(10,6))
for property_ in properties:
for sample in samples:
print property_['name'], sample['name']
print " Load measured spectral data from csv file"#{{{
(meas_x, meas_y) = scipy.loadtxt('measured_spectral_data/N'+sample['file'],
usecols=(0, property_['meas_col']), unpack=True)
#}}}
print " Load simulated spectral data from csv file" #{{{
## Load data
(sim_x, sim_y) = scipy.loadtxt("simulated_spectral_data/d39_ff12_eps92.csv",
usecols=(0, property_['sim_col']), unpack=True)
## Extend the first and last point for proper interpolation out of bounds
sim_x = scipy.append(scipy.array([0]), sim_x)
sim_x = scipy.append(sim_x, scipy.array([max(sim_x)*10]))
sim_y = scipy.append(sim_y[0:1], sim_y)
sim_y = scipy.append(sim_y, sim_y[-2:-1])
## Value used in the Riad Yahiaoui's simulation
sim_particle_size = 39e-6
sim_particle_eps = 94
## Normalize effective size to the mean permittivity of TiO2
## which is eps_o=87, eps_e=165 at frequency of 0,5 THz
## TODO: to be discussed: Correction to possible air voids needed to fit the data!
#meas_particle_eps = (165+87+87)*(1./3) # _ = , theoretical dense TiO2
meas_particle_eps = 94 # suggested in Riad's dis.; this fits well for the '40-50' sample
if sample.has_key('eps'): meas_particle_eps = sample['eps']
#}}}
print " Load particles and calculate histogram of major/minor axis"#{{{
majors, minors = scipy.loadtxt("particle_statistics/"+sample['file'])/1e6 ## the values were stored in micrometers
bins = scipy.arange(2e-6, 140e-6, .1e-6)
bin_particle_count = [0]*(len(bins)-1) # particles_number_in_bin; initialize to zeroes
bin_minor_sum = [0]*(len(bins)-1)
for n in range(len(bins)-1):
for (major, minor) in zip(majors, minors):
if (bins[n]<major) and (major<bins[n+1]):
bin_particle_count[n] += 1
bin_minor_sum[n] += minor
#}}}
print " Sum the response of the particles according to their histogram"#{{{
## Initialize variables
total_response_n = 0*meas_x
total_bins_weight = 0
average_particle_totalsize = 0
average_particle_totalweight = 0
## Scale some properties with respect to those of vacuum instead of zero
vacuum_property = 1. if ("Real" in property_['name']) else 0.
for n in [n for n in range(len(bin_particle_count)) if (bin_particle_count[n]>0)]:
## Properties of this bin
bin_major = (bins[n]+bins[n+1])/2
bin_minor = bin_minor_sum[n]/bin_particle_count[n]
bin_particle_size = (1./3*bin_major**-2 + 1./3*bin_minor**-2 + 1./3*bin_minor**-2)**-.5
## The averaging weight (fill factor) of each bin
# TODO are oblong elipsoids "maj-min-min" correct?
# TODO which power is correct?
filling_factor_power = 2 # XXX
bin_weight_coef = (bin_particle_size/sim_particle_size)**filling_factor_power
bin_weight = bin_particle_count[n] * bin_weight_coef
total_bins_weight += bin_weight
## Calculate response of the bin
scaled_sim_x = sim_x * (sim_particle_size/bin_particle_size) * (sim_particle_eps/meas_particle_eps)
interp_function = interp1d(scaled_sim_x, sim_y, kind='linear', bounds_error=False)
bin_response_n = (interp_function(meas_x) - vacuum_property) * bin_weight
total_response_n += bin_response_n
## Calculate which particle size is the average
average_particle_totalsize += bin_particle_size * bin_weight
average_particle_totalweight += bin_weight
#}}}
print " Get spectrum for average (modus) particle"#{{{
## Prepare data for "clean" unconvolved resonance curve (of average particle size)
#avg_particle_size = average_particle_totalsize / average_particle_totalweight
avg_particle_size = bins[bin_particle_count.index(max(bin_particle_count))]
print " ... ", avg_particle_size
scaled_sim_x = sim_x * (sim_particle_size/avg_particle_size) * (sim_particle_eps/meas_particle_eps)
interp_function = interp1d(scaled_sim_x, sim_y, kind='linear', bounds_error=False)
unconv_response = (interp_function(meas_x)-vacuum_property)*sample['rescaling']+vacuum_property
#}}}
print " Plot the graph"#{{{
## Plot
if 'imag' in property_['name'].lower(): plotsign = -1
else: plotsign = 1
ax = plt.subplot(len(samples)*10 + len(properties)*100 + samples.index(sample) +
len(properties)*properties.index(property_) + 1)
last_row= (properties.index(property_) == len(properties)-1)
last_column= (samples.index(sample) == len(samples)-1)
ax.plot(meas_x, meas_y*plotsign, color=sample['color'], label="Experiment",
linewidth=0, marker='o', markersize=3)
ax.plot(meas_x, total_response_n/total_bins_weight*sample['rescaling']*plotsign+vacuum_property*plotsign,
color='black', label="Simulation", linewidth=1.5, linestyle=('-','--','-.',':')[0])
ax.plot(meas_x, unconv_response*plotsign, color='r', label="Single size",
linewidth=1, linestyle=('-','--','-.',':')[0])
## Annotate
if not last_row:
ax.text(.95, 0.0, '"'+sample['name']+'" sample',
bbox=dict(boxstyle="round,pad=0.1", fc="white", ec="white", lw=.4))
if last_row:
if last_column: ax.legend(loc=(.55,.1))
ax.set_xlabel(u"Frequency [THz]")
ax.grid(True)
ax.set_ylabel(property_['symbol'])
ax.set_xlim((0.2, 1.459))
ax.set_ylim(property_['ylim'])
#}}}
print " Finish the graph"
#plt.savefig("3EOS_convolution_elmajminmin-f-"+property_['name']+"_pow"+`filling_factor_power`+".pdf", bbox_inches='tight')
plt.savefig("mm2012_convolution.pdf", bbox_inches='tight')
#plt.savefig("3EOS_convolution_eps094_pow0.png", bbox_inches='tight')
Тем не менее, я получил это, что не то же самое. Токовый выход: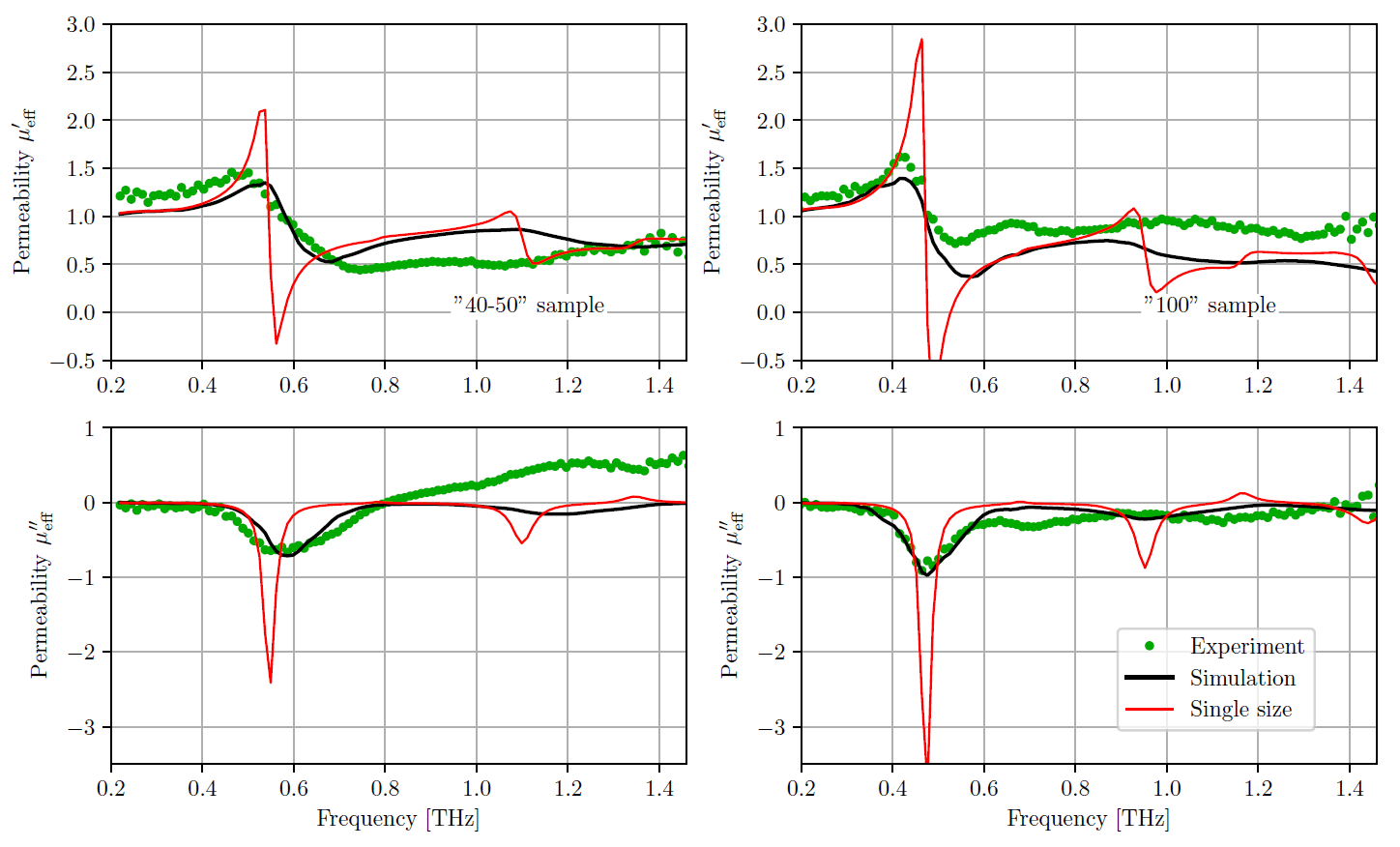
Не могли бы вы мне помочь? Спасибо.
1 ответ
Решение
Похоже, вы в целом недовольны тем, как matplotlib 2.0 обрабатывает прорисовку. Таким образом, вы можете использовать классический стиль
plt.style.use('classic')
и посмотрите, насколько результат больше соответствует вашим пожеланиям. Для любых оставшихся отличий, пожалуйста, обновите свой вопрос.