Самые длинные совпадения префиксов для URL
Мне нужна информация о любом стандартном пакете Python, который можно использовать для "совпадения самого длинного префикса" в URL. Я прошел через два стандартных пакета http://packages.python.org/PyTrie/ & 'http://pypi.python.org/pypi/trie/0.1.1', но они не кажутся быть полезным для самой длинной задачи поиска префикса в URL.
Например, если в моем наборе есть эти URL-адреса 1->http://www.google.com/mail, 2->http://www.google.com/document, 3->http://www.facebook.com, так далее..
Теперь, если я ищу "http://www.google.com/doc", он должен возвращать 2, а поиск "http: //www.face" должен возвращать 3.
Я хотел подтвердить, есть ли какой-нибудь стандартный пакет Python, который может помочь мне в этом, или я должен реализовать Trie для сопоставления префиксов.
Я не ищу решение с регулярным выражением, так как оно не масштабируется по мере увеличения количества URL.
Большое спасибо.
4 ответа
Этот пример хорош для небольших списков URL, но не очень хорошо масштабируется.
def longest_prefix_match(search, urllist):
matches = [url for url in urllist if url.startswith(search)]
if matches:
return max(matches, key=len)
else:
raise Exception("Not found")
Реализация с использованием модуля Trie.
import trie
def longest_prefix_match(prefix_trie, search):
# There may well be a more elegant way to do this without using
# "hidden" method _getnode.
try:
return list(node.value for node in prefix_trie._getnode(search).walk())
except KeyError:
return list()
url_list = [
'http://www.google.com/mail',
'http://www.google.com/document',
'http://www.facebook.com',
]
url_trie = trie.Trie()
for url in url_list:
url_trie[url] = url
searches = ("http", "http://www.go", "http://www.fa", "http://fail")
for search in searches:
print "'%s' ->" % search, longest_prefix_match(url_trie, search)
Результат:
'http' -> ['http://www.facebook.com', 'http://www.google.com/document', 'http://www.google.com/mail']
'http://www.go' -> ['http://www.google.com/document', 'http://www.google.com/mail']
'http://www.fa' -> ['http://www.facebook.com']
'http://fail' -> []
или используя PyTrie, который дает тот же результат, но списки упорядочены по-разному.
from pytrie import StringTrie
url_list = [
'http://www.google.com/mail',
'http://www.google.com/document',
'http://www.facebook.com',
]
url_trie = StringTrie()
for url in url_list:
url_trie[url] = url
searches = ("http", "http://www.go", "http://www.fa", "http://fail")
for search in searches:
print "'%s' ->" % search, url_trie.values(prefix=search)
Я начинаю думать, что радикальное дерево / дерево Патриции было бы лучше с точки зрения использования памяти. Вот как будет выглядеть основное дерево:
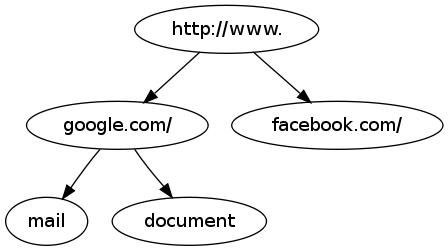
Принимая во внимание, что дерево больше похоже на:
Сравнение производительности
suffixtree против pytrie против trie против datrie против startswith -функции
Настроить
Записанное время является минимальным временем среди 3 повторений 1000 поисков. Время создания дерева включено и распределено по всем поискам. Поиск осуществляется по коллекциям имен хостов от 1 до 1000000 наименований.
Три типа строки поиска:
non_existent_key- нет соответствия для строкиrare_key- около 20 на миллионfrequent_key- количество вхождений сопоставимо с размером коллекции
Результаты
Максимальное потребление памяти на миллион URL:| function | memory, | ratio |
| | GiB | |
|-------------+---------+-------|
| suffix_tree | 0.853 | 1.0 |
| pytrie | 3.383 | 4.0 |
| trie | 3.803 | 4.5 |
| datrie | 0.194 | 0.2 |
| startswith | 0.069 | 0.1 |
#+TBLFM: $3=$2/@3$2;%.1f
Чтобы воспроизвести результаты, запустите тестовый код Trie.
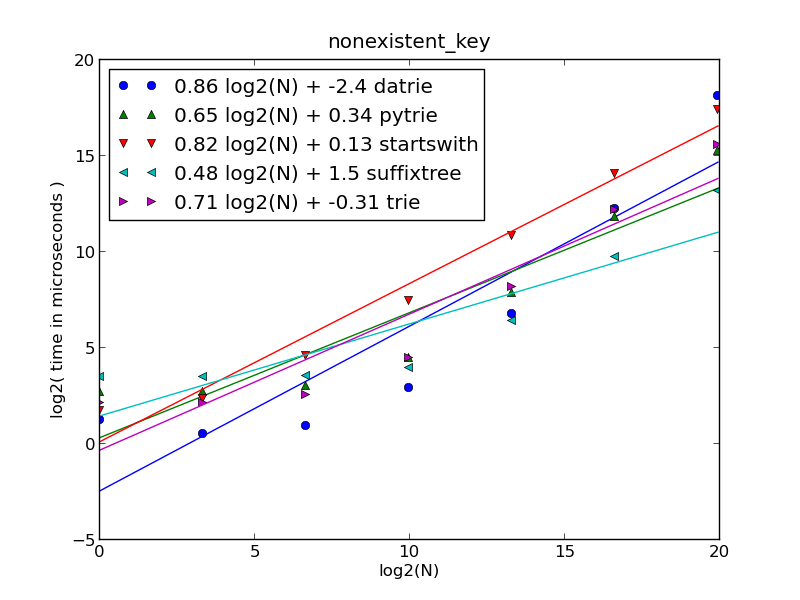
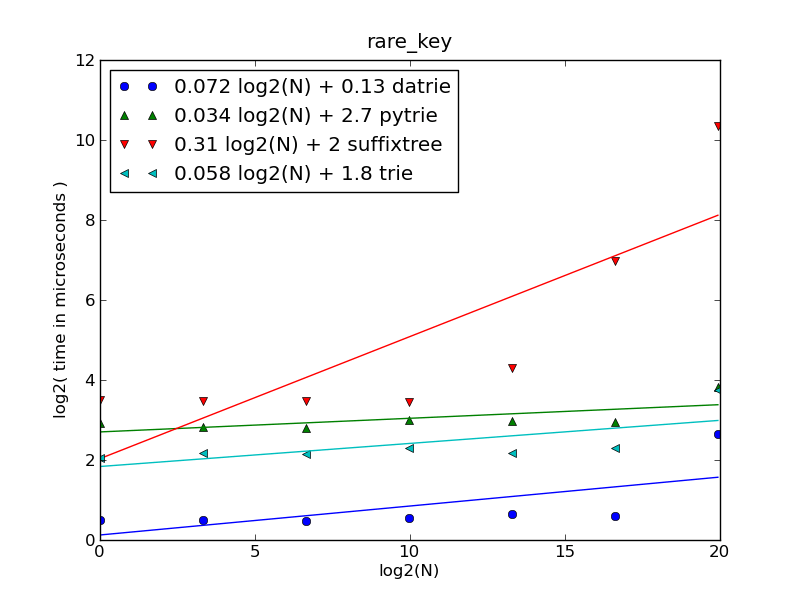
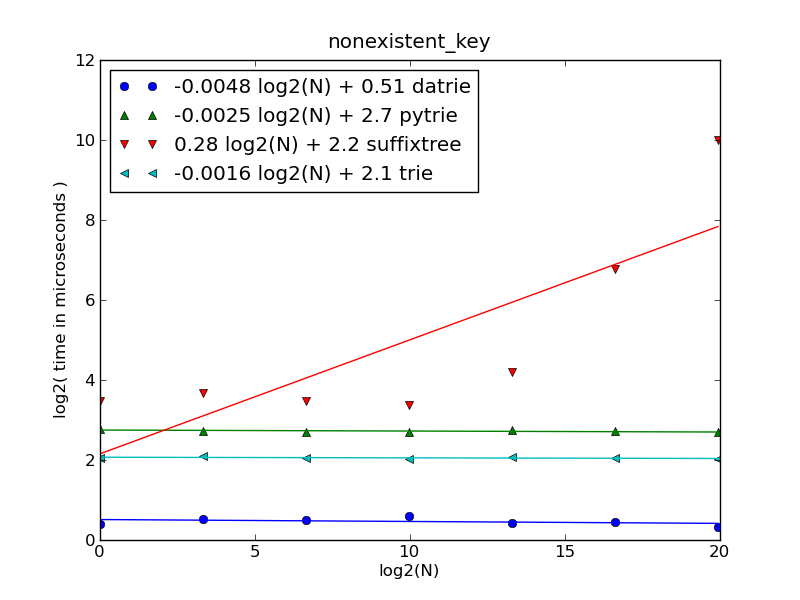
случай редкого ключа / несуществующего ключа
если количество URL-адресов меньше 10000, то Datrie является самым быстрым, для N>10000 -
suffixtreeбыстрее,startwithзначительно медленнее в среднем.
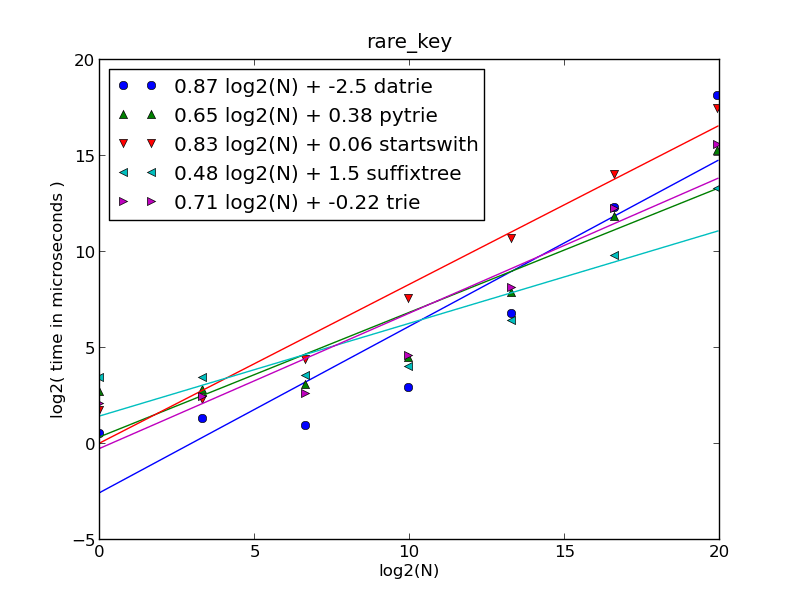
оси:
- вертикальная (временная) шкала составляет ~1 секунду (2**20 микросекунд)
- Горизонтальная ось показывает общее количество URL в каждом случае: N= 1, 10, 100, 1000, 10000, 100000 и 1000000 (миллион).
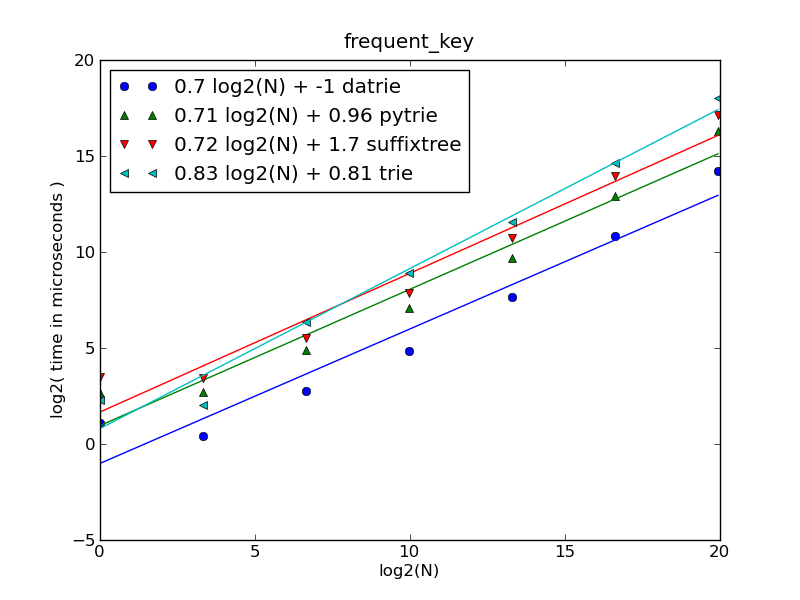
frequent_key
До N=100000
datrieявляется самым быстрым (для миллиона URL-адресов время доминирует время создания дерева).Наибольшее время занимает нахождение самого длинного совпадения среди найденных совпадений. Таким образом, все функции ведут себя как ожидалось.
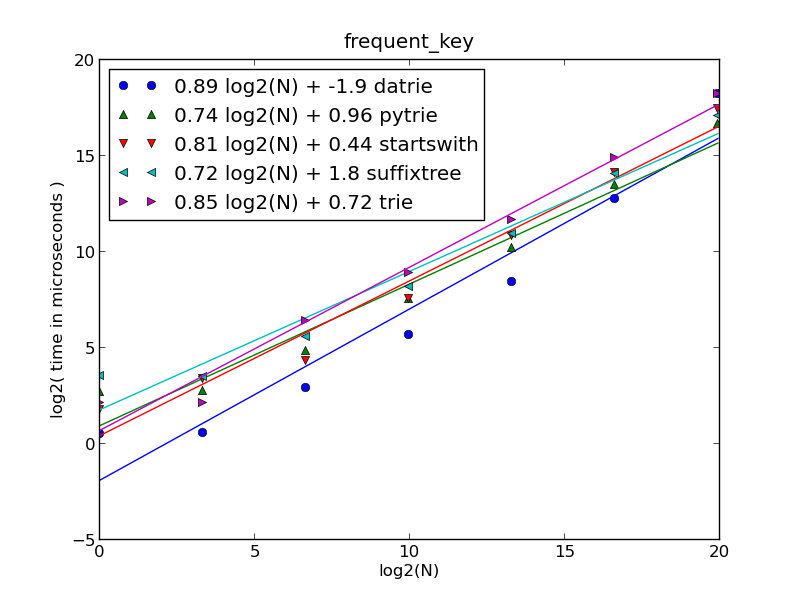
startswith - время выполнения не зависит от типа ключа.
trie а также pytrie вести себя подобно друг другу.
Производительность без времени строительства
datrie- самое быстрое, достойное потребление памятиstartswithЭто еще более неблагоприятно, потому что другие подходы не оштрафованы временем, которое требуется для построения дерева.datrie,pytrie,trie- почти O(1) (постоянное время) для редкого / несуществующего ключа
Подгонка (аппроксимация) полиномов известных функций для сравнения (тот же лог / логарифмическая шкала, что и на рисунках):
| Fitting polynom | Function |
|------------------------------+-------------------|
| 0.15 log2(N) + 1.583 | log2(N) |
| 0.30 log2(N) + 3.167 | log2(N)*log2(N) |
| 0.50 log2(N) + 1.111e-15 | sqrt(N) |
| 0.80 log2(N) + 7.943e-16 | N**0.8 |
| 1.00 log2(N) + 2.223e-15 | N |
| 2.00 log2(N) + 4.446e-15 | N*N |
Если вы готовы обменять оперативную память на время производительности, то SuffixTree может быть полезным. У этого есть хорошие алгоритмические свойства, такие как это позволяет решить самую длинную общую проблему подстроки за линейное время.
Если вы всегда ищете префикс, а не произвольную подстроку, вы можете добавить уникальный префикс при заполнении SubstringDict():
from SuffixTree import SubstringDict
substr_dict = SubstringDict()
for url in URLS: # urls must be ascii (valid urls are)
assert '\n' not in url
substr_dict['\n'+url] = url #NOTE: assume that '\n' can't be in a url
def longest_match(url_prefix, _substr_dict=substr_dict):
matches = _substr_dict['\n'+url_prefix]
return max(matches, key=len) if matches else ''
Такое использование SuffixTree кажется неоптимальным, но это в 20-150 раз быстрее (без SubstringDict() время строительства), чем решение @StephenPaulger [которое основано на .startswith() ] на данных, которые я пробовал, и это может быть достаточно хорошо.
Установить SuffixTree, бежать:
pip install SuffixTree -f https://hkn.eecs.berkeley.edu/~dyoo/python/suffix_trees
Функция ниже вернет индекс самого длинного соответствия. Другая полезная информация также может быть легко извлечена.
from os.path import commonprefix as oscp
def longest_prefix(s, slist):
pfx_idx = ((oscp([s, url]), i) for i, url in enumerate(slist))
len_pfx_idx = map(lambda t: (len(t[0]), t[0], t[1]), pfx_idx)
length, pfx, idx = max(len_pfx_idx)
return idx
slist = [
'http://www.google.com/mail',
'http://www.google.com/document',
'http://www.facebook.com',
]
print(longest_prefix('http://www.google.com/doc', slist))
print(longest_prefix('http://www.face', slist))