Найдите две точки на оси x, соответствующие пересечениям для cdf

Question

Соответствующий r code дается ниже.

theta <- seq(0,1, length = 10)
CD_theta <- function(x, p, n){
  1 - pbinom(x, size = n, prob = p) + 1 / 2 * dbinom(x, size = n, prob = p)
}

Затем я получил данные следующим образом:

mytheta <- CD_theta(5, theta, 10)
df <- data.frame(theta = theta, mytheta = mytheta)
ggplot(df, aes(x = theta, y = mytheta)) +
  geom_line(size = 1, col = "steelblue") +
  ylab("H(Theta)") +
  xlab("Theta")

Соответствующий график приведен ниже.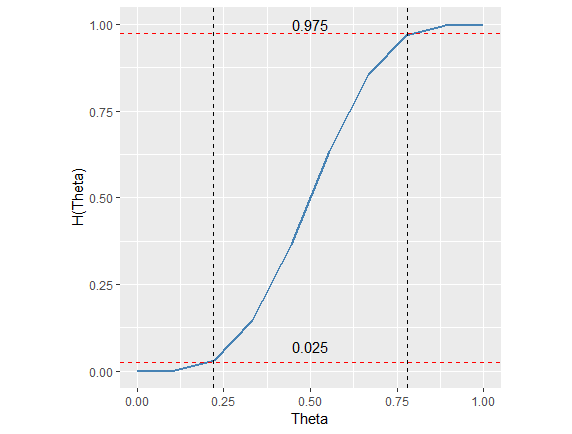

Как вы можете видеть, есть две горизонтальные линии (показаны красным цветом) и две вертикальные линии (показаны черным цветом). Мне нужно найти две точки на оси X, соответствующие пересечениям для H(тета).

Я использовал locator() функция в r вычислить два x перехвата для одной итерации. Я хотел бы повторить вышеизложенное 1000 раз, поэтому очень утомительно подходить к их поиску отдельно.

есть ли другие r функции могут быть использованы, чтобы найти эти две точки пересечения х?

Заранее спасибо.

Answer 1

Вот численный подход с использованием optimize функция:

library(reprex)

theta <- seq(0,1, length = 10)
CD_theta <- function(x, p, n){
  1 - pbinom(x, size = n, prob = p) + 1 / 2 * dbinom(x, size = n, prob = p)
}

# Create a function to compute the difference between the "y" you want 
# and the "y" computed with CD_theta function 
# then try to minimize the output of this new function : 
# get the theta value corresponding to this "y"

my_fn <- function(theta_loc, y, x, n) { 
  # the function to optimize
  abs(y - CD_theta(x, theta_loc, n)) # dont forget abs (absolute)
}

# Then use optimize function to compute the theta value 
# between a given interval : c(0,1) in this case
# Note that you can directly modify here the values of y, x and n
v1 <- optimize(my_fn, c(0, 1), y = 0.025, x = 5, n = 10)$`minimum` 
v2 <- optimize(my_fn, c(0, 1), y = 0.975, x = 5, n = 10)$`minimum` 

# print the results
v1 # 0.025
#> [1] 0.2120079
v2 # 0.975
#> [1] 0.7879756

Создано 2018-09-21 с помощью пакета представительства (v0.2.0).

Answer 2

Если вы хотите найти точный Theta а также HTheta значения, не зависящие от размера сетки (здесь N = 10), применять uniroot к CD_theta функция.

CD_theta <- function(x, p, n) {
    1  -  pbinom (x, size = n, prob = p) + 
    1/2 * dbinom(x, size = n, prob = p)
}

u1 = uniroot(function(p) CD_theta(5, p, 10) - 0.025, c(0, 1))
u2 = uniroot(function(p) CD_theta(5, p, 10) - 0.975, c(0, 1))
(Theta1 = u1$root)  # 0.2119934
(Theta2 = u2$root)  # 0.7880066

Но если дискретизация (с N = 10), а затем выполните линейную интерполяцию этой функции между точками сетки.

theta <- seq(0, 1, length = 10)
mytheta <- CD_theta(5, theta, 10)
f <- approxfun(theta, mytheta, method = "linear", 0.0, 1.0)

u1 = uniroot(function(p) f(p) - 0.025, c(0, 1))
u2 = uniroot(function(p) f(p) - 0.975, c(0, 1))
(Theta1 = u1$root)  # 0.2015638
(Theta2 = u2$root)  # 0.7984362

Answer 3

Немного увеличивая дискретизацию вашей кривой, это становится довольно простым:

theta <- seq(0,1, length = 100) # increase length here for more precision on point locations
CD_theta <- function(x, p, n){
  1 - pbinom(x, size = n, prob = p) + 1 / 2 * dbinom(x, size = n, prob = p)
}

mytheta <- CD_theta(5, theta, 10)
df <- data.frame(theta = theta, mytheta = mytheta)
ggplot(df, aes(x = theta, y = mytheta)) +
  geom_line(size = 1, col = "steelblue") +
  ylab("H(Theta)") +
  xlab("Theta")

points <- data.frame(x=c(theta[which.min(abs(mytheta - .975))], # find which point is the nearer
                         theta[which.min(abs(mytheta - .025))]),
                     y=c(.975,.025))

ggplot(df, aes(x = theta, y = mytheta)) +
  geom_line(size = 1, col = "steelblue") +
  ylab("H(Theta)") +
  xlab("Theta") + 
  geom_point(data=points,aes(y=y, x=x), size=5, col="red")