Дизайн DFA принимает двоичные строки, делимые на число 'n'
Мне нужно научиться проектировать DFA таким образом, чтобы при любом числе n он принимал двоичные строки { 0,1 }, десятичное эквивалентное число которых делится на n. Для разных n будут разные DFA, но может ли кто-нибудь дать базовый подход, которому я должен следовать, чтобы перейти к любому числу 0
3 ответа
Ниже я написал ответ для n равно 5, но вы можете применить тот же подход, чтобы нарисовать DFA для любого значения n и "любая позиционная система счисления", например, двоичная, троичная...
Сначала используйте термин "Полная DFA", DFA, определенный для полной области в δ:Q × Σ→Q, называется "Полная DFA". Другими словами, мы можем сказать; в диаграмме переходов полного DFA отсутствует пропущенное ребро (например, из каждого состояния в Q имеется один исходящий ребро для каждого символа языка в Σ). Примечание. Иногда мы определяем частичный DFA как δ ⊆ Q × Σ→Q (читай: как "δ:Q × Σ→Q" читается в определении DFA).
Дизайн DFA принимает двоичные числа, делимые на число 'n':
Шаг 1: Когда вы делите число ω на n тогда напоминание может быть 0, 1, ..., (n - 2) или (n -1). Если остаток 0 это означает, что ω делится на n в противном случае нет. Таким образом, в моем DFA будет состояние q r, которое будет соответствовать значению остатка r, где 0 <= r <= (n - 1) и общее количество штатов в DFA n,
После обработки числовой строки ω над Σ конечное состояние q r означает, что ω % n => r (оператор напоминания%).
В любом автомате назначение состояния подобно элементу памяти. Состояние в атоме хранит некоторую информацию, такую как переключатель вентилятора, которая может сказать, находится ли вентилятор в выключенном или включенном состоянии. Для n = 5 пять состояний в DFA соответствуют пяти данным напоминания следующим образом:
- Состояние q 0 достигается, если напоминание равно 0. Состояние q 0 является конечным состоянием (состояние принятия). Это также начальное состояние.
- Состояние q 1 достигает, если напоминание равно 1, неконечное состояние.
- Состояние q 2, если напоминание равно 2, не является окончательным состоянием.
- Состояние q 3, если напоминание равно 3, не является окончательным состоянием.
- Состояние q 4, если напоминание равно 4, не является окончательным состоянием.
Используя приведенную выше информацию, мы можем начать рисовать диаграмму переходов TD из пяти состояний следующим образом:
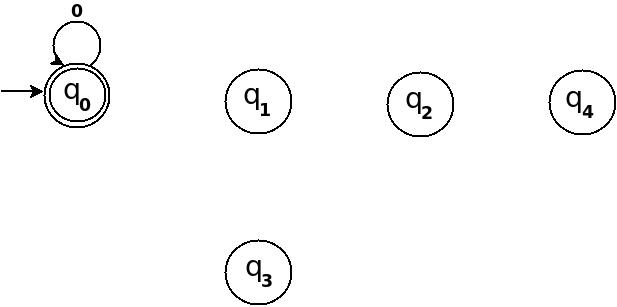
Рисунок 1
Итак, 5 состояний для 5 оставшихся значений. После обработки строки ω, если конечное состояние становится q 0, это означает, что десятичный эквивалент входной строки делится на 5. На приведенном выше рисунке q 0 обозначено конечное состояние в виде двух концентрических окружностей.
Кроме того, я определил правило перехода δ: (q 0, 0) → q 0 как собственный цикл для символа '0' в состоянии q 0 это происходит потому, что десятичный эквивалент любой строки состоит только из '0' 0 и 0 делится на n,
Шаг 2: TD выше не завершен; и может обрабатывать только строки '0' s. Теперь добавьте еще несколько ребер, чтобы он мог обрабатывать строки следующего числа. Проверьте таблицу ниже, показывает новые правила перехода, которые могут быть добавлены следующим шагом:
┌──────┬──────┬─────────────┬─────────┐ │ Число │ Двоичный код │ Остаток (% 5) │ Конечное состояние │ ├──────┼──────┼─────────────┼─────────┤ Ne один │1 │1 │q 1 │ ├──────┼──────┼─────────────┼─────────┤ │Два │10 │2 │q 2 │ ├──────┼──────┼─────────────┼─────────┤ │Три │11 │3 │q 3 │ ├──────┼──────┼─────────────┼─────────┤ OurFour │100 │4 │q 4 │ └──────┴──────┴─────────────┴─────────┘
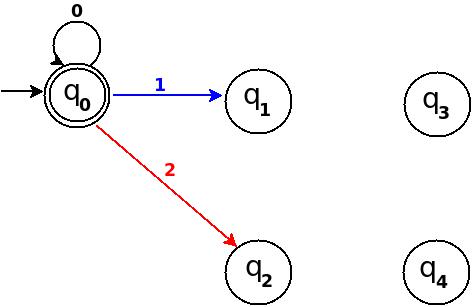
- Обрабатывать двоичную строку
'1'должно быть правило перехода δ: (q 0, 1) → q 1 - Два:- двоичное представление
'10'конечное состояние должно быть q 2, и обрабатывать'10'нам просто нужно добавить еще одно правило перехода δ: (q 1, 0) → q 2
Путь: → (q 0) ─1 → (q 1) ─0 → (q 2) - Три:- в двоичном виде это
'11'конечное состояние равно q 3, и нам нужно добавить правило перехода δ: (q 1, 1) → q 3
Путь: → (q 0) ─1 → (q 1) ─1 → (q 3) - Четыре:- в двоичном
'100'конечное состояние q 4. TD уже обрабатывает строку префикса'10'и нам просто нужно добавить новое правило перехода δ: (q 2, 0) → q 4
Путь: → (q 0) ─1 → (q 1) ─0 → (q 2) ─0 → (q 4)
Фигура 2
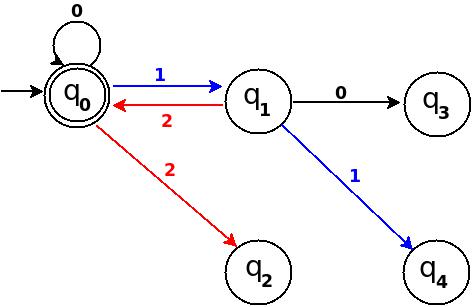
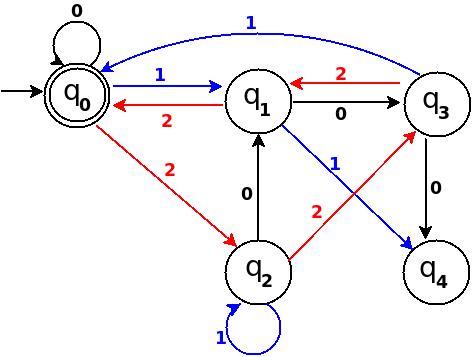
Шаг 3: Пять = 101
Вышеприведенная диаграмма переходов на рисунке 2 по-прежнему неполна и имеется много пропущенных ребер, например, для δ переход не определен: (q 2, 1) - ?, И правило должно присутствовать для обработки строк, таких как '101',
Так как '101' = 5 делится на 5, и принять '101' Я добавлю δ: (q 2, 1) → q 0 на рисунке 2 выше.
Путь: → (q 0) ─1 → (q 1) ─0 → (q 2) ─1 → (q 0)
с этим новым правилом диаграмма перехода становится следующей:
Рис-3
Ниже на каждом шаге я выбираю следующее последующее двоичное число, чтобы добавить отсутствующее ребро, пока не получу TD в качестве "полного DFA".
Шаг 4: Шесть = 110.
Мы можем обработать '11' в настоящем ТД на рисунке 3 как: → (q 0) ─11 → (q 3) ─0 → (?). Поскольку 6 % 5 = 1, это означает добавление одного правила δ: (q 3, 0) → q 1.
Рисунок-4
Шаг 5: Семь = 111
┌──────┬──────┬─────────────┬─────────┬─────────── ─┬───────────┐ │ Число │ Двоичный код │ Остаток (% 5) │ Конечное состояние │ Путь │ Добавить │ ├──────┼──────┼─────────────┼─────────┼────────────┼───────────┤ E Семена │111 │7% 5 = 2 │q 2 │ q 0 ─11 → q 3 │ q 3 ─1 → q 2 │ └──────┴──────┴─────────────┴─────────┴─────────── ─┴───────────┘
Рис-5
Шаг 6: Восемь = 1000
┌──────┬──────┬─────────────┬─────────┬──────────┬ ─────────┐ │ Число │ Двоичный код │ Остаток (% 5) │ Конечное состояние │ Путь │ Добавить │ ├──────┼──────┼─────────────┼─────────┼──────────┼─────────┤ │ Восемь │1000 │8% 5 = 3 │q 3 │q 0 ─100 → q 4 │ q 4 ─0 → q 3 │ └──────┴──────┴─────────────┴─────────┴──────────┴ ─────────┘
Рис-6
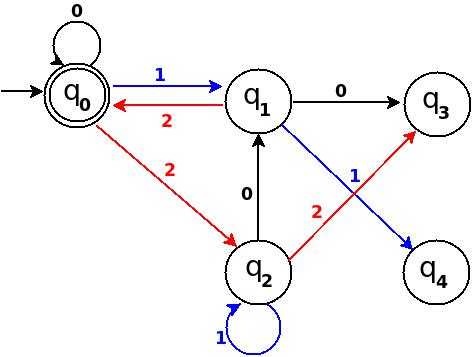
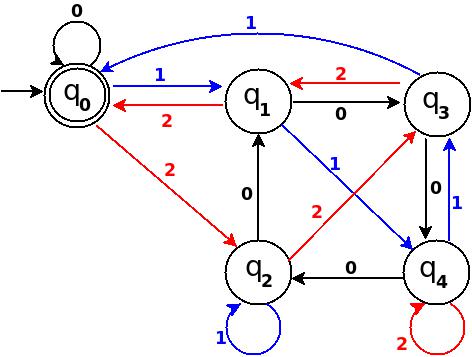
Шаг 7: Девять = 1001
┌──────┬──────┬─────────────┬─────────┬──────────┬ ─────────┐ │ Число │ Двоичный код │ Остаток (% 5) │ Конечное состояние │ Путь │ Добавить │ ├──────┼──────┼─────────────┼─────────┼──────────┼ ─────────┤ Ine Девять │1001 │9% 5 = 4 │q 4 │q 0 ─100 → q 4 │ q 4 ─1 → q 4 │ └──────┴──────┴─────────────┴─────────┴──────────┴ ─────────┘
Рис-7
В TD-7 общее число ребер равно 10 == Q × Σ = 5 × 2. И это полный DFA, который может принимать все возможные двоичные строки, для которых десятичный эквивалент делится на 5.
Конструкция DFA принимает троичные числа, кратные числу n:
Шаг-1 Точно так же, как для двоичного файла, используйте рисунок-1.
Шаг 2 Добавьте ноль, один, два
┌───────┬───────┬─────────────┬─────────┬──────────────┐ │ десятичный │ троичный main остаток (% 5) │ конечное состояние │ добавить │ ├───────┼───────┼─────────────┼─────────┼──────────────┤ │Zero │0 │0 │q0 │ δ:(q0,0)→q0 │ ├───────┼───────┼─────────────┼─────────┼──────────────┤ Ne Один │1 │1 │q1 │ δ:(q0,1)→q1 │ ├───────┼───────┼─────────────┼─────────┼──────────────┤ │Два │2 │2 │q2 │ δ:(q0,2)→q3 │ └───────┴───────┴─────────────┴─────────┴──────────────┘
Рис-8
Шаг 3 Добавьте три, четыре, пять
┌───────┬───────┬─────────────┬─────────┬─────────────┐ │ Десятичный │ Тройной │ Остаток (% 5) │ Конечное состояние │ Добавить │ ├───────┼───────┼──────┼─────────── ──┼─────────┼─────────────┤ │ Три │10 │3 │q3 │ δ:(q1,0)→q3 │ ├───────┼───────┼─────────────┼─────────┼───────────── Our │ Четвертый │11 │4 │q4 │ δ:(q1,1)→q4 │ ├───────┼────────────────────────────┼─────────┼─────────────┤ │Five │12 │0 │q0 │ δ:(q1,2)→q0 │ └───────┴───────┴─────────────┴─────────┴─────────────┘
Рис-9
Шаг 4 Добавьте шесть, семь, восемь
┌───────┬───────┬─────────────┬─────────┬───────── ────┐ │ десятичный │ троичный main остаток (% 5) │ конечное состояние │ добавить │ ├───────┼───────┼─────────────┼─────────┼─────────────┤ IxSix │20 │1 │q1 │ δ:(q2,0)→q1 │ ├───────┼───────┼─────────────┼─────────┼─────────────┤ E Семена │21 │2 │q2 │ δ:(q2,1)→q2 │ ├───────┼───────┼─────────────┼─────────┼─────────────┤ │ Восемь │22 │3 │q3 │ δ:(q2,2)→q3 │ └───────┴───────┴─────────────┴─────────┴─────────────┘
Рис-10
Шаг 5 Добавьте девять, десять, одиннадцать
┌───────┬───────┬─────────────┬─────────┬─────────────┐ │ Десятичный │ Тройной │ Остаток (% 5) │ Конечное состояние │ Добавить │ ├───────┼───────┼──────┼─────────── ──┼─────────┼─────────────┤ ine Девять │100 │4 │q4 │ δ:(q3,0)→q4 │ ├───────┼───────┼─────────────┼─────────┼─────────────┤ │ Десять │101 │0 │q0 │ δ:(q3,1)→q0 │ ├───────┼──────────────────────────── ┼─────────┼─────────────┤ leEleven │102 │1 │q1 │ δ:(q3,2)→q1 │ └───────┴───────┴─────────────┴─────────┴─────────────┘
Рис-11
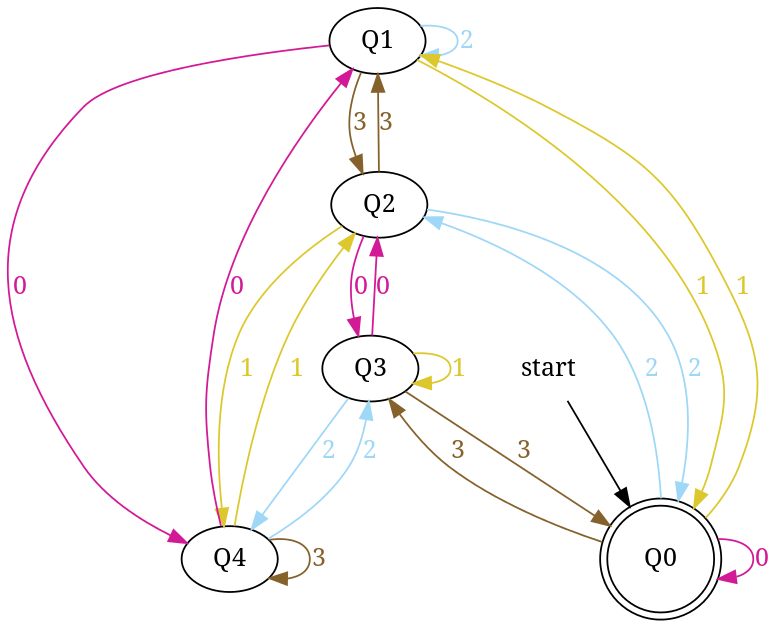
Шаг 6 Добавьте двенадцать, тринадцать, четырнадцать
┌────────┬───────┬─────────────┬─────────┬─────────────┐ │ десятичный │ троичный main остаток (% 5) │ конечное состояние │ добавить │ ├────────┼───────┼─────────────┼─────────┼─────────────┤ │ Двенадцать 10110 │2 │q2 │ δ:(q4,0)→q2 │ ├────────┼───────┼─────────────┼─────────┼─────────────┤ │ тринадцать│111 │3 │q3 │ δ:(q4,1)→q3 │ ├────────┼───────┼─────────────┼─────────┼─────────────┤ │Четырнадцать│112 │4 │q4 │ δ:(q4,2)→q4 │ └────────┴───────┴─────────────┴─────────┴─────────────┘
Рис-12
Общее число ребер в диаграмме перехода на рисунке 12 составляет 15 = Q × Σ = 5 * 3 (полный DFA). И этот DFA может принять все строки, состоящие из {0, 1, 2}, эти десятичные эквиваленты делятся на 5.
Если вы заметили на каждом шаге, в таблице есть три записи, потому что на каждом шаге я добавляю все возможные исходящие ребра из состояния, чтобы сделать полный DFA (и я добавляю ребро, так что состояние q r становится для остатка r)!
Чтобы добавить дальше, помните, что объединение двух обычных языков также является регулярным. Если вам нужно спроектировать DFA, который принимает двоичные строки, эти десятичные эквиваленты делятся на 3 или 5, затем нарисуйте два отдельных DFA для делимых на 3 и 5, а затем объедините оба DFA для построения целевого DFA (для 1 <= n <= 10 Вы должны объединить 10 ДФА).
Если вас попросят нарисовать DFA, который принимает двоичные строки, так что десятичный эквивалент делится на 5 и 3, то вы ищете DFA, кратный 15 (но как насчет 6 и 8?).
Примечание: DFA, полученные с помощью этого метода, будут минимизированы DFA, только если между числом нет общего фактора n и основание, например, между 5 и 2 в первом примере или между 5 и 3 во втором примере, следовательно, оба DFA, построенные выше, являются минимизированными DFA. Если вам интересно читать дальше о возможных мини состояниях для номера n и база b читать статью: делимость и сложность государства.
ниже я добавил скрипт Python, я написал его для удовольствия, изучая Python-библиотеку Python. Я добавляю это, я надеюсь, что это может быть полезно для кого-то в некотором роде.
Разработайте DFA для базовых числовых строк "b", делимых на число "n":
Таким образом, мы можем применить вышеописанный трюк, чтобы нарисовать DFA для распознавания числовых строк в любой базе. 'b' те, которые делятся на данное число 'n', В этом DFA общее количество штатов будет n (за n остатки) и количество ребер должно быть равно 'b' * 'n' - то есть полное DFA: 'b' = количество символов на языке DFA и 'n' = количество состояний.
Используя вышеприведенный трюк, ниже я написал скрипт Python для рисования DFA для ввода base а также number, В сценарии функция divided_by_N заполняет правила перехода DFA в base * number шаги. В каждом шаге я конвертирую num в числовую строку num_s используя функцию baseN(), Чтобы избежать обработки каждой числовой строки, я использовал временную структуру данных lookup_table, На каждом шаге конечное состояние для числовой строки num_s оценивается и сохраняется в lookup_table использовать в следующем шаге.
Для графа переходов DFA я написал функцию draw_transition_graph используя библиотеку Pygraphviz (очень прост в использовании). Для использования этого скрипта вам необходимо установить graphviz, Чтобы добавить цветные ребра в диаграмму перехода, я случайным образом генерирую цветовые коды для каждого символа get_color_dict функция.
#!/usr/bin/env python
import pygraphviz as pgv
from pprint import pprint
from random import choice as rchoice
def baseN(n, b, syms="0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"):
""" converts a number `n` into base `b` string """
return ((n == 0) and syms[0]) or (
baseN(n//b, b, syms).lstrip(syms[0]) + syms[n % b])
def divided_by_N(number, base):
"""
constructs DFA that accepts given `base` number strings
those are divisible by a given `number`
"""
ACCEPTING_STATE = START_STATE = '0'
SYMBOL_0 = '0'
dfa = {
str(from_state): {
str(symbol): 'to_state' for symbol in range(base)
}
for from_state in range(number)
}
dfa[START_STATE][SYMBOL_0] = ACCEPTING_STATE
# `lookup_table` keeps track: 'number string' -->[dfa]--> 'end_state'
lookup_table = { SYMBOL_0: ACCEPTING_STATE }.setdefault
for num in range(number * base):
end_state = str(num % number)
num_s = baseN(num, base)
before_end_state = lookup_table(num_s[:-1], START_STATE)
dfa[before_end_state][num_s[-1]] = end_state
lookup_table(num_s, end_state)
return dfa
def symcolrhexcodes(symbols):
"""
returns dict of color codes mapped with alphabets symbol in symbols
"""
return {
symbol: '#'+''.join([
rchoice("8A6C2B590D1F4E37") for _ in "FFFFFF"
])
for symbol in symbols
}
def draw_transition_graph(dfa, filename="filename"):
ACCEPTING_STATE = START_STATE = '0'
colors = symcolrhexcodes(dfa[START_STATE].keys())
# draw transition graph
tg = pgv.AGraph(strict=False, directed=True, decorate=True)
for from_state in dfa:
for symbol, to_state in dfa[from_state].iteritems():
tg.add_edge("Q%s"%from_state, "Q%s"%to_state,
label=symbol, color=colors[symbol],
fontcolor=colors[symbol])
# add intial edge from an invisible node!
tg.add_node('null', shape='plaintext', label='start')
tg.add_edge('null', "Q%s"%START_STATE,)
# make end acception state as 'doublecircle'
tg.get_node("Q%s"%ACCEPTING_STATE).attr['shape'] = 'doublecircle'
tg.draw(filename, prog='circo')
tg.close()
def print_transition_table(dfa):
print("DFA accepting number string in base '%(base)s' "
"those are divisible by '%(number)s':" % {
'base': len(dfa['0']),
'number': len(dfa),})
pprint(dfa)
if __name__ == "__main__":
number = input ("Enter NUMBER: ")
base = input ("Enter BASE of number system: ")
dfa = divided_by_N(number, base)
print_transition_table(dfa)
draw_transition_graph(dfa)
Выполните это:
~/study/divide-5/script$ python script.py
Enter NUMBER: 5
Enter BASE of number system: 4
DFA accepting number string in base '4' those are divisible by '5':
{'0': {'0': '0', '1': '1', '2': '2', '3': '3'},
'1': {'0': '4', '1': '0', '2': '1', '3': '2'},
'2': {'0': '3', '1': '4', '2': '0', '3': '1'},
'3': {'0': '2', '1': '3', '2': '4', '3': '0'},
'4': {'0': '1', '1': '2', '2': '3', '3': '4'}}
~/study/divide-5/script$ ls
script.py filename.png
~/study/divide-5/script$ display filename
Выход:
DFA принимает числовые строки в базе 4, которые делятся на 5
Аналогично, введите base = 4 и number = 7 для генерации - dfa принимает числовую строку в базе '4', которая делится на '7'
Кстати, попробуйте изменить filename в .png или же .jpeg,
Ссылки, которые я использую, чтобы написать этот скрипт:
➊ Функция baseN из "конвертировать целое число в строку в заданной числовой базе в Python"
➋ Для установки "pygraphviz": "Python не видит pygraphviz"
➌ Научиться использовать Pygraphviz: "Python-FSM"
➍ Чтобы сгенерировать случайные шестнадцатеричные цветовые коды для каждого символа языка: "Как бы я сделал генератор случайных шестнадцатеричных кодов, используя.join и для циклов?"
Я знаю, что довольно поздно, но я просто хотел добавить несколько вещей к уже правильному ответу, предоставленному @Grijesh. Я хотел бы просто отметить, что ответ @Grijesh не дает минимального DFA. Хотя ответ, безусловно, является правильным способом получения DFA, если вам нужен минимальный DFA, вам придется заглянуть в свой делитель.
Как, например, в двоичных числах, если делитель является степенью 2 (то есть 2^n), то минимальное количество требуемых состояний будет n+1. Как бы вы сконструировали такой автомат? Просто посмотрите свойства двоичных чисел. Для числа, скажем 8 (что равно 2^3), все его кратные будут иметь последние 3 бита равными 0. Например, 40 в двоичном виде - это 101000. Поэтому для того, чтобы язык мог принять любое число, кратное 8, нам просто нужно автомат, который видит, равны ли последние 3 бита 0, что мы можем сделать всего в 4 состояниях вместо 8 состояний. Это половина сложности машины.
Фактически это может быть распространено на любую базу. Для троичной базовой системы счисления, если, например, нам нужно спроектировать автомат для делимости на 9, нам просто нужно посмотреть, равны ли последние 2 числа входа 0. Что снова может быть сделано только в 3 состояниях.
Хотя, если делитель не такой уж особенный, нам нужно пройти только с ответом @ Grijesh. Как, например, в двоичной системе, если мы возьмем делители 3 или 7 или, может быть, 21, нам понадобится только такое количество состояний. Таким образом, для любого нечетного числа n в двоичной системе нам нужно n состояний, чтобы определить язык, который принимает все кратные n. С другой стороны, если число является четным, но не степенью 2 (только в случае двоичных чисел), то нам нужно разделить число на 2, пока мы не получим нечетное число, а затем мы можем найти минимальное число состояний по добавив нечетное число произведенное и количество раз мы делим на 2.
Например, если нам нужно найти минимальное количество состояний DFA, которое принимает все двоичные числа, кратные 20, мы делаем:
20/2 = 10
10/2 = 5
Следовательно, наш ответ 5 + 1 + 1 = 7, (1 + 1, потому что мы разделили число 20 дважды).
Вы можете создать DFA, используя простую модульную арифметику. Мы можем интерпретировать w которая является строкой k-арных чисел с использованием следующего правила
V[0] = 0
V[i] = (S[i-1] * k) + to_number(str[i])
V[|w|] это число, которое w представляет. Если изменить это правило, чтобы найти w mod Nправило становится таким.
V[0] = 0
V[i] = ((S[i-1] * k) + to_number(str[i])) mod N
и каждый V[i] является одним из числа от 0 до N-1, которое соответствует каждому состоянию в DFA. Мы можем использовать это как переход состояния.
Смотрите пример.
k = 2, N = 5
| V | (V*2 + 0) mod 5 | (V*2 + 1) mod 5 |
+---+---------------------+---------------------+
| 0 | (0*2 + 0) mod 5 = 0 | (0*2 + 1) mod 5 = 1 |
| 1 | (1*2 + 0) mod 5 = 2 | (1*2 + 1) mod 5 = 3 |
| 2 | (2*2 + 0) mod 5 = 4 | (2*2 + 1) mod 5 = 0 |
| 3 | (3*2 + 0) mod 5 = 1 | (3*2 + 1) mod 5 = 2 |
| 4 | (4*2 + 0) mod 5 = 3 | (4*2 + 1) mod 5 = 4 |
k = 3, N = 5
| V | 0 | 1 | 2 |
+---+---+---+---+
| 0 | 0 | 1 | 2 |
| 1 | 3 | 4 | 0 |
| 2 | 1 | 2 | 3 |
| 3 | 4 | 0 | 1 |
| 4 | 2 | 3 | 4 |
Теперь вы можете увидеть очень простой шаблон. Вы можете создать переход DFA, просто записав повторяющиеся числа слева направо, сверху вниз, от 0 до N-1.