Отрицательные веса с использованием алгоритма Дейкстры

Question

Я пытаюсь понять, почему алгоритм Дейкстры не будет работать с отрицательными весами. Читая пример по кратчайшим путям, я пытаюсь выяснить следующий сценарий:

    2
A-------B
 \     /
3 \   / -2
   \ /
    C

С веб-сайта:

Предполагая, что все ребра направлены слева направо, если мы начнем с A, алгоритм Дейкстры выберет ребро (A,x), минимизирующее d(A,A)+ длина (ребро), а именно (A,B). Затем он устанавливает d(A,B)=2 и выбирает другое ребро (y,C), минимизируя d(A,y)+d(y,C); единственный выбор - (A,C), и он устанавливает d(A,C)=3. Но он никогда не находит кратчайший путь от А до В через С общей длиной 1.

Я не могу понять, почему при использовании следующей реализации Дейкстры, d[B] не будет обновлен до 1 (Когда алгоритм достигнет вершины C, он выполнит релаксацию на B, увидим, что d [B] равно 2и, следовательно, обновите его значение до 1).

Dijkstra(G, w, s)  {
   Initialize-Single-Source(G, s)
   S ← Ø
   Q ← V[G]//priority queue by d[v]
   while Q ≠ Ø do
      u ← Extract-Min(Q)
      S ← S U {u}
      for each vertex v in Adj[u] do
         Relax(u, v)
}

Initialize-Single-Source(G, s) {
   for each vertex v  V(G)
      d[v] ← ∞
      π[v] ← NIL
   d[s] ← 0
}

Relax(u, v) {
   //update only if we found a strictly shortest path
   if d[v] > d[u] + w(u,v) 
      d[v] ← d[u] + w(u,v)
      π[v] ← u
      Update(Q, v)
}

Спасибо,

Меир

Answer 1

Алгоритм, который вы предложили, действительно найдет кратчайший путь в этом графе, но не во всех графах в целом. Например, рассмотрим этот график:

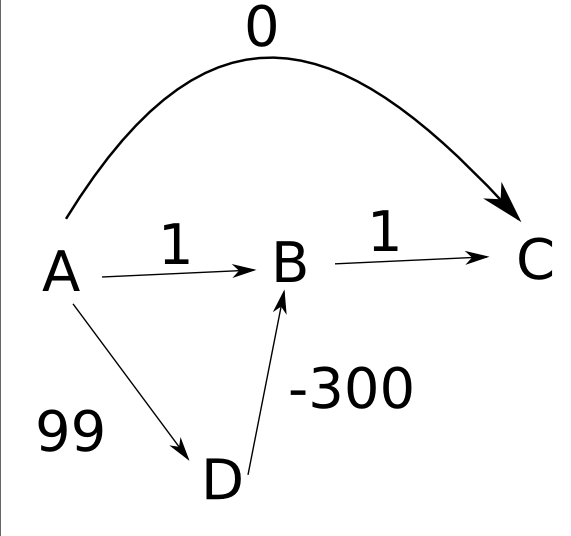
Предположим, что края направлены слева направо, как в вашем примере,

Ваш алгоритм будет работать следующим образом:

1. Во-первых, вы установили d(A) в zero и другие расстояния до infinity,
2. Затем вы расширяете узел A, настройка d(B) в 1, d(C) в zero, а также d(D) в 99,
3. Далее вы расширяете C, без чистых изменений.
4. Затем вы расширяетесь B, который не имеет никакого эффекта.
5. Наконец, вы расширяете D, который меняется d(B) в -201,

Обратите внимание, что в конце этого, что d(C) все еще 0хотя кратчайший путь к C имеет длину -200 , Таким образом, ваш алгоритм не может точно рассчитать расстояния в некоторых случаях. Более того, даже если вы должны хранить обратные указатели, говорящие, как добраться от каждого узла до начального узла A вы бы в конечном итоге пошли по неверному пути C в A,

Answer 2

Обратите внимание, что Дейкстра работает даже для отрицательных весов, если в графе нет отрицательных циклов, то есть циклов, у которых суммарный вес меньше нуля.

Конечно, можно спросить, почему в примере, созданном templatetypedef, Дейкстра терпит неудачу, даже если нет отрицательных циклов, даже не циклов. Это потому, что он использует другой критерий остановки, который содержит алгоритм, как только целевой узел достигнут (или все узлы были рассчитаны один раз, он не указал это точно). На графике без отрицательных весов это работает нормально.

Если использовать альтернативный критерий остановки, который останавливает алгоритм, когда очередь приоритетов (куча) пустует (этот критерий остановки также использовался в вопросе), тогда dijkstra найдет правильное расстояние даже для графиков с отрицательными весами, но без отрицательные циклы.

Однако в этом случае асимптотическая граница времени Дейкстры для графов без отрицательных циклов теряется. Это связано с тем, что ранее установленный узел может быть повторно вставлен в кучу, когда найдено лучшее расстояние из-за отрицательных весов. Это свойство называется исправлением метки.

Answer 3

TL;DR: Ответ зависит от вашей реализации. Для опубликованного вами псевдокода он работает с отрицательными весами.

---

Варианты алгоритма Дейкстры

Ключ в том, что существует 3 варианта реализации алгоритма Дейкстры, но все ответы на этот вопрос игнорируют различия между этими вариантами.

1. Использование вложенногоfor-петля для расслабления вершин. Это самый простой способ реализовать алгоритм Дейкстры. Временная сложность - O(V^2).
2. Реализация на основе очереди приоритетов / кучи + повторный вход НЕ разрешен, где повторный вход означает, что освобожденная вершина может быть снова помещена в очередь приоритета, чтобы ее можно было снова расслабить позже.
3. Реализация на основе очереди / кучи с приоритетом + повторный вход разрешен.

Версии 1 и 2 не будут работать на графиках с отрицательными весами (если вы получите правильный ответ в таких случаях, это просто совпадение), но версия 3 по-прежнему работает.

Псевдокод, опубликованный под исходной проблемой, - это версия 3 выше, поэтому он работает с отрицательными весами.

Вот хорошая ссылка из алгоритма (4-е издание), в котором говорится (и содержится java-реализация версий 2 и 3, о которых я упоминал выше):

В. Работает ли алгоритм Дейкстры с отрицательными весами?

А. Да и нет. Существует два алгоритма кратчайших путей, известных как алгоритм Дейкстры, в зависимости от того, может ли вершина быть поставлена ​​в очередь приоритетной очереди более одного раза. Когда веса неотрицательны, две версии совпадают (поскольку ни одна вершина не будет помещена в очередь более одного раза). Версия, реализованная в DijkstraSP.java (которая позволяет ставить вершину в очередь более одного раза), верна при наличии отрицательных весов ребер (но без отрицательных циклов), но время ее работы в худшем случае экспоненциально. (Отметим, что DijkstraSP.java выдает исключение, если взвешенный по ребрам орграф имеет ребро с отрицательным весом, так что программист не удивится этому экспоненциальному поведению.) Если мы изменим DijkstraSP.java так, чтобы вершина не могла быть поставлена ​​в очередь более одного раза (например, используя массив отмеченных [], чтобы отметить те вершины, которые были ослаблены),тогда алгоритм гарантированно будет работать за время E log V, но он может дать неверные результаты, если есть ребра с отрицательными весами.

---

Дополнительные сведения о реализации и связи версии 3 с алгоритмом Беллмана-Форда см. В этом ответе от zhihu. Это тоже мой ответ (но на китайском). Сейчас у меня нет времени переводить его на английский. Я очень признателен, если бы кто-то мог это сделать и отредактировать этот ответ в stackru.

Answer 4

Вы нигде не использовали S в своем алгоритме (помимо его изменения). идея dijkstra - это когда вершина находится на S, она никогда не будет изменена. в этом случае, как только B окажется внутри S, вы не достигнете его снова через C.

этот факт обеспечивает сложность O(E+VlogV) [в противном случае вы будете повторять ребра более одного раза, а вершины - более одного раза]

другими словами, алгоритм, который вы разместили, может быть не в O(E+VlogV), как обещал алгоритм Дейкстры.

Answer 5

Поскольку Dijkstra - это подход Greedy, после того, как вершина помечается как посещенная для этого цикла, она никогда не будет переоценена снова, даже если есть другой путь с меньшими затратами для его достижения в дальнейшем. И такая проблема может возникнуть только при наличии отрицательных ребер на графике.

---

Жадный алгоритм, как следует из названия, всегда делает выбор, который кажется лучшим в данный момент. Предположим, что у вас есть целевая функция, которую необходимо оптимизировать (максимизировать или минимизировать) в данной точке. Алгоритм Greedy делает жадный выбор на каждом этапе, чтобы обеспечить оптимизацию целевой функции. Алгоритм Жадности имеет только один выстрел для вычисления оптимального решения, чтобы он никогда не возвращался назад и не отменял решение.

Answer 6

Подумайте, что произойдет, если вы идете туда-сюда между B и C...

(актуально только если график не направлен)

Отредактировано: я полагаю, что проблема связана с тем фактом, что путь с AC * может быть только лучше, чем AB с наличием отрицательных весовых граней, поэтому не имеет значения, куда вы идете после AC, с предположением, что Отрицательные грани веса невозможно найти путь лучше, чем AB, если вы решили достичь B после перехода AC.

Answer 7

"2) Можем ли мы использовать алгоритм Дейксры для кратчайших путей для графов с отрицательными весами - одна идея может состоять в том, чтобы вычислить минимальное значение веса, добавить положительное значение (равное абсолютному значению минимального значения веса) ко всем весам и запустить алгоритм Дейксры. для модифицированного графа. Будет ли работать этот алгоритм?

Это абсолютно не работает, если все кратчайшие пути не имеют одинаковую длину. Например, для кратчайшего пути длиной два ребра и после добавления абсолютного значения к каждому ребру общая стоимость пути увеличивается на 2 * | максимальный отрицательный вес |. С другой стороны еще один путь длиной три ребра, поэтому стоимость пути увеличивается на 3 * | максимальный отрицательный вес |. Следовательно, все различные пути увеличиваются в разной степени.

Answer 8

Вы можете использовать алгоритм Дейкстры с отрицательными ребрами, не включая отрицательный цикл, но вы должны разрешить вершину посещать несколько раз, и эта версия потеряет свою быструю временную сложность.

В этом случае я практически видел, что лучше использовать алгоритм SPFA, который имеет нормальную очередь и может обрабатывать отрицательные края.

Answer 9

I will be just combining all the comments to give a better understanding of this problem.

There can be 2 ways of using Dijkstra's Algo :

1. Marking the nodes that have already found the minimum distance from the source (faster algo since we won't be revisiting nodes whose shortest path have been found already)

2. Not marking the nodes that have already found the minimum distance from the source (A bit slower than the above)

Now the doubt comes, what if we don't mark the nodes so that we can find shortest path including those containing negative weights ?

The ans is simple, consider a case when you only have only negative weights in the graph :

Consider the example in the picture(graph containing neg. cycle), now if you start from the node 0 (Source), you will have steps as(here I'm not marking the nodes) :

1. 0->0 as 0, 0->1 as inf , 0->2 as inf in the beginning

2. 0->1 as -1

3. 0->2 as -5

4. 0->0 as -8 (since we are not relaxing nodes)

5. 0->1 as -9 .. and so on

Since this loop will go forever therfore dijkstra's algo fails to find the minimum distance in case of negative weights (considering all the cases).