Дискретизированное непрерывное преобразование Фурье с нулем

Question

Рассмотрим функцию f(t), как мне вычислить непрерывное преобразование Фурье g (w) и построить его (используя numpy и matplotlib)?

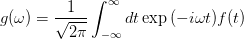
Эта или обратная задача (заданная g (w), график f (t) неизвестен) возникает, если не существует аналитического решения интеграла Фурье.

Answer 1

Вы можете использовать модуль FFT для этого, но вам придется проделать дополнительную работу. Сначала давайте посмотрим на интеграл Фурье и дискретизируем его: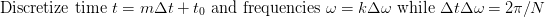Здесь k,m - целые числа, а N - число точек данных для f(t). Используя эту дискретизацию мы получаем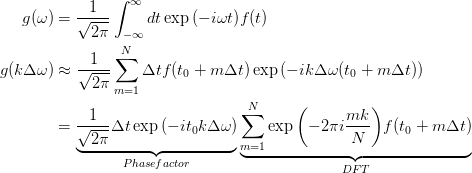

Сумма в последнем выражении - это в точности использование дискретных преобразований Фурье (ДПФ) (см. Раздел "Детали реализации" модуля "БПФ"). С этим знанием мы можем написать следующий скрипт на Python

import numpy as np
import matplotlib.pyplot as pl

#Consider function f(t)=1/(t^2+1)
#We want to compute the Fourier transform g(w)

#Discretize time t
t0=-100.
dt=0.001
t=np.arange(t0,-t0,dt)
#Define function
f=1./(t**2+1.)

#Compute Fourier transform by numpy's FFT function
g=np.fft.fft(f)
#frequency normalization factor is 2*np.pi/dt
w = np.fft.fftfreq(f.size)*2*np.pi/dt


#In order to get a discretisation of the continuous Fourier transform
#we need to multiply g by a phase factor
g*=dt*np.exp(-complex(0,1)*w*t0)/(np.sqrt(2*np.pi))

#Plot Result
pl.scatter(w,g,color="r")
#For comparison we plot the analytical solution
pl.plot(w,np.exp(-np.abs(w))*np.sqrt(np.pi/2),color="g")

pl.gca().set_xlim(-10,10)
pl.show()
pl.close()

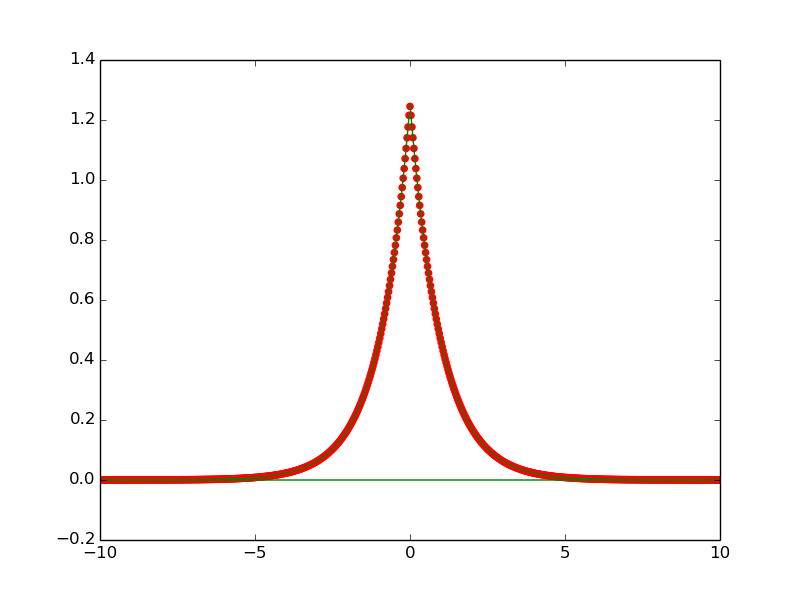
Полученный сюжет показывает, что скрипт работает