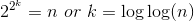Повторение T(n) = T(n^(1/2)) + 1
Я смотрел на это возвращение и хотел проверить, правильно ли я подходил.
T(n) = T(n^(1/2)) + 1
= T(n^(1/4)) + 1 + 1
= T(n^(1/8)) + 1 + 1 + 1
...
= 1 + 1 + 1 + ... + 1 (a total of rad n times)
= n^(1/2)
Таким образом, ответ пришел бы к тета-оценке п ^(1/2)
2 ответа
подсказка: предположим, что n = 22м или m = log2 log2 n, и вы знаете, что 22m-1 * 22m-1 = 22м, поэтому, если вы определите S (m) = T (n), то ваш S будет:
S (m) = S (m-1) +1 → S (m) = Θ(m) → S (m) = T (n) = Θ(log2 log2 n)
продлить его для общего случая.
В такой рекурсии, как T (n) = T (n / 2) + 1, вы уменьшите высоту дерева в 2 раза на каждой итерации, что приводит к Θ(logn), но в этом случае вы уменьшите входное число на степень двух (не два раза) так что будет Θ(log log n).
Вот как вы можете найти ответ без каких-либо подсказок, просто используя математику.
Начните раскручивать рекурсию: 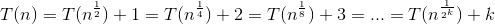 ,
,
В какой-то момент рекурсия остановится, поэтому мы должны найти разумную точку остановки. Пытаясь 0, 1, 2, вы можете видеть, что 2 выглядит хорошо, потому что вы можете легко решить уравнение: 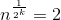 ,
,
Так что рекурсия продолжится log(log(n)) раз, и это ваше время сложность.
PS Немного сложнее было повторение здесь.