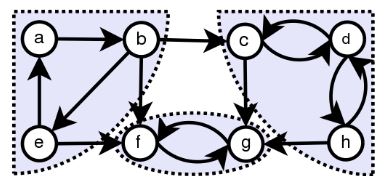
Итеративная DFS на графике с порядком после посещения
В настоящее время я пытаюсь реализовать алгоритм Косараю на ориентированном графе, чтобы найти все сильно связанные компоненты.
Я прекрасно понимаю, как работает этот алгоритм, но у меня есть некоторые проблемы при получении порядка DFS после посещения.
На данный момент псевдокод моей реализации DFS выглядит следующим образом:
[РЕДАКТИРОВАТЬ]: Я наконец-то получил версию DFS с порядком после посещения в качестве вывода. Я думал об увеличении числа, представляющего "блокировку" узла, каждый раз, когда этот узел помещает соседа в стек DFS. Затем, когда посещение узла заканчивается (больше нет соседей, чтобы подтолкнуть), я замечаю того, кто подтолкнул его, что DFS от этого дочернего элемента завершен (я уменьшаю его блокировку). Если это уведомление также завершает посещение предыдущего, я подхожу к предыдущему предыдущему узлу, чтобы заметить его и т. Д...
dfs(G, s):
for all v in vertices :
mark[v] = false
blocked[v] = 0
preceding[v] = -1
mark[s] = true
create a stack P
P.push(s)
while P not empty:
v = P.pop
for all t neighbours of v:
if mark[t] = false:
mark[t] = true
blocked[v]++
preceding[t] = v
P.push(t)
if no neighbours added to the stack:
while(blocked[v] == 0):
result.push(v);
v = (preceding[v] == -1) ? preceding[v] : v
blocked[v]--
Но я не уверен, что такого рода реализация выводит правильный почтовый порядок для алгоритма Косараджу.
Мой DFS прав или нет?
Пример моей DFS:
(Я перечислил вершины по часовой стрелке, поэтому a = 0, b = 1, c = 2, d = 3, h = 4, g = 5, f = 6, e = 7)
График как список смежности:
{0} -> {1}
{1} -> {2, 6, 7}
{2} -> {3, 5}
{3} -> {2, 4}
{4} -> {3, 5}
{5} -> {6}
{6} -> {5}
{7} -> {0, 6}
Другая проблема с моей DFS состоит в том, что мой алгоритм вычисляет соседей в порядке убывания. Я думал, что это не важно, потому что у соседей на самом деле множество вершин, но в моем примере у меня возникла странная проблема.
Объяснение возрастающего порядка вычисления соседей:
Ввод 0, открытие 1
Я извлекаю стек DFS (был {0}), он возвращает 0. Он имеет 1 в качестве соседа, поэтому я нажимаю 1 в стеке DFS (теперь это {1})
Ввод 1, открытие 2 6 7
Я извлекаю 1 из стека DFS, у него есть 2, 6 и 7 в качестве соседей, поэтому я помещаю их в стек (теперь это {7, 6, 2})
Ввод 2, открытие 3
Я извлекаю 2 из стека (теперь это {7, 6}), соседи 3 и 5, я нажимаю их, стек {7, 6, 5, 3}
Ввод 3, открытие 4
* Я извлекаю 3 из стека (теперь это {7, 6, 5}), 4 - единственный сосед, я нажимаю его, стек - {7, 6, 5, 4}
Ввод 4
Я вытаскиваю 4 из стека (это {7, 6, 5}), 5 - сосед, но уже "помечен", потому что был соседом 2
Ввод 5
Я вытолкнул 5 из стека, теперь {7, 6}, все соседи (6) уже "помечены"
Ввод 6
Я выталкиваю 6 из стека, {7}, 5 уже "помеченный" сосед
Ввод 7
Я вытаскиваю 7 из стека, {пусто}, соседи (1 и 6) уже "отмечены"
мой массив результатов равен 0 1 2 3 4 5 6 7, потому что я "обработал" узлы в этом порядке (или 7 6 5 4 3 2 1 0 с моей реализацией после посещения)
С уменьшением порядка вычисления соседей (мой фактический DFS) я получил:
Ввод 0, открытие 1
стек {} -> {1}
Ввод 1, открытие 7 6 2
стек {} -> {2, 6, 7}
Ввод 7
стек {2, 6} -> {2, 6}
Ввод 6, открытие 5
стек {2} -> {2, 5}
Ввод 5
стек {2} -> {2}
Ввод 2, открытие 3
стек {} -> {3}
Ввод 3, открытие 4
стек {} -> {4}
Ввод 4
stack {} -> {}
И я получил следующий результат 0 1 7 6 5 2 3 4 (или 4 3 2 5 6 7 1 0 для пост-посещения)
Проблема в том, что когда я переворачиваю график, чтобы вычислить заключительную часть алгоритма Косараджу, два результата не эквивалентны:
1-й результат (который в итоге дает правильное количество SCC) (стек {7, 6, 5, 4, 3, 2, 1, 0}):
При открытии 0 dfs возвращает 1 и 7 -> 0, 1, 7 находятся в одном и том же SCC, удаляют их из рабочего стека (теперь это {6, 5, 4, 3, 2}) и графика.
При открытии 2 dfs возвращает 3 и 4 -> 2, 3, 4 находятся в одном и том же SCC, удалите их из рабочего стека (теперь это {6, 5}) и графика.
Открытие 5, DFS возвращает 6 -> 5, 6 находятся в том же SCC
2n результат, стек {4, 3, 2, 5, 6, 7, 1, 0}:
При открытии 0 dfs возвращает 1 и 7 -> 0, 1, 7 находятся в одном и том же SCC, удаляют их из рабочего стека (теперь это {4, 3, 2, 5, 6}) и графика.
При открытии 6 dfs возвращает 5, 4, 3 и 2 -> 2, 3, 4, 5, 6 находятся в одном и том же SCC (НО ОНИ НЕ ПРОТИВ) (потому что в обратном графике, начиная с 6, я перехожу к 5, затем до 4 или 2...)
Может кто-нибудь объяснить мне, почему вычисление вершин в возрастающем или убывающем порядке в DFS не дает того же результата для алгоритма Косараджу?
РЕДАКТИРОВАТЬ: Я поместил некоторые дополнительные сведения о том, как я получаю результаты и как я запускаю алгоритм вручную. Надеюсь, теперь стало понятнее.
1 ответ
Вот моя C реализация DFS, получающая заказ после посещения, надеюсь, это будет кому-то полезно:
typedef struct _graph_list {
int nb_nodes;
int* tab_nodes;
int* succ_list;
} graph_list;
typedef struct _stack {
unsigned int max_capacity;
int* array;
int top_position;
} stack;
int* getSuccFromList(graph_list* graph, int i){
if (graph->tab_nodes[i] == -1) return NULL;
int case_succ = graph->tab_nodes[i];
int next_case_succ = graph->tab_nodes[++i];
while (next_case_succ == -1){
next_case_succ = graph->tab_nodes[++i];
}
int nb_succ = next_case_succ - case_succ;
int j;
int* res = malloc(sizeof(int)*(nb_succ + 1));
for(j = 0; j < nb_succ; j++){
res[j] = graph->succ_list[case_succ + j];
}
res[nb_succ] = -1;
return res;
}
int* dfsPostVisit(graph_list* graph, int vertex){
int i, j, nb_nodes, tmp_v;
int* succ;
int eof_visit;
nb_nodes = graph->nb_nodes;
int* res = malloc(sizeof(int)*(nb_nodes + 1));
int* mark = malloc(sizeof(int)*nb_nodes);
int* blocked = malloc(sizeof(int)*nb_nodes);
int* prec = malloc(sizeof(int)*nb_nodes);
for(i = 0; i < nb_nodes; i++){
res[i] = -1;
mark[i] = 0;
blocked[i] = 0;
prec[i] = -1;
}
res[nb_nodes] = -1;
stack* s = createStack(nb_nodes);
push(s, vertex);
mark[vertex] = 1;
i = 0;
while(!isEmpty(s)){
vertex = pop(s);
succ = getSuccFromList(graph, vertex);
j = 0;
eof_visit = 0;
if(succ!=NULL){
while(succ[j] != -1){
tmp_v = succ[j++];
if(!mark[tmp_v]){
mark[tmp_v] = 1;
blocked[vertex]++;
prec[tmp_v] = vertex;
push(s, tmp_v);
eof_visit++;
}
}
free(succ);
}
if (eof_visit == 0){
while (blocked[vertex] == 0){
res[i++] = vertex;
vertex = (prec[vertex] >= 0)? prec[vertex] : vertex;
blocked[vertex]--;
}
}
}
i = 0;
freeStack(s);
free(mark);
free(blocked);
free(prec);
return res;
}
Некоторые вещи могут нуждаться в улучшении, например, использование битовых массивов в качестве логических массивов вместо массивов int, но это мой реальный код, и похоже, что он работает.
Спасибо за тех, кто пытался мне помочь.