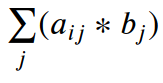Понимание Einsum NumPy
Я изо всех сил пытаюсь понять, как именно einsum работает. Я посмотрел на документацию и несколько примеров, но это не похоже на прилипание.
Вот пример, который мы рассмотрели в классе:
C = np.einsum("ij,jk->ki", A, B)
для двух массивовA а также B
Я думаю, что это займет A^T * B, но я не уверен (это принимает транспонирование одного из них, верно?). Может кто-нибудь рассказать мне, что именно здесь происходит (и вообще при использовании einsum)?
8 ответов
(Примечание: этот ответ основан на кратком сообщении в блоге о einsum Я написал некоторое время назад.)
Что значит einsum делать?
Представьте, что у нас есть два многомерных массива, A а также B, Теперь давайте предположим, что мы хотим...
- умножать
AсBопределенным образом создать новый массив продуктов; а потом возможно - суммируйте этот новый массив вдоль определенных осей; а потом возможно
- транспонировать оси нового массива в определенном порядке.
Есть хороший шанс, что einsum поможет нам сделать это быстрее и эффективнее с памятью, чем такие комбинации функций NumPy, как multiply, sum а также transpose позволит.
Как einsum Работа?
Вот простой (но не совсем тривиальный) пример. Возьмите следующие два массива:
A = np.array([0, 1, 2])
B = np.array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
Умножим A а также B поэлементно, а затем суммируйте по строкам нового массива. В "нормальном" NumPy мы написали бы:
>>> (A[:, np.newaxis] * B).sum(axis=1)
array([ 0, 22, 76])
Так вот, операция индексации на A выстраивает первые оси двух массивов так, чтобы умножение можно было транслировать. Строки массива продуктов затем суммируются, чтобы вернуть ответ.
Теперь, если мы хотим использовать einsum вместо этого мы могли бы написать:
>>> np.einsum('i,ij->i', A, B)
array([ 0, 22, 76])
Строка подписи 'i,ij->i' является ключом здесь и нуждается в небольшом объяснении. Вы можете думать об этом в две половины. С левой стороны (слева от ->) мы пометили два входных массива. Справа от ->, мы пометили массив, который мы хотим получить.
Вот что происходит дальше:
Aимеет одну ось; мы пометили этоi, А такжеBимеет две оси; мы пометили ось 0 какiи ось 1 какj,Повторяя ярлык
iв обоих входных массивах мы говоримeinsumчто эти две оси должны быть умножены вместе. Другими словами, мы умножаем массивAс каждым столбцом массиваB, какA[:, np.newaxis] * Bделает.Заметить, что
jне появляется в качестве метки в нашем желаемом выводе; мы только что использовалиi(мы хотим получить массив 1D). Опуская ярлык, мы говоримeinsumсуммировать по этой оси. Другими словами, мы суммируем строки продуктов, как.sum(axis=1)делает.
Это в основном все, что вам нужно знать, чтобы использовать einsum, Это помогает немного поиграть; если мы оставим обе метки в выводе, 'i,ij->ij'мы получаем двумерный массив продуктов (так же, как A[:, np.newaxis] * B). Если мы говорим, нет выходных меток, 'i,ij->мы вернем одно число (A[:, np.newaxis] * B).sum()).
Отличная вещь о einsum однако, это не создает временный массив продуктов в первую очередь; это просто суммирует продукты, как это идет. Это может привести к большой экономии в использовании памяти.
Немного больший пример
Чтобы объяснить скалярное произведение, вот два новых массива:
A = array([[1, 1, 1],
[2, 2, 2],
[5, 5, 5]])
B = array([[0, 1, 0],
[1, 1, 0],
[1, 1, 1]])
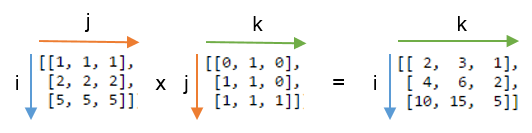
Мы вычислим скалярное произведение, используя np.einsum('ij,jk->ik', A, B), Вот картинка, показывающая маркировку A а также B и выходной массив, который мы получаем из функции:
Вы можете увидеть этот ярлык j повторяется - это означает, что мы умножаем строки A с колоннами B, Кроме того, этикетка j не входит в вывод - мы суммируем эти продукты. Этикетки i а также k сохраняются для вывода, поэтому мы возвращаем 2D-массив.
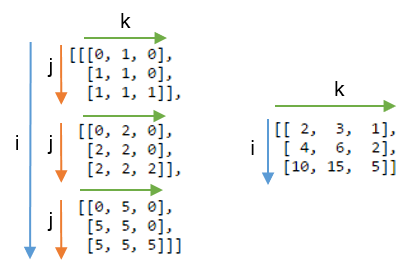
Может быть, еще яснее сравнить этот результат с массивом, в котором метка j не суммируется. Ниже, слева вы можете увидеть 3D-массив, полученный в результате записи np.einsum('ij,jk->ijk', A, B) (т.е. мы сохранили ярлык j):
Суммирующая ось j дает ожидаемое скалярное произведение, показанное справа.
Некоторые упражнения
Чтобы получить больше чувств для einsum, может быть полезно реализовать знакомые операции с массивом NumPy, используя нижнюю запись. Все, что включает в себя комбинации умножения и суммирования осей, может быть написано с использованием einsum,
Пусть A и B - два одномерных массива одинаковой длины. Например, A = np.arange(10) а также B = np.arange(5, 15),
Сумма
Aможно написать:np.einsum('i->', A)Поэлементное умножение,
A * B, можно написать:np.einsum('i,i->i', A, B)Внутренний продукт или точечный продукт,
np.inner(A, B)или жеnp.dot(A, B), можно написать:np.einsum('i,i->', A, B) # or just use 'i,i'Наружный продукт,
np.outer(A, B), можно написать:np.einsum('i,j->ij', A, B)
Для 2D-массивов C а также DПри условии, что оси имеют совместимую длину (обе имеют одинаковую длину или одну из них имеет длину 1), вот несколько примеров:
След
C(сумма главной диагонали),np.trace(C), можно написать:np.einsum('ii', C)Поэлементное умножение
Cи транспонированиеD,C * D.T, можно написать:np.einsum('ij,ji->ij', C, D)Умножая каждый элемент
Cпо массивуD(сделать 4D массив),C[:, :, None, None] * D, можно написать:np.einsum('ij,kl->ijkl', C, D)
Понимая идею numpy.einsum() это очень легко, если вы понимаете это интуитивно. В качестве примера приведем простое описание, включающее умножение матриц.
Использовать numpy.einsum() Вы должны передать в качестве аргумента так называемую строку индексов, а затем свои входные массивы.
Допустим, у вас есть два 2D-массива, A а также B и вы хотите сделать умножение матриц. Итак, вы делаете:
np.einsum("ij, jk -> ik", A, B)
Здесь нижняя строка ij соответствует массиву A в то время как нижняя строка jk соответствует массиву B, Кроме того, самое важное, что следует здесь отметить, это то, что количество символов в каждой строке индекса должно соответствовать размерам массива. (т.е. два символа для двумерных массивов, три символа для трехмерных массивов и т. д.) И если вы повторяете символы между строками нижнего индекса (j в нашем случае), то это означает, что вы хотите ein сумма произойдет по этим измерениям. Таким образом, они будут уменьшены. (то есть это измерение исчезнет)
Строка индекса после этого ->, будет наш результирующий массив. Если вы оставите это поле пустым, все будет суммировано, и в качестве результата будет возвращено скалярное значение. В противном случае результирующий массив будет иметь размеры в соответствии со строкой индекса. В нашем примере это будет ik, Это интуитивно понятно, потому что мы знаем, что для умножения матриц количество столбцов в массиве A должен соответствовать количеству строк в массиве B что здесь происходит (т.е. мы кодируем это знание, повторяя символ jв подстрочной строке)
Вот еще несколько примеров, иллюстрирующих использование np.einsum() в реализации некоторых общих тензорных или nd-массивных операций.
входные
# a vector
In [197]: vec
Out[197]: array([0, 1, 2, 3])
# an array
In [198]: A
Out[198]:
array([[11, 12, 13, 14],
[21, 22, 23, 24],
[31, 32, 33, 34],
[41, 42, 43, 44]])
# another array
In [199]: B
Out[199]:
array([[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3],
[4, 4, 4, 4]])
1) Матричное умножение (аналогично np.matmul(arr1, arr2))
In [200]: np.einsum("ij, jk -> ik", A, B)
Out[200]:
array([[130, 130, 130, 130],
[230, 230, 230, 230],
[330, 330, 330, 330],
[430, 430, 430, 430]])
2) Извлечь элементы по главной диагонали (аналогично np.diag(arr))
In [202]: np.einsum("ii -> i", A)
Out[202]: array([11, 22, 33, 44])
3) произведение Адамара (т.е. поэлементное произведение двух массивов) (аналогично arr1 * arr2)
In [203]: np.einsum("ij, ij -> ij", A, B)
Out[203]:
array([[ 11, 12, 13, 14],
[ 42, 44, 46, 48],
[ 93, 96, 99, 102],
[164, 168, 172, 176]])
4) Поэлементное возведение в квадрат (аналогично np.square(arr) или же arr ** 2)
In [210]: np.einsum("ij, ij -> ij", B, B)
Out[210]:
array([[ 1, 1, 1, 1],
[ 4, 4, 4, 4],
[ 9, 9, 9, 9],
[16, 16, 16, 16]])
5) Трассировка (т.е. сумма элементов главной диагонали) (аналогично np.trace(arr))
In [217]: np.einsum("ii -> ", A)
Out[217]: 110
6) Матрица транспонировать (аналогично np.transpose(arr))
In [221]: np.einsum("ij -> ji", A)
Out[221]:
array([[11, 21, 31, 41],
[12, 22, 32, 42],
[13, 23, 33, 43],
[14, 24, 34, 44]])
7) Наружное произведение (векторов) (аналогично np.outer(vec1, vec2))
In [255]: np.einsum("i, j -> ij", vec, vec)
Out[255]:
array([[0, 0, 0, 0],
[0, 1, 2, 3],
[0, 2, 4, 6],
[0, 3, 6, 9]])
8) Внутренний продукт (векторов) (аналогично np.inner(vec1, vec2))
In [256]: np.einsum("i, i -> ", vec, vec)
Out[256]: 14
9) Сумма по оси 0 (аналогично np.sum(arr, axis=0))
In [260]: np.einsum("ij -> j", B)
Out[260]: array([10, 10, 10, 10])
10) Сумма по оси 1 (аналогично np.sum(arr, axis=1))
In [261]: np.einsum("ij -> i", B)
Out[261]: array([ 4, 8, 12, 16])
11) Пакетное умножение матриц
In [287]: BM = np.stack((A, B), axis=0)
In [288]: BM
Out[288]:
array([[[11, 12, 13, 14],
[21, 22, 23, 24],
[31, 32, 33, 34],
[41, 42, 43, 44]],
[[ 1, 1, 1, 1],
[ 2, 2, 2, 2],
[ 3, 3, 3, 3],
[ 4, 4, 4, 4]]])
In [289]: BM.shape
Out[289]: (2, 4, 4)
# batch matrix multiply using einsum
In [292]: BMM = np.einsum("bij, bjk -> bik", BM, BM)
In [293]: BMM
Out[293]:
array([[[1350, 1400, 1450, 1500],
[2390, 2480, 2570, 2660],
[3430, 3560, 3690, 3820],
[4470, 4640, 4810, 4980]],
[[ 10, 10, 10, 10],
[ 20, 20, 20, 20],
[ 30, 30, 30, 30],
[ 40, 40, 40, 40]]])
In [294]: BMM.shape
Out[294]: (2, 4, 4)
12) Сумма по оси 2 (аналогично np.sum(arr, axis=2))
In [330]: np.einsum("ijk -> ij", BM)
Out[330]:
array([[ 50, 90, 130, 170],
[ 4, 8, 12, 16]])
13) Суммируйте все элементы в массиве (аналогично np.sum(arr))
In [335]: np.einsum("ijk -> ", BM)
Out[335]: 480
14) Сумма по нескольким осям (т.е. маргинализация)
(похожий на np.sum(arr, axis=(axis0, axis1, axis2, axis3, axis4, axis6, axis7)))
# 8D array
In [354]: R = np.random.standard_normal((3,5,4,6,8,2,7,9))
# marginalize out axis 5 (i.e. "n" here)
In [363]: esum = np.einsum("ijklmnop -> n", R)
# marginalize out axis 5 (i.e. sum over rest of the axes)
In [364]: nsum = np.sum(R, axis=(0,1,2,3,4,6,7))
In [365]: np.allclose(esum, nsum)
Out[365]: True
15) Продукты с двойными точками (аналог np.sum(hadamard-product), см. 3)
In [772]: A
Out[772]:
array([[1, 2, 3],
[4, 2, 2],
[2, 3, 4]])
In [773]: B
Out[773]:
array([[1, 4, 7],
[2, 5, 8],
[3, 6, 9]])
In [774]: np.einsum("ij, ij -> ", A, B)
Out[774]: 124
16) 2D и 3D умножение массива
Такое умножение может быть очень полезно при решении линейной системы уравнений (Ax = b), где вы хотите проверить результат.
# inputs
In [115]: A = np.random.rand(3,3)
In [116]: b = np.random.rand(3, 4, 5)
# solve for x
In [117]: x = np.linalg.solve(A, b.reshape(b.shape[0], -1)).reshape(b.shape)
# 2D and 3D array multiplication :)
In [118]: Ax = np.einsum('ij, jkl', A, x)
# indeed the same!
In [119]: np.allclose(Ax, b)
Out[119]: True
Наоборот, если нужно использовать np.matmul() для этой проверки мы должны сделать пару reshape Чтобы добиться этого, как:
# reshape 3D array `x` to 2D, perform matmul
# then reshape the resultant array to 3D
In [123]: Ax_matmul = np.matmul(A, x.reshape(x.shape[0], -1)).reshape(x.shape)
# indeed correct!
In [124]: np.allclose(Ax, Ax_matmul)
Out[124]: True
Бонус: Подробнее о математике здесь: Суммирование Эйнштейна и, безусловно, здесь: Тензорная запись
Читая уравнения эйнсума, я обнаружил, что наиболее полезным будет просто уметь мысленно свести их к их императивным версиям.
Начнем со следующего (внушительного) утверждения:
C = np.einsum('bhwi,bhwj->bij', A, B)
Сначала прорабатывая знаки препинания, мы видим, что у нас есть две капли, разделенные запятыми из 4 букв: bhwi а также bhwj, перед стрелкой и одной трехбуквенной каплей bijпосле этого. Следовательно, уравнение дает результат тензора ранга 3 из двух входных данных тензора ранга 4.
Теперь пусть каждая буква в каждом большом двоичном объекте будет именем переменной диапазона. Положение, в котором буква появляется в капле, является индексом оси, по которой она проходит в этом тензоре. Следовательно, императивное суммирование, производящее каждый элемент C, должно начинаться с трех вложенных циклов for, по одному для каждого индекса C.
for b in range(...):
for i in range(...):
for j in range(...):
# the variables b, i and j index C in the order of their appearance in the equation
C[b, i, j] = ...
Итак, по сути, у вас есть for цикл для каждого выходного индекса C. Мы пока оставим диапазоны неопределенными.
Затем мы посмотрим на левую часть - есть ли там какие-либо переменные диапазона, которые не отображаются в правой части? В нашем случае - да,h а также w. Добавить внутренний вложенныйfor цикл для каждой такой переменной:
for b in range(...):
for i in range(...):
for j in range(...):
C[b, i, j] = 0
for h in range(...):
for w in range(...):
...
Теперь внутри самого внутреннего цикла у нас есть все индексы, поэтому мы можем записать фактическое суммирование, и перевод завершен:
# three nested for-loops that index the elements of C
for b in range(...):
for i in range(...):
for j in range(...):
# prepare to sum
C[b, i, j] = 0
# two nested for-loops for the two indexes that don't appear on the right-hand side
for h in range(...):
for w in range(...):
# Sum! Compare the statement below with the original einsum formula
# 'bhwi,bhwj->bij'
C[b, i, j] += A[b, h, w, i] * B[b, h, w, j]
Если вы до сих пор могли следовать коду, поздравляем! Это все, что вам нужно для чтения уравнений эйнсума. Обратите внимание, в частности, на то, как исходная формула einsum преобразуется в окончательное суммирование в приведенном выше фрагменте. Циклы for и границы диапазона - пустяк, и этот последний оператор - все, что вам действительно нужно, чтобы понять, что происходит.
Для полноты картины давайте посмотрим, как определять диапазоны для каждой переменной диапазона. Что ж, диапазон каждой переменной - это просто длина индексируемых измерений. Очевидно, что если переменная индексирует более одного измерения в одном или нескольких тензорах, тогда длины каждого из этих измерений должны быть равны. Вот код выше с полными диапазонами:
# C's shape is determined by the shapes of the inputs
# b indexes both A and B, so its range can come from either A.shape or B.shape
# i indexes only A, so its range can only come from A.shape, the same is true for j and B
assert A.shape[0] == B.shape[0]
assert A.shape[1] == B.shape[1]
assert A.shape[2] == B.shape[2]
C = np.zeros((A.shape[0], A.shape[3], B.shape[3]))
for b in range(A.shape[0]): # b indexes both A and B, or B.shape[0], which must be the same
for i in range(A.shape[3]):
for j in range(B.shape[3]):
# h and w can come from either A or B
for h in range(A.shape[1]):
for w in range(A.shape[2]):
C[b, i, j] += A[b, h, w, i] * B[b, h, w, j]
Другой взгляд на
Большинство ответов здесь объясняются на примерах, я подумал, что выскажу дополнительную точку зрения.
- это универсальный инструмент для работы с матрицами. Данная строка содержит индексы, которые являются метками, представляющими оси. Мне нравится думать об этом как об определении вашей операции. Нижние индексы обеспечивают два очевидных ограничения:
количество осей для каждого входного массива,
равенство размеров оси между входами.
Возьмем начальный пример:. Здесь ограничения 1. переводятся в
A.ndim == 2 и
B.ndim == 2, и 2. к
A.shape[1] == B.shape[0].
Как вы увидите позже, есть и другие ограничения. Например:
метки в выходном нижнем индексе не должны появляться более одного раза.
метки в выходном нижнем индексе должны появиться во входных нижних индексах.
Глядя на это, вы можете думать об этом как о:
какие компоненты входных массивов будут способствовать компоненту
[k, i]выходного массива .
Индексы содержат точное определение операции для каждого компонента выходного массива.
Мы будем продолжать работу
ij,jk->ki, а также следующие определения и:
>>> A = np.array([[1,4,1,7], [8,1,2,2], [7,4,3,4]])
>>> A.shape
(3, 4)
>>> B = np.array([[2,5], [0,1], [5,7], [9,2]])
>>> B.shape
(4, 2)
Результат будет иметь форму
(B.shape[1], A.shape[0])и наивно могло быть построено следующим образом. Начиная с пустого массива для
Z:
Z = np.zeros((B.shape[1], A.shape[0]))
for i in range(A.shape[0]):
for j in range(A.shape[1]):
for k range(B.shape[0]):
Z[k, i] += A[i, j]*B[j, k] # ki <- ij*jk
о накоплении вкладов в выходной массив. Каждый
(A[i,j], B[j,k]) пара вносит свой вклад в каждый
Z[k, i] компонент.
Вы могли заметить, что это очень похоже на то, как вы будете вычислять общее умножение матриц ...
Минимальная реализация
Вот в некоторой степени минимальная реализация на Python. Некоторым это может помочь понять, что на самом деле происходит под капотом. Я считаю это таким же интуитивным, как и использование самого себя.
В дальнейшем я буду ссылаться на предыдущий пример. И определить
inputs в качестве
[A, B].
np.einsumна самом деле может принимать более двух входов! Далее мы сосредоточимся на общем случае: n входов и n входных индексов. Основная цель - найти область исследования, т.е. декартово произведение всех возможных диапазонов.
Мы не можем полагаться на ручное написание циклов просто потому, что не знаем, сколько нам понадобится! Основная идея такова: нам нужно найти все уникальные метки (я буду использовать
key и
keysчтобы ссылаться на них), найдите соответствующую форму массива, затем создайте диапазоны для каждого из них и вычислите произведение диапазонов, используя
Область изучения - декартово произведение:
range(0, 2) x range(0, 3) x range(0, 4).
Обработка индексов:
>>> expr = 'ij,jk->ki' >>> qry_expr, res_expr = expr.split('->') >>> inputs_expr = qry_expr.split(',') >>> inputs_expr, res_expr (['ij', 'jk'], 'ki')Найдите уникальные ключи ( метки ) во входных индексах:
>>> keys = set([(key, size) for keys, input in zip(inputs_expr, inputs) for key, size in list(zip(keys, input.shape))]) {('i', 3), ('j', 4), ('k', 2)}Мы должны проверять наличие ограничений (а также в выходном нижнем индексе)! С помощью
set- плохая идея, но она подойдет для целей этого примера.Нам понадобится список, содержащий ключи ( метки ):
>>> to_key = [key for key, _ in keys] ['k', 'i', 'j']Получите связанные размеры (используемые для инициализации выходного массива) и создайте диапазоны (используемые для создания нашей области итерации):
>>> sizes = {key: size for key, size in keys} {'i': 3, 'j': 4, 'k': 2} >>> ranges = [range(size) for _, size in keys] [range(0, 2), range(0, 3), range(0, 4)]Вычислить декартово произведение
ranges>>> domain = product(*ranges)Остерегайтесь :
itertools.productвозвращает итератор, который со временем расходуется .Инициализируйте выходной тензор как:
>>> res = np.zeros([sizes[key] for key in res_expr])Мы будем зацикливаться
domain:>>> for indices in domain: ... passДля каждой итерации будет содержать значения по каждой оси. В нашем примере это значения, и как кортеж :
(k, i, j). Как будто мы были внутри трехforпетли. Для каждого входа (AиB) нам нужно определить, какой компонент выбрать. ЭтоA[i, j]иB[j, k], да! Но это не поможет, потому что у нас нет переменныхi,j, иk(буквально).Мы можем застегнуть
indicesсto_keyчтобы создать соответствие между каждым ключом ( меткой ) и его текущим значением:>>> vals= {k: v for v, k in zip(indices, to_key)}Чтобы получить координаты для выходного массива, мы используем
valsи перебрать ключи:[vals[key] for key in res_expr]. Однако, чтобы использовать их для индексации выходного массива, нам нужно обернуть егоtupleиzipдля разделения индексов по каждой оси:>>> res_ind = tuple(zip([vals[key] for key in res_expr]))То же и для входных индексов (хотя их может быть несколько):
>>> inputs_ind = [tuple(zip([vals[key] for key in expr])) for expr in inputs_expr]Мы будем использовать
itertools.reduce
>>> def reduce_mult(L):
... return reduce(lambda x, y: x*y, L)
В целом цикл по домену выглядит так:
>>> for indices in domain:
... vals = {k: v for v, k in zip(indices, to_key)}
... res_ind = tuple(zip([vals[key] for key in res_expr]))
... inputs_ind = [tuple(zip([vals[key] for key in expr]))
... for expr in inputs_expr]
...
... res[res_ind] += reduce_mult([M[i] for M, i in zip(inputs, inputs_ind)])
>>> res
array([[70., 44., 65.],
[30., 59., 68.]])
* Уф * , это довольно близко к
np.einsum('ij,jk->ki', A, B)!
Я нашел NumPy: хитрости торговли (Часть II) поучительными
Мы используем ->, чтобы указать порядок выходного массива. Так что думайте о "ij, i->j" как о левой стороне (LHS) и правой стороне (RHS). Любое повторение меток на LHS вычисляет элемент продукта, а затем суммирует. Изменяя метку на стороне RHS (выходной), мы можем определить ось, по которой мы хотим перейти относительно входного массива, то есть суммирование по оси 0, 1 и так далее.
import numpy as np
>>> a
array([[1, 1, 1],
[2, 2, 2],
[3, 3, 3]])
>>> b
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
>>> d = np.einsum('ij, jk->ki', a, b)
Обратите внимание, что есть три оси, i, j, k, и это j повторяется (слева). i,j представлять строки и столбцы для a, j,k за b,
Для того, чтобы рассчитать продукт и выровнять j ось нам нужно добавить ось a, (b будет транслироваться вдоль (?) первой оси)
a[i, j, k]
b[j, k]
>>> c = a[:,:,np.newaxis] * b
>>> c
array([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 0, 2, 4],
[ 6, 8, 10],
[12, 14, 16]],
[[ 0, 3, 6],
[ 9, 12, 15],
[18, 21, 24]]])
j отсутствует с правой стороны, поэтому мы суммируем j которая является второй осью массива 3x3x3
>>> c = c.sum(1)
>>> c
array([[ 9, 12, 15],
[18, 24, 30],
[27, 36, 45]])
Наконец, индексы (в алфавитном порядке) обращены справа, поэтому мы транспонируем.
>>> c.T
array([[ 9, 18, 27],
[12, 24, 36],
[15, 30, 45]])
>>> np.einsum('ij, jk->ki', a, b)
array([[ 9, 18, 27],
[12, 24, 36],
[15, 30, 45]])
>>>
Давайте сделаем 2 массива с разными, но совместимыми размерами, чтобы подчеркнуть их взаимодействие
In [43]: A=np.arange(6).reshape(2,3)
Out[43]:
array([[0, 1, 2],
[3, 4, 5]])
In [44]: B=np.arange(12).reshape(3,4)
Out[44]:
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
Ваш расчет принимает "точку" (сумму произведений) от (2,3) с (3,4) для получения массива (4,2). i 1-й тусклый Aпоследний из C; k последний из B1-й из C, j "потребляется" суммированием.
In [45]: C=np.einsum('ij,jk->ki',A,B)
Out[45]:
array([[20, 56],
[23, 68],
[26, 80],
[29, 92]])
Это так же, как np.dot(A,B).T - это конечный результат, который транспонирован.
Чтобы увидеть больше того, что происходит с j, изменить C подписки на ijk:
In [46]: np.einsum('ij,jk->ijk',A,B)
Out[46]:
array([[[ 0, 0, 0, 0],
[ 4, 5, 6, 7],
[16, 18, 20, 22]],
[[ 0, 3, 6, 9],
[16, 20, 24, 28],
[40, 45, 50, 55]]])
Это также может быть произведено с:
A[:,:,None]*B[None,:,:]
То есть добавить k измерение до конца Aи i перед B, в результате чего (2,3,4) массив.
0 + 4 + 16 = 20, 9 + 28 + 55 = 92, так далее; Сумма на j и транспонировать, чтобы получить более ранний результат:
np.sum(A[:,:,None] * B[None,:,:], axis=1).T
# C[k,i] = sum(j) A[i,j (,k) ] * B[(i,) j,k]
После знакомства с фиктивным индексом (общим или повторяющимся индексом) и суммированием по фиктивному индексу в суммировании Эйнштейна (einsum) формирование выходных данных становится простым. Следовательно, сосредоточьтесь на:
- Фиктивный индекс, общий индекс в
np.einsum("ij,jk->ki", a, b) - Суммирование по фиктивному индексу
Фиктивный индекс
За
einsum("...", a, b), поэлементное умножение всегда происходит между матрицами, независимо от того, есть ли общие индексы или нет. Мы можем иметь
einsum('xy,wz', a, b) у которого нет общего индекса в нижних индексах
'xy,wz'.
Если есть общий индекс, как в
"ij,jk->ki", то в суммировании Эйнштейна он называется фиктивным индексом .
Суммируемый индекс является индексом суммирования, в данном случае «i». Его также называют фиктивным индексом, поскольку любой символ может заменить «i» без изменения значения выражения при условии, что он не конфликтует с индексными символами в том же термине.
Суммирование по фиктивному индексу
За
np.einsum("ij,j", a, b)из зеленого прямоугольника на диаграмме, является индексом фиктивного. Поэлементное умножение
a[i][j] * b[j] суммируется по
j ось как
Σ ( a[i][j] * b[j] ).
Это точечный продукт
np.inner(a[i], b)для каждого . Здесь конкретно с
np.inner() и избегая
np.dotпоскольку это не строго математическая операция скалярного произведения .
Фиктивный индекс может появляться где угодно, если соблюдаются правила (подробности см. На YouTube).
Для фиктивного индекса в
np.einsum(“ik,il", a, b), это индекс строки матриц и, следовательно, столбцы из и из извлекаются для генерации скалярного произведения s.
Форма вывода
Поскольку суммирование происходит по фиктивному индексу , фиктивный индекс исчезает в матрице результатов, следовательно,
i из
“ik,il" опускается и формирует форму
(k,l). Мы можем сказать
np.einsum("... -> <shape>")чтобы указать форму вывода с помощью меток нижнего индекса вывода с
-> идентификатор.
Подробнее см. Явный режим в numpy.einsum .
В явном режиме выводом можно напрямую управлять, задав метки нижнего индекса вывода. Для этого требуется идентификатор
‘->’а также список меток выходных индексов. Эта функция увеличивает гибкость функции, так как при необходимости суммирование можно отключить или принудительно. Звонокnp.einsum('i->', a)какnp.sum(a, axis=-1), иnp.einsum('ii->i', a)какnp.diag(a). Разница в том, что по умолчанию einsum не разрешает трансляцию. Кроме тогоnp.einsum('ij,jh->ih', a, b)напрямую определяет порядок меток выходных нижних индексов и, следовательно, возвращает матричное умножение, в отличие от приведенного выше примера в неявном режиме.
Без фиктивного индекса
Пример отсутствия фиктивного индекса в einsum.
- Термин (индексы нижнего индекса, например
"ij") выбирает элемент в каждом массиве. - Каждый элемент с левой стороны применяется к элементу с правой стороны для поэлементного умножения (следовательно, умножение всегда происходит).
a имеет форму (2,3), каждый элемент которой нанесен на
bформы (2,2). Следовательно, он создает матрицу формы
(2,3,2,2) без суммирования как
(i,j),
(k.l) все индексы бесплатные.
# --------------------------------------------------------------------------------
# For np.einsum("ij,kl", a, b)
# 1-1: Term "ij" or (i,j), two free indices, selects selects an element a[i][j].
# 1-2: Term "kl" or (k,l), two free indices, selects selects an element b[k][l].
# 2: Each a[i][j] is applied on b[k][l] for element-wise multiplication a[i][j] * b[k,l]
# --------------------------------------------------------------------------------
# for (i,j) in a:
# for(k,l) in b:
# a[i][j] * b[k][l]
np.einsum("ij,kl", a, b)
array([[[[ 0, 0],
[ 0, 0]],
[[10, 11],
[12, 13]],
[[20, 22],
[24, 26]]],
[[[30, 33],
[36, 39]],
[[40, 44],
[48, 52]],
[[50, 55],
[60, 65]]]])
Я думаю, что самый простой пример - в документации по тензорному потоку
Есть четыре шага для преобразования вашего уравнения в нотацию einsum. Давайте возьмем это уравнение в качестве примераC[i,k] = sum_j A[i,j] * B[j,k]
- Сначала мы отбрасываем имена переменных. Мы получили
ik = sum_j ij * jk - Мы бросаем
sum_jтермин как неявный. Мы получилиik = ij * jk - Мы заменяем
*с,. Мы получилиik = ij, jk - Вывод находится на правой стороне и разделен
->подписать. Мы получилиij, jk -> ik
Интерпретатор einsum просто выполняет эти 4 шага в обратном порядке. Все показатели, отсутствующие в результате, суммируются.
Вот еще несколько примеров из документации
# Matrix multiplication
einsum('ij,jk->ik', m0, m1) # output[i,k] = sum_j m0[i,j] * m1[j, k]
# Dot product
einsum('i,i->', u, v) # output = sum_i u[i]*v[i]
# Outer product
einsum('i,j->ij', u, v) # output[i,j] = u[i]*v[j]
# Transpose
einsum('ij->ji', m) # output[j,i] = m[i,j]
# Trace
einsum('ii', m) # output[j,i] = trace(m) = sum_i m[i, i]
# Batch matrix multiplication
einsum('aij,ajk->aik', s, t) # out[a,i,k] = sum_j s[a,i,j] * t[a, j, k]