Форма PCA .fit_transform Scikit-learn является несовместимой (n_samples << m_attributes)
Я получаю разные формы для моего PCA, используя sklearn, Почему мое преобразование не приводит к массиву тех же размеров, что и документы?
fit_transform(X, y=None)
Fit the model with X and apply the dimensionality reduction on X.
Parameters:
X : array-like, shape (n_samples, n_features)
Training data, where n_samples is the number of samples and n_features is the number of features.
Returns:
X_new : array-like, shape (n_samples, n_components)
Проверьте это с помощью набора данных iris, который (150, 4) где я делаю 4 ПК:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn import decomposition
import seaborn as sns; sns.set_style("whitegrid", {'axes.grid' : False})
%matplotlib inline
np.random.seed(0)
# Iris dataset
DF_data = pd.DataFrame(load_iris().data,
index = ["iris_%d" % i for i in range(load_iris().data.shape[0])],
columns = load_iris().feature_names)
Se_targets = pd.Series(load_iris().target,
index = ["iris_%d" % i for i in range(load_iris().data.shape[0])],
name = "Species")
# Scaling mean = 0, var = 1
DF_standard = pd.DataFrame(StandardScaler().fit_transform(DF_data),
index = DF_data.index,
columns = DF_data.columns)
# Sklearn for Principal Componenet Analysis
# Dims
m = DF_standard.shape[1]
K = m
# PCA (How I tend to set it up)
M_PCA = decomposition.PCA()
A_components = M_PCA.fit_transform(DF_standard)
#DF_standard.shape, A_components.shape
#((150, 4), (150, 4))
но потом, когда я использую тот же точный подход к моему фактическому набору данных (76, 1989) как в 76 samples а также 1989 attributes/dimensions Я получаю (76, 76) массив вместо (76, 1989)
DF_centered = normalize(DF_mydata, method="center", axis=0)
m = DF_centered.shape[1]
# print(m)
# 1989
M_PCA = decomposition.PCA(n_components=m)
A_components = M_PCA.fit_transform(DF_centered)
DF_centered.shape, A_components.shape
# ((76, 1989), (76, 76))
normalize это просто оболочка, которую я сделал, что вычитает mean из каждого измерения.
1 ответ
(Примечание: этот ответ адаптирован из моего ответа о перекрестной проверке здесь: почему существует только n−1 главных компонентов для n точек данных, если число измерений больше или равно n?)
PCA (как обычно выполняется) создает новую систему координат путем:
- смещение источника в центр тяжести ваших данных,
- сжимает и / или растягивает оси, чтобы сделать их равными по длине, и
- поворачивает ваши оси в новую ориентацию.
(Для получения дополнительной информации см. Эту превосходную ветку CV: Имеет смысл анализа главных компонентов, собственных векторов и собственных значений.) Однако, шаг 3 вращает ваши оси особым образом. Ваш новый X1 (теперь называется "PC1", т. Е. Первый основной компонент) ориентирован в направлении максимальных вариаций ваших данных. Второй главный компонент ориентирован в направлении следующего наибольшего количества вариаций, которое ортогонально первому главному компоненту. Остальные основные компоненты формируются аналогичным образом.
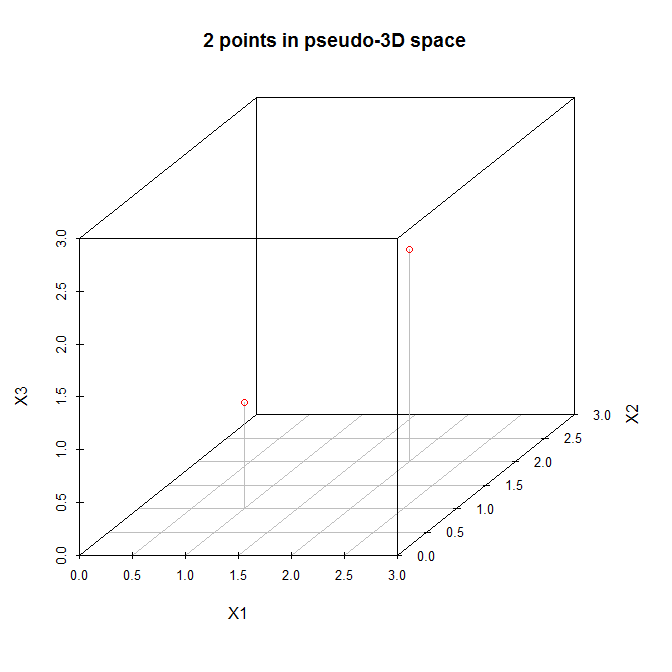
Имея это в виду, давайте рассмотрим простой пример (предложенный @amoeba в комментарии). Вот матрица данных с двумя точками в трехмерном пространстве:
X = [ 1 1 1
2 2 2 ]
Давайте рассмотрим эти точки на (псевдо) трехмерном графике рассеяния:
Итак, давайте следовать шагам, перечисленным выше. (1) Источник новой системы координат будет расположен в (1.5,1.5,1.5). (2) Оси уже равны. (3) Первый главный компонент будет идти по диагонали от того, что было (0,0,0) к тому, что было изначально (3,3,3), что является направлением наибольшего отклонения для этих данных. Теперь второй главный компонент должен быть ортогональным к первому и должен идти в направлении наибольшего оставшегося отклонения. Но какое это направление? Это от (0,0,3) до (3,3,0) или от (0,3,0) до (3,0,3) или что-то еще? Не существует оставшихся изменений, поэтому не может быть больше основных компонентов.
С N=2 данными мы можем соответствовать (не более) N−1=1 основным компонентам.