Найти максимальную выпуклую площадь

Question

Мой вопрос очень похож на вопрос Плуга; но с этой разницей:

Как найти максимальную выпуклую область, которая может поместиться в невыпуклой области?

Для примера рассмотрим эту невыпуклую область:

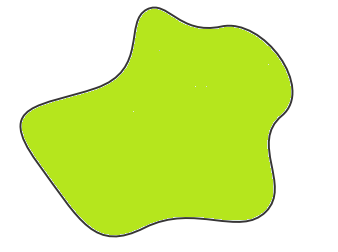
Любые идеи или решения будут оценены, спасибо.

Answer 1

Я написал ответ на этот вопрос на Математическом обмене стеками и включил изображение, которое я создал, используя реализацию концепции. Подход, используемый для этого, может работать для многих практических приложений, поэтому я опишу его здесь более подробно.

Возьмите свою форму и приблизьте ее, используя многоугольник. Определите трассы последовательных вершин, у которых внутренний угол> 180°. Для каждого такого прогона повторяйте все возможные касательные линии. Касательная к трассе - это линия, соединяющая две последовательные вершины, по крайней мере, одна из которых находится внутри трассы. Это означает, что первая строка определяется последней вершиной перед прогоном и первой вершиной прогона. Возьмите направленную внутрь полуплоскость, определенную этой линией, и пересекайте ее с вашей формой, затем вычислите площадь и сравните ее с лучшим решением, найденным до сих пор.

В упрощенном подходе вы просто создали бы рекурсивную схему, чтобы опробовать все возможные комбинации линий. это означает временную сложность O (n^m), где n - количество вершин, а m - количество прогонов. В более сложном подходе вы могли бы использовать тот факт, что линия, которая не пересекает любую другую линию внутри фигуры, может быть выбрана независимо от этих других. То же самое верно для групп линий, которые не пересекаются друг с другом внутри фигуры. Некоторые варианты выбора будут полностью исключать другой маршрут, так что выбор, сделанный для этого цикла, станет неактуальным. Таким образом, здесь есть большой потенциал для умных алгоритмов, в зависимости от того, сколько усилий вы можете инвестировать и какую производительность вам требуется.

Если ваш ввод является многоугольником, то линия, касающаяся невыпуклой вершины, не обязательно должна совпадать ни с входным, ни с исходящим ребром многоугольника, а может произвольно поворачиваться между этими двумя пределами. Для этого случая вышеуказанный подход может дать неоптимальное решение. Но так как вы заявили в комментарии, что мы можем принимать "неполигональные" формы, которые я понимаю как "гладкие". В этом случае у вас есть четко определенный касательный в каждой точке, и каждый касательный будет достаточно близко к краю многоугольного приближения.

Вопреки тому, что я изначально считал, вышеприведенное должно работать и для фигур с отверстиями, поскольку граница выпуклого отверстия приведет к невыпуклому прогону самой фигуры. Таким образом, этот запуск гарантирует, что вы исследуете все возможные способы вырезать дыру. SImilar для невыпуклых отверстий: соответствующие прогоны гарантируют, что вы также вырезаете их, не теряя выпуклых решений.

Применительно к вашему примеру изображения алгоритм дает следующий результат:

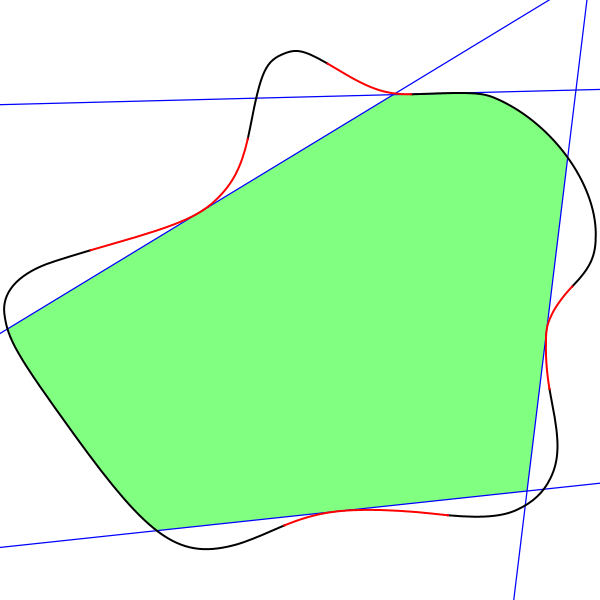
Невыпуклые участки вершин окрашены в красный цвет, лучший набор линий - в синий, а результирующая область - в зеленый. Многоугольник позади этого имеет 269 вершин. Реализация была сделана в Java, с небольшим учетом производительности, рекурсивным поиском всех возможных комбинаций методом грубой силы и некоторыми допущениями, которые работают для этих входных данных, но могут вообще потерпеть неудачу.