Почему умножение матриц быстрее в numpy, чем в ctypes в Python?
Я пытался найти самый быстрый способ умножения матриц и пробовал 3 разных способа:
- Чистая реализация на python: здесь нет сюрпризов.
- Numpy реализация с использованием
numpy.dot(a, b) - Взаимодействие с C с помощью
ctypesмодуль в Python.
Это код C, который преобразуется в общую библиотеку:
#include <stdio.h>
#include <stdlib.h>
void matmult(float* a, float* b, float* c, int n) {
int i = 0;
int j = 0;
int k = 0;
/*float* c = malloc(nay * sizeof(float));*/
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
int sub = 0;
for (k = 0; k < n; k++) {
sub = sub + a[i * n + k] * b[k * n + j];
}
c[i * n + j] = sub;
}
}
return ;
}
И код Python, который вызывает его:
def C_mat_mult(a, b):
libmatmult = ctypes.CDLL("./matmult.so")
dima = len(a) * len(a)
dimb = len(b) * len(b)
array_a = ctypes.c_float * dima
array_b = ctypes.c_float * dimb
array_c = ctypes.c_float * dima
suma = array_a()
sumb = array_b()
sumc = array_c()
inda = 0
for i in range(0, len(a)):
for j in range(0, len(a[i])):
suma[inda] = a[i][j]
inda = inda + 1
indb = 0
for i in range(0, len(b)):
for j in range(0, len(b[i])):
sumb[indb] = b[i][j]
indb = indb + 1
libmatmult.matmult(ctypes.byref(suma), ctypes.byref(sumb), ctypes.byref(sumc), 2);
res = numpy.zeros([len(a), len(a)])
indc = 0
for i in range(0, len(sumc)):
res[indc][i % len(a)] = sumc[i]
if i % len(a) == len(a) - 1:
indc = indc + 1
return res
Я бы поспорил, что версия с использованием C была бы быстрее... и я бы проиграл! Ниже мой тест, который, кажется, показывает, что я либо сделал это неправильно, или что numpy тупо быстро
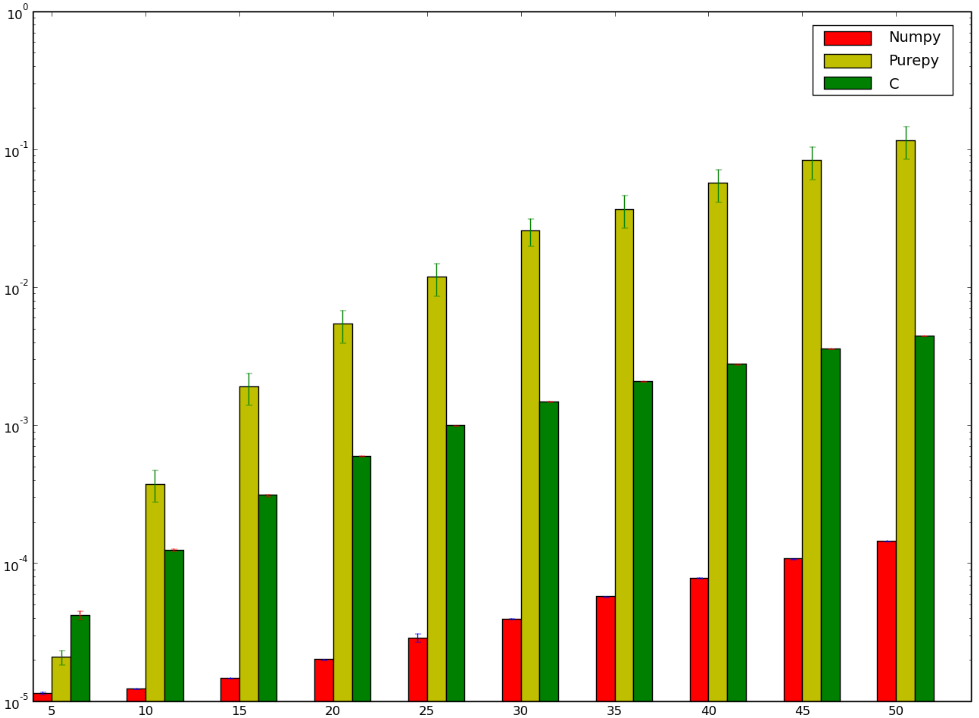
Я хотел бы понять, почему numpy версия быстрее, чем ctypes версия, я даже не говорю о чистой реализации Python, так как это отчасти очевидно.
7 ответов
Я не слишком знаком с Numpy, но источник на Github. Часть точечных продуктов реализована в https://github.com/numpy/numpy/blob/master/numpy/core/src/multiarray/arraytypes.c.src, который, как я предполагаю, переводится в конкретные реализации C для каждого тип данных. Например:
/**begin repeat
*
* #name = BYTE, UBYTE, SHORT, USHORT, INT, UINT,
* LONG, ULONG, LONGLONG, ULONGLONG,
* FLOAT, DOUBLE, LONGDOUBLE,
* DATETIME, TIMEDELTA#
* #type = npy_byte, npy_ubyte, npy_short, npy_ushort, npy_int, npy_uint,
* npy_long, npy_ulong, npy_longlong, npy_ulonglong,
* npy_float, npy_double, npy_longdouble,
* npy_datetime, npy_timedelta#
* #out = npy_long, npy_ulong, npy_long, npy_ulong, npy_long, npy_ulong,
* npy_long, npy_ulong, npy_longlong, npy_ulonglong,
* npy_float, npy_double, npy_longdouble,
* npy_datetime, npy_timedelta#
*/
static void
@name@_dot(char *ip1, npy_intp is1, char *ip2, npy_intp is2, char *op, npy_intp n,
void *NPY_UNUSED(ignore))
{
@out@ tmp = (@out@)0;
npy_intp i;
for (i = 0; i < n; i++, ip1 += is1, ip2 += is2) {
tmp += (@out@)(*((@type@ *)ip1)) *
(@out@)(*((@type@ *)ip2));
}
*((@type@ *)op) = (@type@) tmp;
}
/**end repeat**/
Похоже, что это для вычисления одномерных точечных произведений, то есть по векторам. За несколько минут просмотра Github я не смог найти источник для матриц, но возможно, что он использует один вызов FLOAT_dot для каждого элемента в матрице результатов. Это означает, что цикл в этой функции соответствует вашему внутреннему циклу.
Одно из различий между ними заключается в том, что "шаг" - разница между последовательными элементами во входных данных - явно вычисляется один раз перед вызовом функции. В вашем случае нет шага, и смещение каждого входа вычисляется каждый раз, например a[i * n + k], Я бы ожидал, что хороший компилятор оптимизирует это до чего-то похожего на шаг Numpy, но, возможно, он не сможет доказать, что шаг является постоянным (или он не оптимизируется).
Numpy также может делать что-то умное с эффектами кэша в коде более высокого уровня, который вызывает эту функцию. Обычный трюк - подумать о том, является ли каждая строка смежной, или о каждом столбце, - и сначала попытаться перебрать каждую смежную часть. Кажется трудным быть совершенно оптимальным, для каждого точечного произведения одна входная матрица должна пересекаться строками, а другая - столбцами (если только они не были сохранены в другом главном порядке). Но это может, по крайней мере, сделать это для элементов результата.
Numpy также содержит код для выбора реализации определенных операций, включая "точку", из разных базовых реализаций. Например, он может использовать библиотеку BLAS. Из приведенного выше обсуждения звучит так, как будто используется CBLAS. Это было переведено с Fortran на C. Я думаю, что реализация, используемая в вашем тесте, будет найдена здесь: http://www.netlib.org/clapack/cblas/sdot.c.
Обратите внимание, что эта программа была написана машиной для чтения другой машиной. Но вы можете увидеть внизу, что он использует развернутый цикл для обработки 5 элементов одновременно:
for (i = mp1; i <= *n; i += 5) {
stemp = stemp + SX(i) * SY(i) + SX(i + 1) * SY(i + 1) + SX(i + 2) *
SY(i + 2) + SX(i + 3) * SY(i + 3) + SX(i + 4) * SY(i + 4);
}
Этот фактор развертывания, вероятно, был выбран после профилирования нескольких. Но одно теоретическое преимущество заключается в том, что между каждой точкой ветвления выполняется больше арифметических операций, и у компилятора и ЦП есть больше выбора относительно того, как оптимально планировать их, чтобы получить как можно больше конвейерной обработки команд.
NumPy использует высокооптимизированный, тщательно настроенный метод BLAS для умножения матриц (см. Также: ATLAS). Специфической функцией в этом случае является GEMM (для общего умножения матриц). Вы можете посмотреть оригинал, выполнив поиск dgemm.f (это в Netlib).
Кстати, оптимизация выходит за рамки оптимизации компилятора. Выше Филипп упомянул Копперсмит-Виноград. Если я правильно помню, это алгоритм, который используется для большинства случаев умножения матриц в ATLAS (хотя комментатор отмечает, что это может быть алгоритм Штрассена).
Другими словами, ваш matmult Алгоритм является тривиальной реализацией. Есть более быстрые способы сделать то же самое.
Язык, используемый для реализации определенной функциональности, сам по себе является плохой мерой производительности. Часто использование более подходящего алгоритма является решающим фактором.
В вашем случае вы используете наивный подход к умножению матриц, как преподается в школе, который находится в O(n^3). Тем не менее, вы можете сделать намного лучше для определенных видов матриц, например, квадратные матрицы, запасные матрицы и так далее.
Взгляните на алгоритм Копперсмита – Винограда (умножение квадратной матрицы в O(n^2.3737)), чтобы получить хорошую отправную точку для быстрого умножения матриц. Также см. Раздел "Ссылки", в котором перечислены некоторые ссылки на еще более быстрые методы.
Для более естественного примера удивительного прироста производительности, попробуйте написать быстрый strlen() и сравните это с реализацией glibc. Если вам не удается победить, прочитайте glibc strlen() Источник, он имеет довольно хорошие комментарии.
Парни, которые написали NumPy, очевидно, знают, что они делают.
Есть много способов оптимизировать матричное умножение. Например, порядок обхода матрицы влияет на шаблоны доступа к памяти, которые влияют на производительность.
Хорошее использование SSE - это еще один способ оптимизации, который, вероятно, использует NumPy.
Могут быть и другие способы, о которых разработчики NumPy знают, а я нет.
Кстати, вы скомпилировали свой код C с optiomization?
Вы можете попробовать следующую оптимизацию для C. Она работает параллельно, и я предполагаю, что NumPy делает что-то в том же духе.
ПРИМЕЧАНИЕ: работает только для четных размеров. С помощью дополнительной работы вы можете снять это ограничение и сохранить улучшение производительности.
for (i = 0; i < n; i++) {
for (j = 0; j < n; j+=2) {
int sub1 = 0, sub2 = 0;
for (k = 0; k < n; k++) {
sub1 = sub1 + a[i * n + k] * b[k * n + j];
sub1 = sub1 + a[i * n + k] * b[k * n + j + 1];
}
c[i * n + j] = sub;
c[i * n + j + 1] = sub;
}
}
}
Numpy также высоко оптимизированный код. Эссе о его части есть в книге " Красивый код".
Ctypes должен пройти динамический перевод с C на Python и обратно, что добавляет некоторые накладные расходы. В Numpy большинство матричных операций выполняются полностью внутренне.
Наиболее распространенная причина, по которой преимущество Fortran в числовом коде заключается в том, что язык облегчает обнаружение псевдонимов - компилятор может сказать, что умножаемые матрицы не используют одну и ту же память, что может помочь улучшить кеширование (нет необходимо убедиться, что результаты немедленно записываются обратно в "общую" память). Именно поэтому в C99 введены ограничения.
Тем не менее, в этом случае, мне интересно, умудряется ли также код numpy использовать некоторые специальные инструкции, которых нет в коде C (так как разница кажется особенно большой).
Недавняя статья установила самый быстрый рекорд по умножению двух матриц. Но это также знаменует собой конец линии для метода, на который исследователи полагались на протяжении десятилетий для улучшения.
https://www.quantamagazine.org/mathematicians-inch-closer-to-matrix-multiplication-goal-20210323/