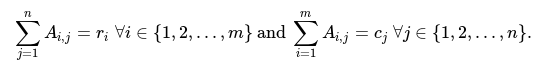Рекурсивный алгоритм не может завершить тесты за отведенное время

Question

Рекурсивный алгоритм не может завершить тесты за отведенное время

Я делал тест, который требовал алгоритма бинарной томографии. Поставляется набор из 38 тестовых значений, которые проверяют правильность теста, но есть также ограничение по времени в 1 ЦП для завершения всех тестов. Проблема заключается в следующем:

Выведите "Yes", если существует матрица A размером m на n, где каждый элемент равен 0 или 1, так что

В противном случае выведите "Нет".

Для каждого теста предоставляются 2 массива:

r (сумма каждой строки в матрице)
с (сумма каждого столбца в матрице)

В уравнении:

m - длина массива r, где 1 <= m
n - длина массива c, где n <= 1000
ri является элементом r, где 0 <= ri <= n
cj является элементом c, где 0 <= cj <= m

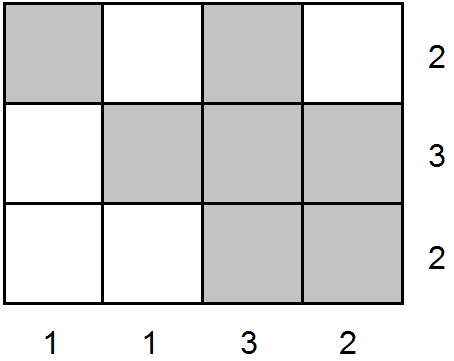
Пример "Да"

м = 3; n = 4; r = [2, 3, 2]; с = [1, 1, 3, 2];

Пример "Нет"

м = 3; n = 3; r = [0, 0, 3]; с = [0, 0, 3];

У меня есть решение, которое, по-видимому, дает правильные ответы, однако оно управляет только 12 / 38 тестами до того, как будет превышена 1 секунда процессорного времени.

Первоначально я написал код в ES5, а затем вернулся и преобразовался в ES3, чтобы попытаться повысить производительность. (изначально управлял 9 тестами как ES5). Кажется, не так уж много осталось, что я могу сделать с текущим алгоритмом, чтобы улучшить производительность (если я не ошибаюсь). Это приводит меня к мысли, что мой алгоритм виноват, и что для этого должен быть более быстрый алгоритм. Я сделал тонну чтения, пытаясь найти один и закончил с головной болью:)

Поэтому я обращаюсь к сообществу, чтобы узнать, может ли кто-нибудь предложить более быстрый алгоритм, чем я сейчас использую.

'use strict';

const ZEROS = (function (seed) {
  let string = seed;
  for (let i = 0; i < 19; i += 1) {
    string += seed;
  }

  return string;
}('00000000000000000000000000000000000000000000000000'));

const ZEROSLEN = ZEROS.length;

const permutate = function (n, ri) {
  const result = [];
  const memoize = {};
  let count = 0;
  do {
    const bin = count.toString(2);
    if (ZEROSLEN + bin.length > ZEROSLEN + n) {
      break;
    }

    if (!memoize[bin] && (bin.split('1').length - 1) === ri) {
      const string = (ZEROS + bin).slice(-n);
      const sLen = string.length;
      const perm = new Array(sLen);
      for (let i = sLen - 1; i >= 0; i -= 1) {
        perm[i] = +string[i];
      }

      memoize[bin] = result.push(perm);
    }

    count += 1;
  } while (count);

  return result;
};

const getMatrixSum = function (n, matrix) {
  const mLength = matrix.length;
  const rows = new Array(mLength);
  const a = new Array(n);
  const last = mLength - 1;
  for (let x = n - 1; x >= 0; x -= 1) {
    for (let y = last; y >= 0; y -= 1) {
      rows[y] = matrix[y][x];
    }

    let sum = 0;
    for (let i = rows.length - 1; i >= 0; i -= 1) {
      sum += rows[i];
    }

    a[x] = sum;
  }

  return a;
};

const isEqual = function (a, b) {
  const length = a.length;
  if (length !== b.length) {
    return false;
  }

  for (let i = length - 1; i >= 0; i -= 1) {
    if (a[i] !== b[i]) {
      return false;
    }
  }

  return true;
};

const addRow = function (i, prev, r, c, result) {
  if (result) {
    return result;
  }

  const n = c.length;
  const ri = r[i];
  if (ri < 0 || ri > n) {
    throw new RangeError('ri out of range');
  }

  const p = permutate(n, ri);
  const m = r.length;
  const rsLast = m - 1;
  const nextI = i + 1;
  for (let x = p.length - 1; x >= 0; x -= 1) {
    const permutation = p[x];
    const next = prev.slice();
    next.push(permutation);
    const sums = getMatrixSum(n, next);
    if (i < rsLast) {
      let memo = 0;
      for (let j = sums.length - 1; j >= 0; j -= 1) {
        if (sums[j] > c[j]) {
          memo += 1;
        }
      }

      if (!memo && addRow(nextI, next, r, c, result)) {
        return true;
      }
    } else if (isEqual(sums, c)) {
      return true;
    }
  }

  return false;
};

const isSolvable = function (r, c) {
  const m = r.length;
  const n = c.length;
  if (m < 1 || n > 1000) {
    throw new Error('Bad data');
  }

  for (let j = n; j >= 0; j -= 1) {
    const cj = c[j];
    if (cj < 0 || cj > m) {
      throw new RangeError('cj out of range');
    }
  }
  
  return addRow(0, [], r, c, false) ? 'Yes' : 'No';
};

console.log(isSolvable([2, 3, 2], [1, 1, 3, 2]));

console.log(isSolvable([0, 0, 3], [0, 0, 3]));

Возможно, стоит отметить, что тесты выполняются на версии SpiderMonkey JavaScript-C24.2.0

Refs:

https://en.wikipedia.org/wiki/Discrete_tomography

https://open.kattis.com/problems/tomography

3

javascript algorithm performance binary tomography-reconstruction

Источник

user592253 05 окт '17 в 14:12

2 ответа

Решение

Поскольку перестановки дают грубую силу, они должны быть последним средством при разработке алгоритмов, подобных этому. Большую часть времени они не нужны.

Как я уже говорил выше, у меня есть ощущение, что одной стратегией может быть сначала сортировка r а также c массивы по убыванию и начать с более крупных. У меня не было времени, чтобы реализовать код JS, чтобы разобраться с этим, поэтому у меня не было возможности тщательно протестировать. Пожалуйста, посмотрите, и если вы обнаружите недостаток, пожалуйста, укажите.

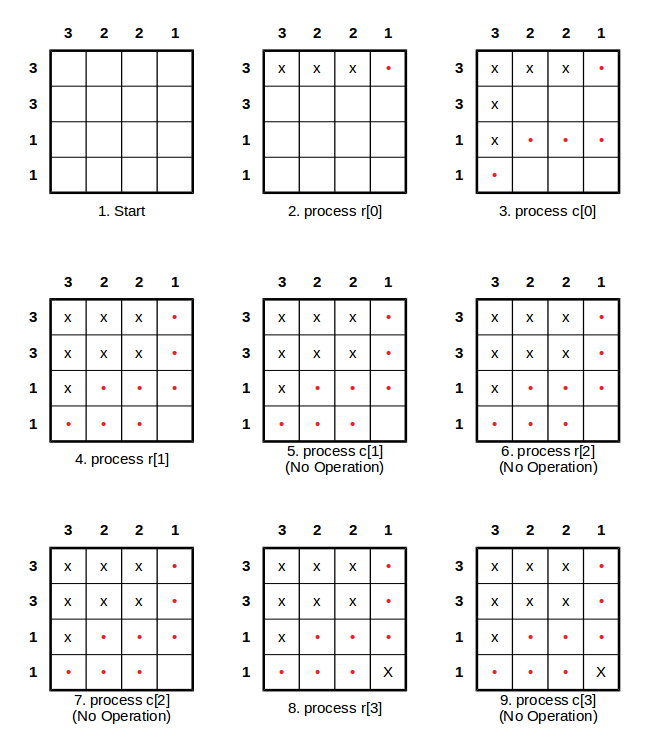
В приведенном ниже визуальном представлении алгоритма мы попробуем r = [1,3,1,3] а также c = [3,2,1,2], X обозначает занятую ячейку, а красная точка обозначает неприкасаемую ячейку, тогда как пустые, очевидно, являются свободными ячейками. Таким образом, в реальном алгоритме для представления ячейки нам нужен тип данных, такой как {value: false, avail: false} для красной точки в то время как {value: false, avail: true} будет означать свободное пространство. Или для экономии места и скорости вы можете использовать такой тип данных, как 0b00 для красной точки, 0b01 за свободное пространство и 0b1X для занятых (X здесь означает, что все равно) клетки.

Примечание: стоит упомянуть Шаг 3, где мы обрабатываем c[0], После того, как мы вставим три X s мы должны проверить строки, занятые X s, чтобы обновить состояние пустых ячеек в этих строках. В этом случае для r[2] все пустые клетки становятся неприкасаемыми.

Редактировать:

Ну, ладно... Так как нам не нужно строить решение в виде двумерного массива, подобного структуре, а нужен только ответ на вопрос, являются ли предоставленные данные значимыми или нет, я пришел к другой и более простой идее, которая по существу основана на вышеуказанный подход. Я действительно не думаю, что это может быть быстрее, чем это. Он решает доску 999 на 1000 за 50 мс.

Позволяет войти в это.

Вход r = [2, 3, 2]; c = [1, 1, 3, 2]; Однако одно важное условие здесь c а также r массивы должны суммироваться до одного числа. Мы можем просто проверить это в начале нашего кода или оставить его, выполнить следующие шаги, и если они проходят проверку, только если c полон 0с. Следующий код предпочитает последний подход.
Сортировать r по убыванию так; r = [3, 2, 2]; c = [1, 1, 3, 2];
Попробуйте уменьшить r[0] (3 в первом случае) много ненулевых элементов c на 1. Теперь c становится [0, 0, 2, 2], Если не получится, не пытайтесь больше и вернитесь false,
Теперь, когда мы закончили с строкой r[0], рекурсивно вызывать функцию с r = [2, 2]; c = [0, 0, 2, 2]; в то время как r.length больше 0 и аргумент bool b является true, Следующий звонок будет r = [2]; c = [0, 0, 1, 1]; и наконец r = []; c = [0, 0, 0, 0];
Если, наконец, рекурсивный вызов с пустым r вызывается, затем проверьте b является true и все предметы c являются 0, (b && cs.every(n => !n)).

Я верю, что это просто отлично, но так как у меня нет ваших тестов, вам стоит попробовать. Я уверен, что он пройдет проверку временем. Вот код в самом простом. Здесь я тестирую rs = [7,3,5,4,6,2,8] а также cs = [7,1,6,3,4,5,2,7], Это выглядит как;

  71634527
7 x xxxxxx
3 x x    x
5 x x xx x
4 x x  x x
6 x xxxx x
2 x      x
8 xxxxxxxx

function nonogram(rs,cs){
  function runner(rs,cs, b = true){//console.log(rs,cs,b)
    return b && rs.length ? runner(rs.slice(1),                                 // rows argument
                                   cs.map(e => rs[0] ? e ? (b = !--rs[0], e-1)  // cols argument
                                                         : e
                                                     : e),
                                   b)                                           // bool argument
                          : b && cs.every(n => !n);
  }
return runner(rs.sort((a,b) => b-a), cs);
}

var rs = [7,3,5,4,6,2,8],
    cs = [7,1,6,3,4,5,2,7],
    result;
console.time("test");
result = nonogram(rs,cs);
console.timeEnd("test");
console.log(result);

2

Источник

user4543207 06 окт '17 в 12:55

Другие вопросы по тегам javascript algorithm performance binary tomography-reconstruction

user592253 06 окт '17 в 10:50 2017-10-06 10:50 · Accepted Answer · 2017-10-06 10:50

У меня не было готовых к тесту, но я нашел гораздо более эффективный алгоритм после события.

'use strict';

const sortNumber = function (a, b) {
  return b - a;
};

const isSolvable = function (r, c) {
  const m = r.length;
  const n = c.length;
  if (m < 1 || n > 1000) {
    throw new Error('Bad data');
  }

  for (let j = n; j >= 0; j -= 1) {
    const cj = c[j];
    if (cj < 0 || cj > m) {
      throw new RangeError('cj out of range');
    }
  }

  while (r.length) {
    c.sort(sortNumber);
    const ri = r.pop();
    if (ri < 0 || ri > n) {
      throw new RangeError('ri out of range');
    }

    if (ri) {
      if (!c[ri - 1]) {
        return 'No';
      }

      for (let j = ri - 1; j >= 0; j -= 1) {
        c[j] -= 1;
      }
    }
  }

  for (let j = n - 1; j >= 0; j -= 1) {
    if (c[j]) {
      return 'No';
    }
  }

  return 'Yes';
};

console.log(isSolvable([2, 3, 2], [1, 1, 3, 2]));

console.log(isSolvable([0, 0, 3], [0, 0, 3]));