Не удается получить RK4 для определения положения тела на орбите в Python

Question

Я пытаюсь определить положение тела, вращающегося вокруг гораздо более массивного тела, используя идеализацию, согласно которой гораздо более массивное тело не двигается. Я пытаюсь найти положение в декартовых координатах, используя Runge-Kutta 4-го порядка в python.

Вот мой код:

dt = .1
t = np.arange(0,10,dt)

vx = np.zeros(len(t))
vy = np.zeros(len(t))
x = np.zeros(len(t))
y = np.zeros(len(t))

vx[0] = 10 #initial x velocity
vy[0] = 10 #initial y velocity
x[0] = 10 #initial x position
y[0] = 0 #initial y position

M = 20

def fx(x,y,t): #x acceleration
     return -G*M*x/((x**2+y**2)**(3/2))

def fy(x,y,t): #y acceleration
     return -G*M*y/((x**2+y**2)**(3/2))

def rkx(x,y,t,dt): #runge-kutta for x

     kx1 = dt * fx(x,y,t)
     mx1 = dt * x
     kx2 = dt * fx(x + .5*kx1, y + .5*kx1, t + .5*dt)
     mx2 = dt * (x + kx1/2)
     kx3 = dt * fx(x + .5*kx2, y + .5*kx2, t + .5*dt)
     mx3 = dt * (x + kx2/2)
     kx4 = dt * fx(x + kx3, y + x3, t + dt)
     mx4 = dt * (x + kx3)

     return (kx1 + 2*kx2 + 2*kx3 + kx4)/6
     return (mx1 + 2*mx2 + 2*mx3 + mx4)/6

 def rky(x,y,t,dt): #runge-kutta for y

     ky1 = dt * fy(x,y,t)
     my1 = dt * y
     ky2 = dt * fy(x + .5*ky1, y + .5*ky1, t + .5*dt)
     my2 = dt * (y + ky1/2)
     ky3 = dt * fy(x + .5*ky2, y + .5*ky2, t + .5*dt)
     my3 = dt * (y + ky2/2)
     ky4 = dt * fy(x + ky3, y + ky3, t + dt)
     my4 = dt * (y + ky3)

     return (ky1 + 2*ky2 + 2*ky3 + ky4)/6
     return (my1 + 2*my2 + 2*my3 + my4)/6

for n in range(1,len(t)): #solve using RK4 functions
    vx[n] = vx[n-1] + fx(x[n-1],y[n-1],t[n-1])*dt
    vy[n] = vy[n-1] + fy(x[n-1],y[n-1],t[n-1])*dt
    x[n] = x[n-1] + vx[n-1]*dt
    y[n] = y[n-1] + vy[n-1]*dt

Первоначально, независимо от того, каким образом я настраивал код, я получал ошибку в цикле for, либо "объект типа" float "не имеет len()" (я не понимал, на что может ссылаться float python), или "установка элемента массива с помощью последовательности" (я также не понял, что это за последовательность). Мне удалось избавиться от ошибок, но мои результаты просто неверны. Я получаю массивы vx и vy по 10 с, массив целых чисел x от 10 до 109 и массив целых чисел от 0 до 99.

Я подозреваю, что есть проблемы с fx(x,y,t) и fy(x,y,t) или со способом, которым я кодировал функции runge-kutta, чтобы пойти с fx и fy, потому что я использовал ту же самую runge -кутта кода для других функций и он отлично работает.

Я очень ценю любую помощь в выяснении, почему мой код не работает. Спасибо.

Answer 1

физика

Закон Ньютона дает вам ОДУ второго порядка u''=F(u) с u=[x,y], С помощью v=[x',y'] вы получаете систему первого заказа

u' = v
v' = F(u)

который является 4-мерным и должен быть решен с использованием 4-мерного состояния. Единственное доступное сокращение - это использование законов Кеплера, которые позволяют привести систему к скалярному порядку на один ОДУ для угла. Но это не задача здесь.

Метод Эйлера

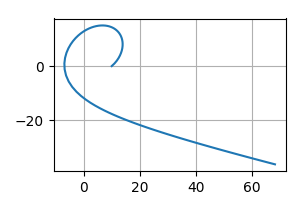
Вы правильно реализовали метод Эйлера для вычисления значений в последнем цикле вашего кода. То, что он может выглядеть нефизическим, может быть связано с тем, что метод Эйлера непрерывно увеличивает орбиту, поскольку он движется за пределы выпуклых траекторий, следующих за касательной. В вашей реализации эта внешняя спираль может быть видна для G=100,

Это может быть уменьшено путем выбора меньшего размера шага, такого как dt=0.001,

Вы должны выбрать время интеграции, чтобы быть хорошей частью полной орбиты, чтобы получить презентабельный результат, с указанными выше параметрами вы получите около 2 циклов, что хорошо.

Реализация РК4

Вы сделали несколько ошибок. Каким-то образом вы потеряли скорости, обновления положения должны быть основаны на скоростях.

Тогда вы должны были остановиться на fx(x + .5*kx1, y + .5*kx1, t + .5*dt) пересмотреть ваш подход, так как он несовместим с любым соглашением об именах. Последовательный, правильный вариант

fx(x + .5*kx1, y + .5*ky1, t + .5*dt) 

который показывает, что вы не можете отделить интеграцию связанной системы, так как вам нужно y обновления вместе с x Обновления. Кроме того, значения функции являются ускорениями, поэтому обновляются скорости. Обновления положения используют скорости текущего состояния. Таким образом, шаг должен начинаться как

 kx1 = dt * fx(x,y,t) # vx update
 mx1 = dt * vx        # x update
 ky1 = dt * fy(x,y,t) # vy update
 my1 = dt * vy        # y update

 kx2 = dt * fx(x + 0.5*mx1, y + 0.5*my1, t + 0.5*dt)
 mx2 = dt * (vx + 0.5*kx1/2)
 ky2 = dt * fy(x + 0.5*mx1, y + 0.5*my1, t + 0.5*dt)
 my2 = dt * (vy + 0.5*ky1/2)

и т.п.

Однако, как вы видите, это уже начинает становиться громоздким. Соберите состояние в вектор и используйте векторную функцию для системных уравнений

M, G = 20, 100
def orbitsys(u):
     x,y,vx,vy = u
     r = np.hypot(x,y)
     f = G*M/r**3
     return np.array([vx, vy, -f*x, -f*y]);

Затем вы можете использовать реализацию кулинарной книги шага Эйлера или Рунге-Кутты.

def Eulerstep(f,u,dt): return u+dt*f(u)

def RK4step(f,u,dt):
    k1 = dt*f(u)
    k2 = dt*f(u+0.5*k1)
    k3 = dt*f(u+0.5*k2)
    k4 = dt*f(u+k3)
    return u + (k1+2*k2+2*k3+k4)/6

и объединить их в интеграционный цикл

def Eulerintegrate(f, y0, tspan):
    y = np.zeros([len(tspan),len(y0)])
    y[0,:]=y0
    for k in range(1, len(tspan)):
        y[k,:] = Eulerstep(f, y[k-1], tspan[k]-tspan[k-1])
    return y


def RK4integrate(f, y0, tspan):
    y = np.zeros([len(tspan),len(y0)])
    y[0,:]=y0
    for k in range(1, len(tspan)):
        y[k,:] = RK4step(f, y[k-1], tspan[k]-tspan[k-1])
    return y

и вызвать их с вашей данной проблемой

dt = .1
t = np.arange(0,10,dt)
y0 = np.array([10, 0.0, 10, 10])

sol_euler = Eulerintegrate(orbitsys, y0, t)
x,y,vx,vy = sol_euler.T
plt.plot(x,y)

sol_RK4 = RK4integrate(orbitsys, y0, t)
x,y,vx,vy = sol_RK4.T
plt.plot(x,y)

Answer 2

Вы не используете rkx, rky функционирует где угодно! Есть два return в конце определения функции вы должны использовать return [(kx1 + 2*kx2 + 2*kx3 + kx4)/6, (mx1 + 2*mx2 + 2*mx3 + mx4)/6] (как указано @eapetcho). Кроме того, ваша реализация Runge-Kutta мне не ясна.

У тебя есть dv/dt так что вы решаете за v а затем обновить r соответственно.

for n in range(1,len(t)): #solve using RK4 functions
    vx[n] = vx[n-1] + rkx(vx[n-1],vy[n-1],t[n-1])*dt
    vy[n] = vy[n-1] + rky(vx[n-1],vy[n-1],t[n-1])*dt
    x[n] = x[n-1] + vx[n-1]*dt
    y[n] = y[n-1] + vy[n-1]*dt

Вот моя версия кода

import numpy as np

#constants
G=1
M=1
h=0.1

#initiating variables
rt = np.arange(0,10,h)
vx = np.zeros(len(rt))
vy = np.zeros(len(rt))
rx = np.zeros(len(rt))
ry = np.zeros(len(rt))

#initial conditions
vx[0] = 10 #initial x velocity
vy[0] = 10 #initial y velocity
rx[0] = 10 #initial x position
ry[0] = 0 #initial y position

def fx(x,y): #x acceleration
     return -G*M*x/((x**2+y**2)**(3/2))

def fy(x,y): #y acceleration
     return -G*M*y/((x**2+y**2)**(3/2))

def rk4(xj, yj):
    k0 = h*fx(xj, yj)
    l0 = h*fx(xj, yj)

    k1 = h*fx(xj + 0.5*k0 , yj + 0.5*l0)
    l1 = h*fy(xj + 0.5*k0 , yj + 0.5*l0)

    k2 = h*fx(xj + 0.5*k1 , yj + 0.5*l1)
    l2 = h*fy(xj + 0.5*k1 , yj + 0.5*l1)

    k3 = h*fx(xj + k2, yj + l2)
    l3 = h*fy(xj + k2, yj + l2)

    xj1 = xj + (1/6)*(k0 + 2*k1 + 2*k2 + k3)
    yj1 = yj + (1/6)*(l0 + 2*l1 + 2*l2 + l3)
    return (xj1, yj1)

for t in range(1,len(rt)):
    nv = rk4(vx[t-1],vy[t-1])
    [vx[t],vy[t]] = nv
    rx[t] = rx[t-1] + vx[t-1]*h
    ry[t] = ry[t-1] + vy[t-1]*h

Я подозреваю, что есть проблемы с fx(x,y,t) и fy(x,y,t)

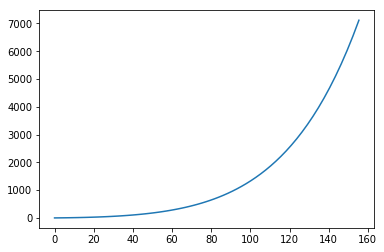
Это тот случай, я только что проверил свой код для fx=3 а также fy=y и я получил хорошую траекторию.

Здесь ry против rx сюжет: