Спектр, рассчитанный с использованием Matlab FFT, не дает согласованного результата для разных длин выборки (одинаковое количество точек, но разные F)?

Question

Я хотел бы построить профиль морщинистости (из измерений AFM), но все еще есть то, что я неправильно понимаю в отношении БПФ (особенно в документации Matlab).

Я хочу сравнить два измерения, ака два профиля морщинистости. Они были сделаны на одной поверхности, они расходятся только на том факте, что один сделан на более короткой длине, чем другой. Тем не менее, для каждого профиля у меня одинаковое количество выборок (N=512 здесь). Допустим, это мои профили, t10 а также t100 будучи абсциссой, по которой производится мера, и d10 а также d100 вертикальная координата, ak высота измерения в профиле морщинистости.

N=512;
t10 = linspace(0,10, N);
t100= linspace(0,100, N);
d10  = sin(2*pi*0.23 .*t10)+cos(2*pi*12 .*t10);
d100 = sin(2*pi*0.23 .*t100)+cos(2*pi*12 .*t100);

Поскольку измеряется одна и та же поверхность, но с разным пространственным разрешением, то есть с разным периодом выборки, односторонний спектр амплитуд этих профилей морщинистости должен перекрываться, не так ли?

В отличие от того, что я должен получить, у меня есть следующие графики: 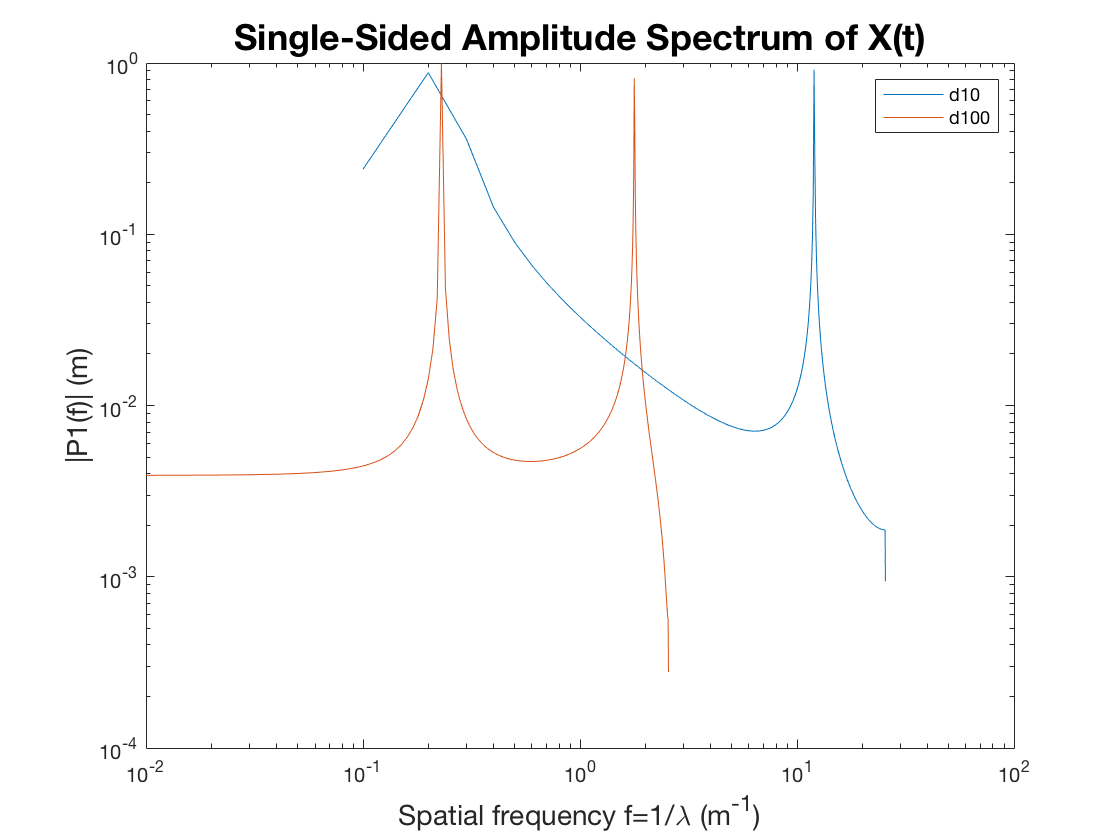а также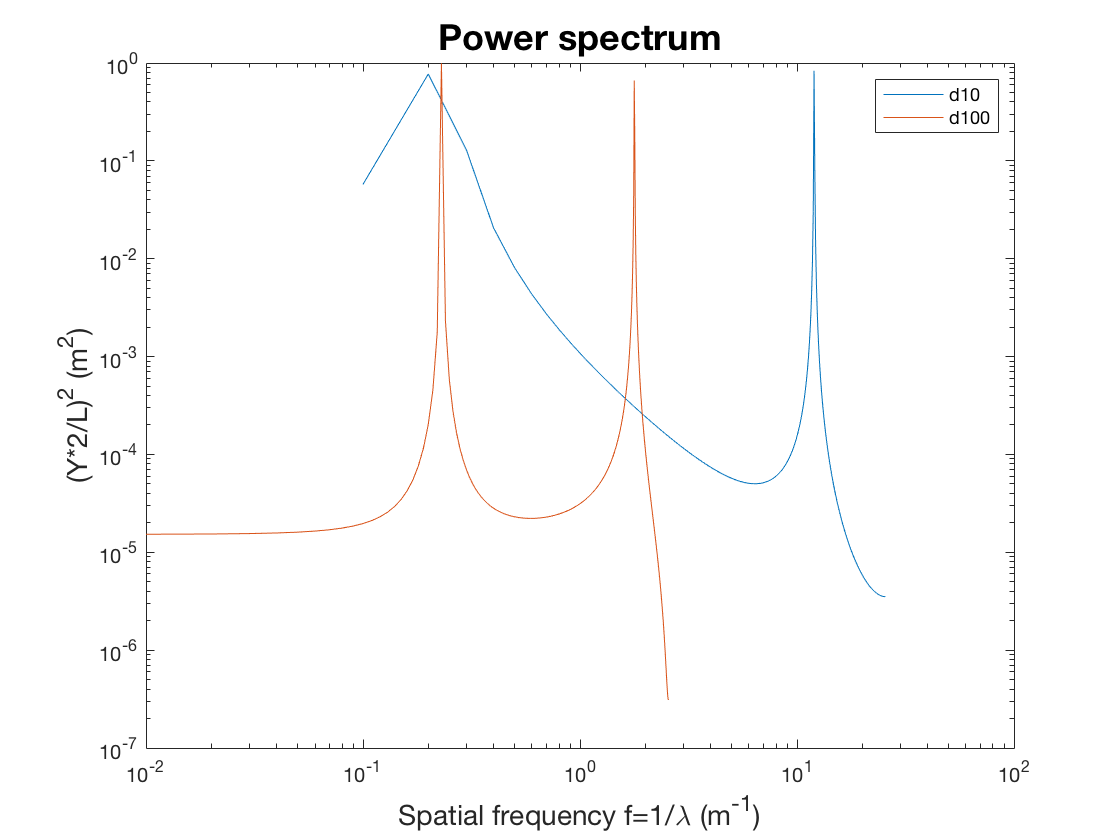

Используя следующую функцию:

function [f,P1,S1] = FFT_PowerSpectrumDensity(time,signal,flagfig)
H=signal;
X=time;
ell=length(X);
L = ell;% 2^(nextpow2(ell)-1) % Next power of 2 from length of the signal
deltaTime = mean(diff(X));
Fs=1/deltaTime; %% mean sampling frequency

%% Compute the Fourier transform of the signal.
Y = fft(H);
%% Compute the two-sided spectrum P2. Then compute the single-sided spectrum P1 based on P2 and the even-valued signal length L.
P2 = abs(Y/L); % abs(fft(signal Y)) / Length_of_signal
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = Fs*(0:(L/2))/L;
if flagfig~=0
    figure(flagfig)
    loglog(f,P1)
    title('Single-Sided Amplitude Spectrum of X(t)','FontSize',18)
    xlabel('Spatial frequency f=1/\lambda (m^{-1})','FontSize',14)
    ylabel('|P1(f)| (m)','FontSize',14)
end

S = (Y.*conj(Y)).*(2/L).^2; % power spectral density

S1 = S(1:L/2+1);
S1(2:end-1) = S1(2:end-1);
%% Power spectrum (amplitude = a^2+b^2), in length^2
if flagfig~=0
    figure(flagfig+1)
    loglog(f,S1)
    title('Power spectrum','FontSize',18)
    xlabel('Spatial frequency f=1/\lambda (m^{-1})','FontSize',14)
    ylabel('(Y*2/L)^2 (m^2)','FontSize',14)
end
end

Я вызываю эту функцию, например, используя следующую команду:

[f10, S10]= FFT_PowerSpectrumDensity(t10, d10, 10);

Должен ли я использовать L=2^pow2(ell)-1)? Я понял, что это обеспечивает лучший вход для функции FFT? Кроме того, я совершенно не уверен в отношении большинства единиц и значений, которые я должен найти.

Спасибо за вашу помощь, исправления и предложения.

Answer 1

Ваша проблема в вашем входном сигнале:

N=512;
t100 = linspace(0,100, N);
d100 = sin(2*pi*0.23 .*t100)+cos(2*pi*12 .*t100);

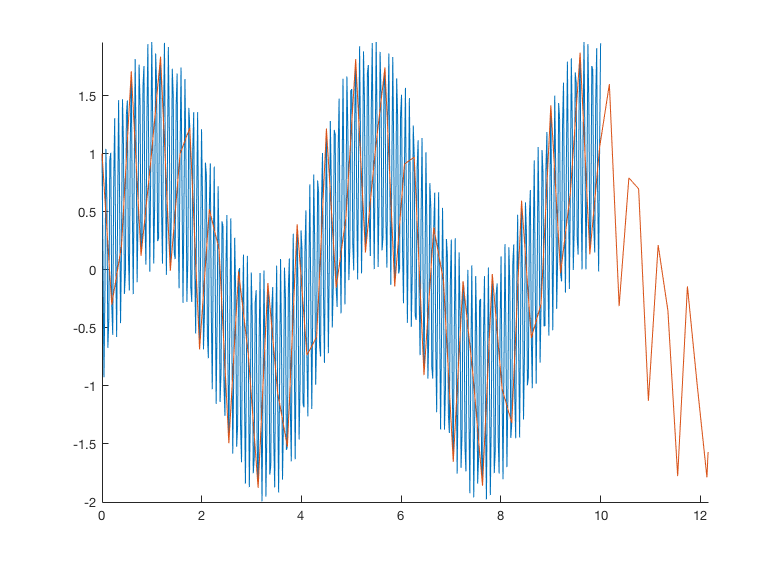
d100 недостаточно отобран. У тебя есть cos(0) в образце кулака, то cos(2*pi*12*0.1953 знак равно cos(2*pi*2.3436) в вашем втором образце. Это 2.3 периода спустя!

Заговор d100 а также d10 и увеличение масштаба первых 10 с сигнала выявляет проблему:

Следовательно, низкочастотный компонент оценивается правильно (широкий пик для d10 из-за нескольких периодов, а не целое число из них), но более высокочастотный компонент, псевдоним для d100появляется на более низкой частоте.

Кстати, что касается изменения длины преобразования до степени двойки: это ускорит вычисления в целом, но в этом случае у вас уже есть сигнал степени двух длин. Результаты не будут лучше, это просто скорость вычислений.