Плотная линия с PyPlot

Question

У меня есть следующий простой скрипт, который строит график:

import matplotlib.pyplot as plt
import numpy as np

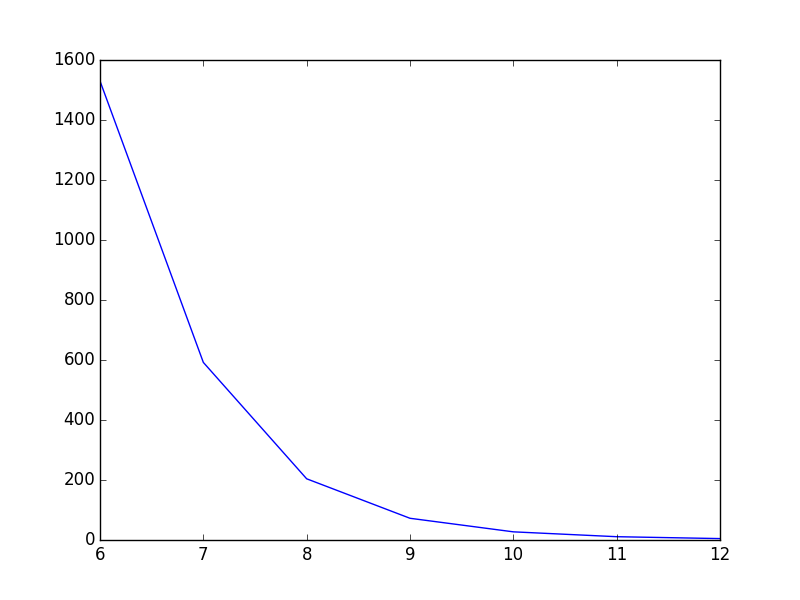
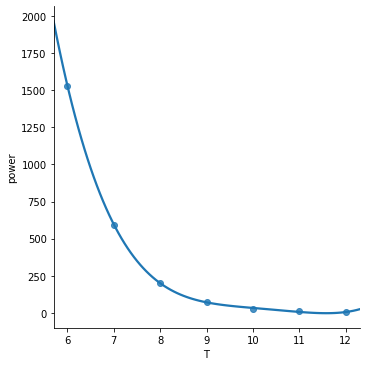
T = np.array([6, 7, 8, 9, 10, 11, 12])
power = np.array([1.53E+03, 5.92E+02, 2.04E+02, 7.24E+01, 2.72E+01, 1.10E+01, 4.70E+00])

plt.plot(T,power)
plt.show()

Как и сейчас, линия идет прямо из точки в точку, что выглядит хорошо, но, на мой взгляд, может быть лучше. Я хочу сгладить грань между точками. В Gnuplot я бы заговорил с smooth cplines,

Есть ли простой способ сделать это в PyPlot? Я нашел несколько уроков, но все они кажутся довольно сложными.

Answer 1

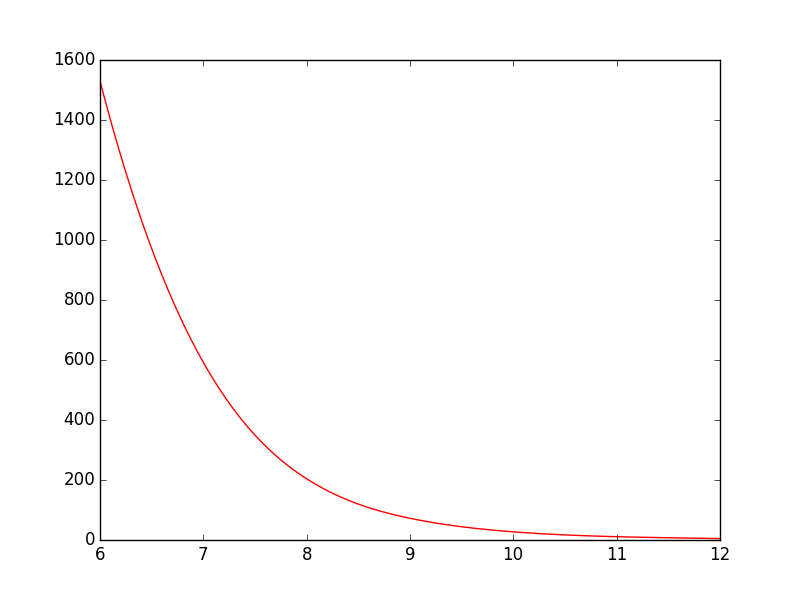
Вы могли бы использовать scipy.interpolate.spline чтобы сгладить ваши данные самостоятельно:

from scipy.interpolate import spline

xnew = np.linspace(T.min(),T.max(),300) #300 represents number of points to make between T.min and T.max

power_smooth = spline(T,power,xnew)

plt.plot(xnew,power_smooth)
plt.show()

---

Сплайн устарел в scipy 0.19.0, используйте класс Bspline.

Переключение с spline в Bspline не простая копия / вставка и требует небольшой настройки:

from scipy.interpolate import make_interp_spline, BSpline

xnew = np.linspace(T.min(),T.max(),300) #300 represents number of points to make between T.min and T.max

spl = make_interp_spline(T, power, k=3) #BSpline object
power_smooth = spl(xnew)

plt.plot(xnew,power_smooth)
plt.show()

---

До:

После:

Answer 2

В этом примере сплайн работает хорошо, но если функция не является гладкой по своей природе и вы хотите иметь сглаженную версию, вы также можете попробовать:

from scipy.ndimage.filters import gaussian_filter1d

ysmoothed = gaussian_filter1d(y, sigma=2)
plt.plot(x, ysmoothed)
plt.show()

если вы увеличите сигму, вы можете получить более сглаженную функцию.

Answer 3

Увидеть scipy.interpolate документация для некоторых примеров.

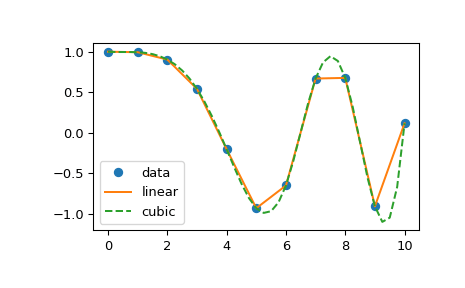
Следующий пример демонстрирует его использование для интерполяции линейным и кубическим сплайном:

>>> from scipy.interpolate import interp1d

>>> x = np.linspace(0, 10, num=11, endpoint=True)
>>> y = np.cos(-x**2/9.0)
>>> f = interp1d(x, y)
>>> f2 = interp1d(x, y, kind='cubic')

>>> xnew = np.linspace(0, 10, num=41, endpoint=True)
>>> import matplotlib.pyplot as plt
>>> plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')
>>> plt.legend(['data', 'linear', 'cubic'], loc='best')
>>> plt.show()

Answer 4

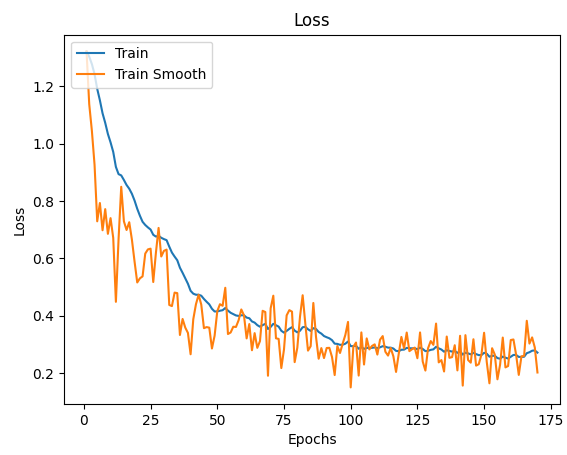
Одна из самых простых реализаций, которую я нашел, - это использовать экспоненциальную скользящую среднюю, которую использует Tensorboard:

      def smooth(scalars: List[float], weight: float) -> List[float]:  # Weight between 0 and 1
    last = scalars[0]  # First value in the plot (first timestep)
    smoothed = list()
    for point in scalars:
        smoothed_val = last * weight + (1 - weight) * point  # Calculate smoothed value
        smoothed.append(smoothed_val)                        # Save it
        last = smoothed_val                                  # Anchor the last smoothed value
        
    return smoothed


ax.plot(x_labels, smooth(train_data, .9), x_labels, train_data)

Answer 5

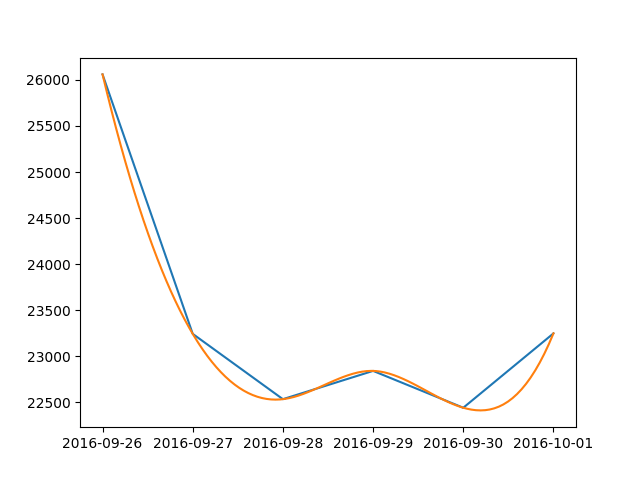
Вот простое решение для дат:

       from scipy.interpolate import make_interp_spline
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.dates as dates
from datetime import datetime

data = {
    datetime(2016, 9, 26, 0, 0): 26060, datetime(2016, 9, 27, 0, 0): 23243,
    datetime(2016, 9, 28, 0, 0): 22534, datetime(2016, 9, 29, 0, 0): 22841,
    datetime(2016, 9, 30, 0, 0): 22441, datetime(2016, 10, 1, 0, 0): 23248 
}
#create data
date_np = np.array(list(data.keys()))
value_np = np.array(list(data.values()))
date_num = dates.date2num(date_np)
# smooth
date_num_smooth = np.linspace(date_num.min(), date_num.max(), 100) 
spl = make_interp_spline(date_num, value_np, k=3)
value_np_smooth = spl(date_num_smooth)
# print
plt.plot(date_np, value_np)
plt.plot(dates.num2date(date_num_smooth), value_np_smooth)
plt.show()

Answer 6

Я предполагаю, что вы имеете в виду подгонку кривой, а не сглаживание в контексте вашего вопроса. PyPlot не имеет встроенной поддержки для этого, но вы можете легко реализовать некоторое базовое подгонку кривой, например код, показанный здесь, или если вы используете GuiQwt, он имеет модуль подбора кривой. (Вы также можете украсть код из SciPy, чтобы сделать это).

Answer 7

Стоит время на чтобы посмотреть на потратитьseabornто, для построения сглаженных линий.

Функция seaborn lmplot построит график данных и соответствия регрессионной модели.

Следующее иллюстрирует как полиномиальную, так и низкую аппроксимацию :

      import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

T = np.array([6, 7, 8, 9, 10, 11, 12])
power = np.array([1.53E+03, 5.92E+02, 2.04E+02, 7.24E+01, 2.72E+01, 1.10E+01, 4.70E+00])

df = pd.DataFrame(data = {'T': T, 'power': power})
    
sns.lmplot(x='T', y='power', data=df, ci=None, order=4, truncate=False)
sns.lmplot(x='T', y='power', data=df, ci=None, lowess=True, truncate=False)

В order = 4полиномиальная подгонка превышает этот набор данных игрушек. Я не показываю это здесь, но order = 2 а также order = 3 дал худшие результаты.

В lowess = True fit не соответствует этому крошечному набору данных, но может дать лучшие результаты на больших наборах данных.

Проверьте Сиборн регрессионного учебник для большего количества примеров.

Answer 8

Другой вариант, который немного изменяет функцию в зависимости от используемых вами параметров:

      from statsmodels.nonparametric.smoothers_lowess import lowess

def smoothing(x, y):
    lowess_frac = 0.15  # size of data (%) for estimation =~ smoothing window
    lowess_it = 0
    x_smooth = x
    y_smooth = lowess(y, x, is_sorted=False, frac=lowess_frac, it=lowess_it, return_sorted=False)
    return x_smooth, y_smooth

Это было лучше, чем другие ответы для моего конкретного случая применения.