Инвариантный по времени предиктор наклона и перехвата в модели кривой скрытого роста в OpenMx
Я пытаюсь выяснить, как правильно добавить предиктор наклона и перехват в модели кривой скрытого роста в пакете OpenMx для R.
Я хотел бы предсказать наклон и перехват, скажем, от пола в очень простой модели кривой роста. Ради этого вопроса, скажем, это модель, описанная в документации здесь.
Что бы я добавил, чтобы включить не зависящий от времени предиктор наклона и перехвата? В MPlus я бы написал i on male; и я бы получил оценку пути от переменной пола до скрытого перехвата. Чтобы сделать то же самое в OpenMx, я бы просто добавил эту спецификацию пути? Нужно ли мне переопределить какие-либо значения по умолчанию, чтобы я не оценивал дисперсию или средний путь для этой переменной манифеста (или так я делаю)?
Для удобства ниже приведен код простой кривой роста и то, что я добавил для предиктора. Однако, когда я добавляю предиктор, я получаю ошибку "ковариационная матрица не является положительно определенной". Это то, что я вижу в реальных данных.
Примечание: этот вопрос кросс-опубликован на форуме OpenMx.
myLongitudinalData=data.frame(x1=rnorm(100),
x2=rnorm(100),
x3=rnorm(100),
x4=rnorm(100),
x5=rnorm(100),
male=round(runif(100,0,1)))
require(OpenMx)
growthCurveModel <- mxModel("Linear Growth Curve Model Path Specification",
type="RAM",
mxData(
myLongitudinalData,
type="raw"
),
manifestVars=c("x1","x2","x3","x4","x5"),
latentVars=c("intercept","slope"),
# residual variances
mxPath(
from=c("x1","x2","x3","x4","x5"),
arrows=2,
free=TRUE,
values = c(1, 1, 1, 1, 1),
labels=c("residual","residual","residual","residual","residual")
),
# latent variances and covariance
mxPath(
from=c("intercept","slope"),
arrows=2,
connect="unique.pairs",
free=TRUE,
values=c(1, 1, 1),
labels=c("vari", "cov", "vars")
),
# intercept loadings
mxPath(
from="intercept",
to=c("x1","x2","x3","x4","x5"),
arrows=1,
free=FALSE,
values=c(1, 1, 1, 1, 1)
),
# slope loadings
mxPath(
from="slope",
to=c("x1","x2","x3","x4","x5"),
arrows=1,
free=FALSE,
values=c(0, 1, 2, 3, 4)
),
# manifest means
mxPath(
from="one",
to=c("x1", "x2", "x3", "x4", "x5"),
arrows=1,
free=FALSE,
values=c(0, 0, 0, 0, 0)
),
# latent means
mxPath(
from="one",
to=c("intercept", "slope"),
arrows=1,
free=TRUE,
values=c(1, 1),
labels=c("meani", "means")
)
) # close model
growthCurveFit <- mxRun(growthCurveModel)
summary(growthCurveFit)
Моя попытка добавить предиктор - я добавляю переменную пола в переменные манифеста, а затем создаю определение пути от нее к скрытым переменным (внизу):
growthCurveModel2 <- mxModel("Linear Growth Curve Model Path Specification",
type="RAM",
mxData(
myLongitudinalData,
type="raw"
),
manifestVars=c("x1","x2","x3","x4","x5","male"),
latentVars=c("intercept","slope"),
# residual variances
mxPath(
from=c("x1","x2","x3","x4","x5"),
arrows=2,
free=TRUE,
values = c(1, 1, 1, 1, 1),
labels=c("residual","residual","residual","residual","residual")
),
# latent variances and covariance
mxPath(
from=c("intercept","slope"),
arrows=2,
connect="unique.pairs",
free=TRUE,
values=c(1, 1, 1),
labels=c("vari", "cov", "vars")
),
# intercept loadings
mxPath(
from="intercept",
to=c("x1","x2","x3","x4","x5"),
arrows=1,
free=FALSE,
values=c(1, 1, 1, 1, 1)
),
# slope loadings
mxPath(
from="slope",
to=c("x1","x2","x3","x4","x5"),
arrows=1,
free=FALSE,
values=c(0, 1, 2, 3, 4)
),
# manifest means
mxPath(
from="one",
to=c("x1", "x2", "x3", "x4", "x5"),
arrows=1,
free=FALSE,
values=c(0, 0, 0, 0, 0)
),
# latent means
mxPath(
from="one",
to=c("intercept", "slope"),
arrows=1,
free=TRUE,
values=c(1, 1),
labels=c("meani", "means")
),
mxPath(
from="male",
to=c("intercept", "slope"),
arrows=1,
free=TRUE,
values=c(1,1),
labels=c("iOnMale", "sOnMale"))
) # close model
growthCurveFit2 <- mxRun(growthCurveModel2)
summary(growthCurveFit2)
1 ответ
Я полагаю, что я понял это - необходимо указать дисперсию предиктора и пути средней структуры, в соответствии с этой диаграммой из книги Sline Kline (2011):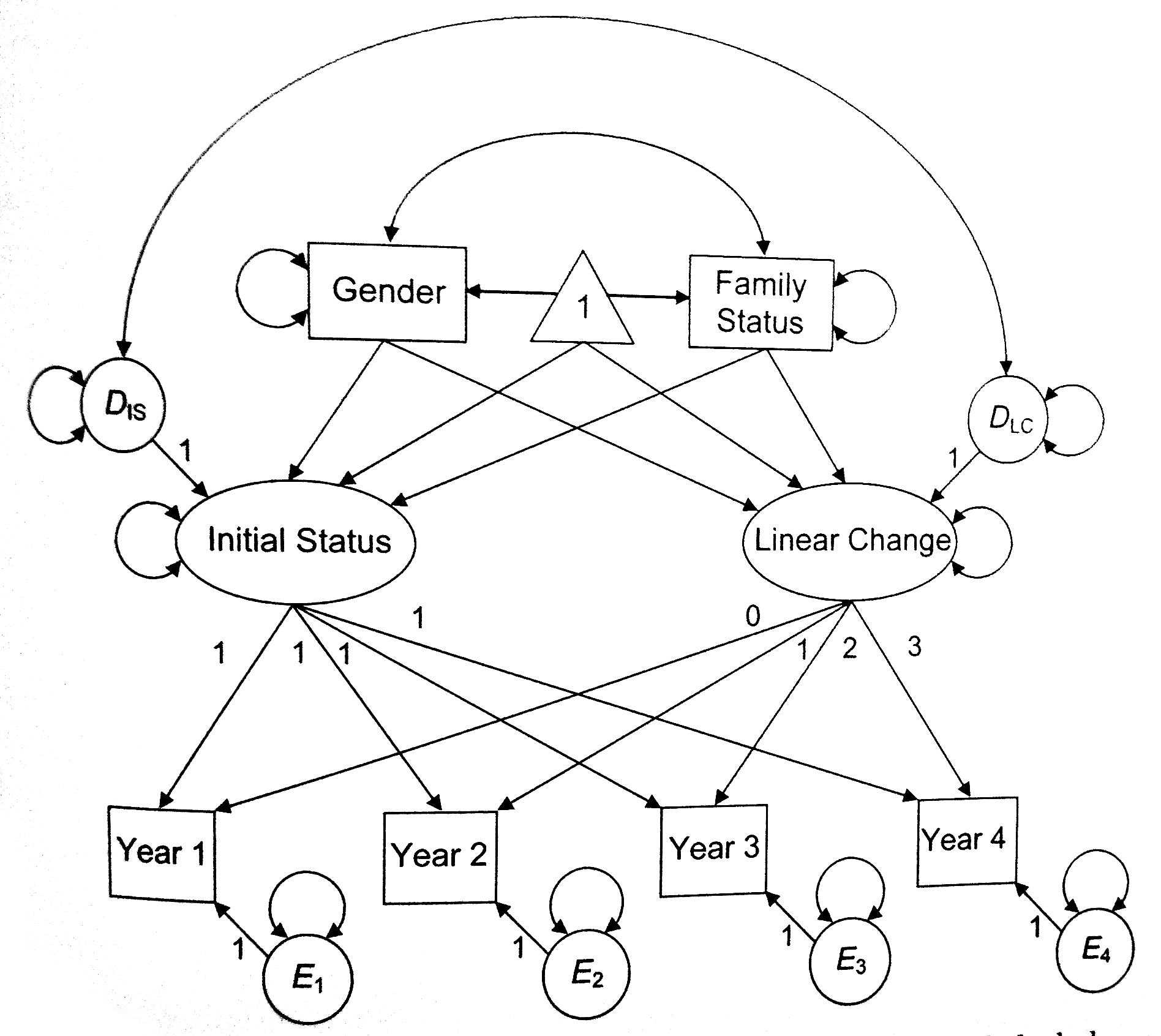
В MPlus я думаю, что по умолчанию для регрессии скрытого наклона и перехвата на предикторе является установка среднего пути к структуре на 0 и пути отклонения на 1. Я не уверен на 100% в этом, но это дало мне идентичный параметризация и очень похожие оценки. Итак, я добавил этот фрагмент ко второй модели выше:
#Predictor mean structure
mxPath(
from="one",
to="male",
arrows=1,
free=FALSE,
values = 0
),
#Predictor Variance
mxPath(
from="male",
arrows=2,
free=FALSE,
values = 1
)
Клайн, РБ (2011). Принципы и практика моделирования структурных уравнений. Гилфорд пресс.