Как я могу улучшить качество изображения Гильберта?

Question

Этот метод сканирования изображения основан на кривой Гильберта. Кривая выглядит так (от 1 до 6 порядка):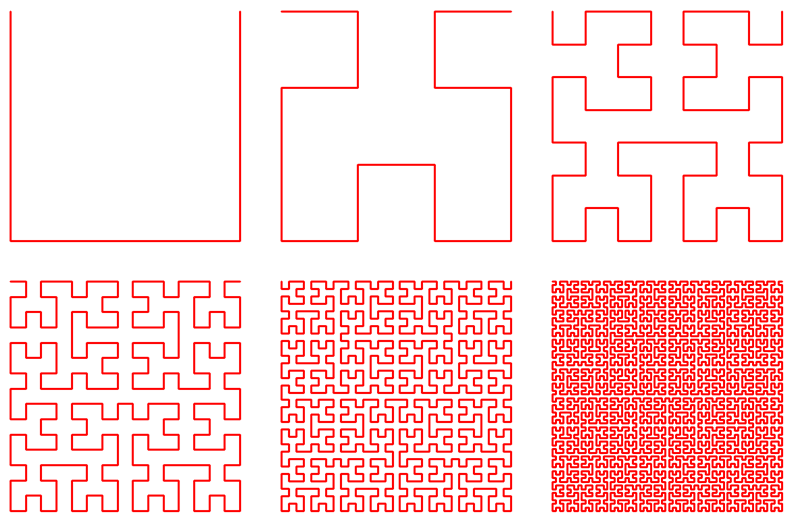

Может использоваться для сканирования изображения. Так, например, мой код для кривой 3-го порядка:

Hilbert=[C(1,1) C(1,2) C(2,2) C(2,1) C(3,1) C(4,1) C(4,2) C(3,2) C(3,3) C(4,3) C(4,4) C(3,4)...
      C(2,4) C(2,3) C(1,3) C(1,4) C(1,5) C(2,5) C(2,6) C(1,6) C(1,7) C(1,8) C(2,8) C(2,7)...
      C(3,7) C(3,8) C(4,8) C(4,7) C(4,6) C(3,6) C(3,5) C(4,5) C(5,5) C(6,5) C(6,6) C(5,6)...
      C(5,7) C(5,8) C(6,8) C(6,7) C(7,7) C(7,8) C(8,8) C(8,7) C(8,6) C(7,6) C(7,5) C(8,5)...
      C(8,4) C(8,3) C(7,3) C(7,4) C(6,4) C(5,4) C(5,3) C(6,3) C(6,2) C(5,2) C(5,1) C(6,1)...
      C(7,1) C(7,2) C(8,2) C(8,1)];

И это работает и работает быстро. Я сделал те же функции для кривых 8- и 9-го порядка, но они работают очень-очень медленно. 9-й порядок, пожалуй, никогда не закончится. По крайней мере, у меня не хватило терпения ждать конца - через 2 часа я просто выключил программу. Но кривая 7-го порядка работает в течение 15 секунд. В чем дело? Могу ли я сделать то же самое, но быстрее? Да, программе необходимо прочитать 512 * 512 элементов массива, но не может быть невозможным сделать это быстрее.

Итак, что именно мне нужно - у меня есть координаты элементов массива, и они расположены в том порядке, в котором должны быть прочитаны. Мне нужно за приемлемое время их прочитать и записать в новый массив. Как это сделать?

ps английский для меня все еще труден, если что-то неясно - спросите меня, пожалуйста.

Answer 1

Делая быстрый поиск в Интернете, вы можете найти пост о кривых Гильберта в блоге Стива Эддинса. Вот его реализация для генерации кривой:

function [x,y] = hilbert_curve(order)
    A = zeros(0,2);
    B = zeros(0,2);
    C = zeros(0,2);
    D = zeros(0,2);

    north = [ 0  1];
    east  = [ 1  0];
    south = [ 0 -1];
    west  = [-1  0];

    for i=1:order
        AA = [B ; north ; A ; east  ; A ; south ; C];
        BB = [A ; east  ; B ; north ; B ; west  ; D];
        CC = [D ; west  ; C ; south ; C ; east  ; A];
        DD = [C ; south ; D ; west  ; D ; north ; B];

        A = AA;
        B = BB;
        C = CC;
        D = DD;
    end

    subs = [0 0; cumsum(A)] + 1;
    x = subs(:,1);
    y = subs(:,2);
end

Возвращенные координаты xy являются целыми числами в диапазоне [1,2^order], Как вы можете видеть ниже, функция достаточно быстрая:

>> for order=1:10, tic, [x,y] = hilbert_curve(order); toc; end
Elapsed time is 0.001478 seconds.
Elapsed time is 0.000603 seconds.
Elapsed time is 0.000228 seconds.
Elapsed time is 0.000251 seconds.
Elapsed time is 0.000361 seconds.
Elapsed time is 0.000623 seconds.
Elapsed time is 0.001288 seconds.
Elapsed time is 0.007269 seconds.
Elapsed time is 0.029440 seconds.
Elapsed time is 0.117728 seconds.

Теперь давайте проверим это с изображением с наложенной кривой. Мы уменьшаем размер изображения до 128x128, чтобы мы могли видеть шаблон без переполненности, но вы определенно можете сделать 512x512 для своего случая:

%// some grayscale square image
img = imread('cameraman.tif');

%// scale it down for better visualization
N = 128
assert(N > 0 && mod(N,2)==0);
img = imresize(img, [N N]);

%// space-filling Hilbert curve
order = log2(N)
[x,y] = hilbert_curve(order);

%// show image with curve overlayed
imshow(img, 'InitialMagnification',400)
h = line(x, y);

Давайте немного увеличим масштаб, чтобы лучше увидеть, как кривая покрывает все пиксели:

>> zoom(10)
>> set(h, 'Marker','.')

Наконец, вы можете использовать индексы для индексации в матрице изображений:

>> ind = sub2ind([N N], x, y);
>> pix = img(ind);    %// linear indexing

где:

>> whos ind
  Name          Size             Bytes  Class     Attributes

  ind       16384x1             131072  double