FindFit для неявных функций - mathematica

Question

Я хотел бы поместить некоторые тестовые данные в какую-то неявную функцию.

Я хотел бы подогнать несколько параметров к эллиптическому уравнению f(x,y)=a, где a - известная переменная. Мои тестовые данные и функция более сложны, однако я получил больше точек данных, чем переменных. Отчасти невозможно преобразовать уравнение, которое я хочу вписать, в явную форму, такую ​​как f(x)=y. Поэтому я приложил некоторый код, чтобы получить основную идею.

Test = {{0, 1}, {0.1, 0.9}, {1.1, 0}};

Ftest = a*x^2 + b*y^2

FindFit[Test, Ftest == 2, {a, b}, {x, y}];

Однако это приводит к ошибке: количество координат (1) не равно количеству переменных \ (2). >>

Answer 1

Вы можете представить это как минимизацию наименьших квадратов:

data = {{0, 1}, {0.1, 0.9}, {1.1, 0}}
Ftest[x_, y_] := a*x^2 + b*y^2
fit = FindMinimum[ Total[(Ftest @@@ data - 2)^2] , {a, b}] 
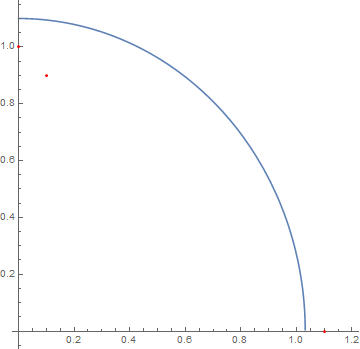
ContourPlot[ (Ftest[x, y] /. fit[[2]]) == 2 , {x, 0, 1.5}, {y, 0, 
  1.5}, Epilog -> {Red, Point /@ data}]

чтобы использовать функции подгонки, которые нужно решить для y, вы получите:

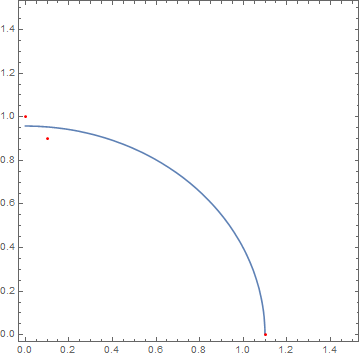
fit = NonlinearModelFit[data, Sqrt[2 - a*x^2]/Sqrt[b], {a, b}, x]

Plot[fit[x], {x, 0, 1.2}, Epilog -> {Red, Point /@ data}, 
 AspectRatio -> 1]