Интерполяция изображения из случайных пикселей
Я хотел бы задать вопрос относительно одноканальной интерполяции изображения. Один канал выбран просто для простоты, иначе я работаю над многоканальными изображениями. Предположим, что есть одноканальное изображение с чисто черным фоном (интенсивность пикселей 0), на котором есть несколько пикселей с ненулевыми значениями интенсивности. Я хочу применить алгоритм интерполяции, чтобы заполнить всю черную область изображения интерполированными значениями, поступающими из соседних пикселей с ненулевой интенсивностью.
Какой алгоритм интерполяции вы бы порекомендовали для гладкой интерполяции, применимой к этой проблеме?
В качестве входных данных мы, конечно, знаем местоположение этих не черных пикселей и их интенсивность. Но расположение несколько случайное (в одной строке может быть 10 пикселей, в другой строке только 8).

5 ответов
Регулярный interp2 здесь не будет работать, так как ваши точки не расположены через равные промежутки времени (не сидя на сетке). Вы можете попробовать TriScatteredInterp или скачать inpaint_nans из обмена файлами.
Вот решение в вашем случае с TriScatteredInterp:
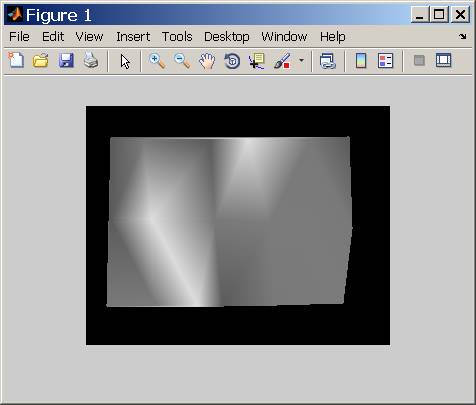
function solveStackruProblem()
im = imread('https://stackru.com/images/3ec85b9c75a3d33323aec678951ab72380b80489.png');
im = im(:,:,2);
[i,j] = find(im);
y = j; x = i;
indexes = sub2ind(size(im),i,j);
interpolator = TriScatteredInterp(x,y,double(im(indexes)));
[Y,X] = meshgrid( 1:size(im,2),1:size(im,1));
reconstructedImage = interpolator(X,Y);
figure;imshow(reconstructedImage/255)
end
Ваше лучшее решение - использовать gridfit. Он предназначен для улучшения всех собственных функций Matlab, таких как TriScatteredInterp и griddata.
Вот решение, основанное на использовании радиальных базисных функций (в данном случае гауссовых) для построения интерполяций для случайно расположенных точек с различной интенсивностью.
По сути, это отбрасывает гауссиан в каждой точке, взвешивает ее по интенсивности точки и суммирует результат.
Точность интерполяционной функции контролируется стандартным отклонением выбранной функции Гаусса.
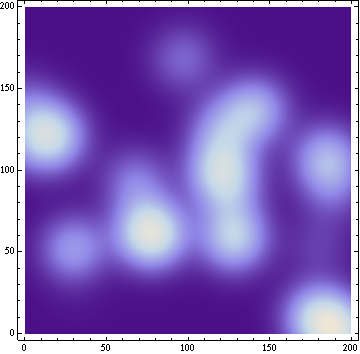
Точки:

Интерполяция:
Просмотр в 3D: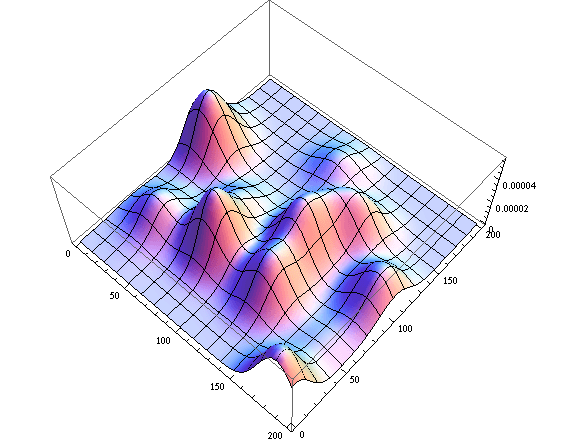
С меньшим стандартным отклонением: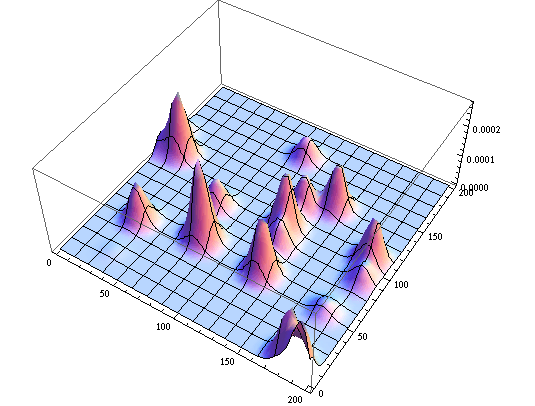
Код:
pts = Table[{{RandomReal[{0, 200}], RandomReal[{0, 200}]},
RandomReal[]}, {20}]
dists = Function[points,
Plus @@ ((PDF[
MultinormalDistribution[#, 200 IdentityMatrix[2]], {x,
y}] & /@ points[[All, 1]] ) points[[All, 2]])/Length@points]
DensityPlot[dists[pts], {x, 0, 200}, {y, 0, 200}, PlotPoints -> 100]
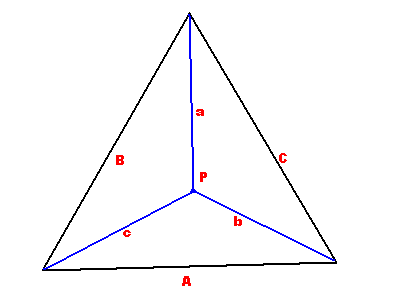
Для относительно небольшого числа точек идеальным способом их интерполяции было бы создание треугольной сетки, используя только вершины каждой области для определения пикселей в этой области, используя взвешенное среднее значение для определения цвета каждого пикселя.
Чтобы найти цвет пикселя внутри треугольной области, весовые коэффициенты, которые необходимо использовать для каждого пикселя, для точек A, B и C соответственно (bc-A)/ a, (a cB)/b и (а * до Р.Х.)/ с. Это гарантирует, что влияние каждой точки уменьшается до нуля, когда точка приближается к противоположному краю, так что переходы между треугольниками являются плавными.
Имейте в виду, что для расчета можно использовать любое среднее значение, в том числе гармоническое и геометрическое, а не только арифметическое (внешний вид изменится, но в любом случае другие типы средств могут быть лучше).
Любая интерполяция будет выглядеть очень плохо с этими несколькими ненулевыми точками, но вы можете попробовать свертить изображение с помощью двумерного фильтра, такого как ядро Гаусса, и посмотреть, понравится ли вам это.