Подходящие распределения, качество посадки, p-значение. Возможно ли это сделать с помощью Scipy (Python)?
ВВЕДЕНИЕ: Я биоинформатик. В моем анализе, который я выполняю для всех человеческих генов (около 20 000), я ищу определенный мотив короткой последовательности, чтобы проверить, сколько раз этот мотив встречается в каждом гене.
Гены "записаны" в линейной последовательности из четырех букв (A,T,G,C). Например: CGTAGGGGGTTTAC... Это четырехбуквенный алфавит генетического кода, который похож на секретный язык каждой клетки, именно так ДНК хранит информацию.
Я подозреваю, что частые повторения определенной короткой мотивной последовательности (AGTGGAC) в некоторых генах имеют решающее значение в специфическом биохимическом процессе в клетке. Поскольку сам мотив очень короткий, с помощью вычислительных инструментов трудно различить истинные функциональные примеры в генах и те, которые выглядят случайно. Чтобы избежать этой проблемы, я получаю последовательности всех генов и объединяю их в одну строку и перемешиваю. Длина каждого из исходных генов была сохранена. Затем для каждой из исходных длин последовательностей была построена случайная последовательность путем многократного выбора A или T или G или C случайным образом из объединенной последовательности и передачи ее в случайную последовательность. Таким образом, результирующий набор рандомизированных последовательностей имеет такое же распределение длины, как и общий состав A, T, G, C. Затем я ищу мотив в этих рандомизированных последовательностях. Я выполнил эту процедуру 1000 раз и усреднил результаты.
15000 генов, которые не содержат данный мотив 5000 генов, которые содержат 1 мотив 3000 генов, которые содержат 2 мотива 1000 генов, которые содержат 3 мотива... 1 ген, который содержит 6 мотивов
Таким образом, даже после 1000-кратной рандомизации истинного генетического кода нет никаких генов, которые бы имели более 6 мотивов. Но в истинном генетическом коде есть несколько генов, которые содержат более 20 вхождений мотива, что говорит о том, что эти повторения могут быть функциональными, и вряд ли их можно найти в таком изобилии по чистой случайности.
ПРОБЛЕМА: Я хотел бы знать вероятность обнаружения гена, скажем, с 20 случаями мотива в моем распределении. Поэтому я хочу знать вероятность случайного нахождения такого гена. Я хотел бы реализовать это в Python, но я не знаю как.
Могу ли я сделать такой анализ в Python?
Любая помощь будет оценена.
2 ответа
В документации SciPy вы найдете список всех реализованных функций непрерывного распределения. У каждого есть fit() метод, который возвращает соответствующие параметры формы.
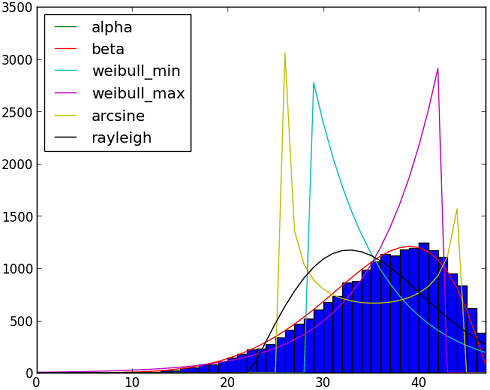
Даже если вы не знаете, какой дистрибутив использовать, вы можете попробовать несколько дистрибутивов одновременно и выбрать тот, который лучше соответствует вашим данным, как показано в коде ниже. Обратите внимание, что если вы не имеете представления о распределении, может быть сложно подобрать образец.
import matplotlib.pyplot as plt
import scipy
import scipy.stats
size = 20000
x = scipy.arange(size)
# creating the dummy sample (using beta distribution)
y = scipy.int_(scipy.round_(scipy.stats.beta.rvs(6,2,size=size)*47))
# creating the histogram
h = plt.hist(y, bins=range(48))
dist_names = ['alpha', 'beta', 'arcsine',
'weibull_min', 'weibull_max', 'rayleigh']
for dist_name in dist_names:
dist = getattr(scipy.stats, dist_name)
param = dist.fit(y)
pdf_fitted = dist.pdf(x, *param[:-2], loc=param[-2], scale=param[-1]) * size
plt.plot(pdf_fitted, label=dist_name)
plt.xlim(0,47)
plt.legend(loc='upper left')
plt.show()
Рекомендации:
- Распределительная арматура со Scipy
- Подгонка эмпирического распределения к теоретическим с помощью Scipy (Python)?
import numpy as np
import pandas as pd
import scipy.stats as st
import statsmodels.api as sm
import matplotlib as mpl
import matplotlib.pyplot as plt
import math
import random
mpl.style.use("ggplot")
def danoes_formula(data):
"""
DANOE'S FORMULA
https://en.wikipedia.org/wiki/Histogram#Doane's_formula
"""
N = len(data)
skewness = st.skew(data)
sigma_g1 = math.sqrt((6*(N-2))/((N+1)*(N+3)))
num_bins = 1 + math.log(N,2) + math.log(1+abs(skewness)/sigma_g1,2)
num_bins = round(num_bins)
return num_bins
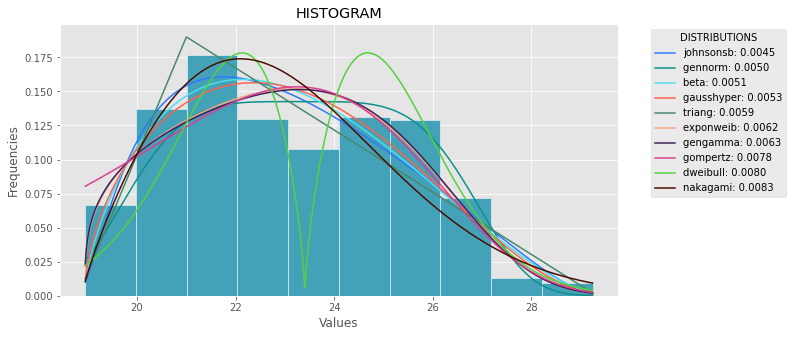
def plot_histogram(data, results, n):
## n first distribution of the ranking
N_DISTRIBUTIONS = {k: results[k] for k in list(results)[:n]}
## Histogram of data
plt.figure(figsize=(10, 5))
plt.hist(data, density=True, ec='white', color=(63/235, 149/235, 170/235))
plt.title('HISTOGRAM')
plt.xlabel('Values')
plt.ylabel('Frequencies')
## Plot n distributions
for i, distribution in N_DISTRIBUTIONS:
sse = results[distribution][0]
arg = results[distribution][1]
loc = results[distribution][2]
scale = results[distribution][3]
x_plot = np.linspace(min(data), max(data), 1000)
y_plot = distribution.pdf(x_plot, loc=loc, scale=scale, *arg)
plt.plot(x_plot, y_plot, label=str(distribution)[32:-34] + ": " + str(sse)[0:6], color=(random.uniform(0, 1), random.uniform(0, 1), random.uniform(0, 1)))
plt.legend(title='DISTRIBUTIONS', bbox_to_anchor=(1.05, 1), loc='upper left')
plt.show()
def fit_data(data):
## st.frechet_r,st.frechet_l: are disbled in current SciPy version
## st.levy_stable: a lot of time of estimation parameters
DISTRIBUTIONS = [
st.alpha,st.anglit,st.arcsine,st.beta,st.betaprime,st.bradford,st.burr,st.cauchy,st.chi,st.chi2,st.cosine,
st.dgamma,st.dweibull,st.erlang,st.expon,st.exponnorm,st.exponweib,st.exponpow,st.f,st.fatiguelife,st.fisk,
st.foldcauchy,st.foldnorm, st.genlogistic,st.genpareto,st.gennorm,st.genexpon,
st.genextreme,st.gausshyper,st.gamma,st.gengamma,st.genhalflogistic,st.gilbrat,st.gompertz,st.gumbel_r,
st.gumbel_l,st.halfcauchy,st.halflogistic,st.halfnorm,st.halfgennorm,st.hypsecant,st.invgamma,st.invgauss,
st.invweibull,st.johnsonsb,st.johnsonsu,st.ksone,st.kstwobign,st.laplace,st.levy,st.levy_l,
st.logistic,st.loggamma,st.loglaplace,st.lognorm,st.lomax,st.maxwell,st.mielke,st.nakagami,st.ncx2,st.ncf,
st.nct,st.norm,st.pareto,st.pearson3,st.powerlaw,st.powerlognorm,st.powernorm,st.rdist,st.reciprocal,
st.rayleigh,st.rice,st.recipinvgauss,st.semicircular,st.t,st.triang,st.truncexpon,st.truncnorm,st.tukeylambda,
st.uniform,st.vonmises,st.vonmises_line,st.wald,st.weibull_min,st.weibull_max,st.wrapcauchy
]
## Calculae Histogram
num_bins = danoes_formula(data)
frequencies, bin_edges = np.histogram(data, num_bins, density=True)
central_values = [(bin_edges[i] + bin_edges[i+1])/2 for i in range(len(bin_edges)-1)]
results = {}
for distribution in DISTRIBUTIONS:
## Get parameters of distribution
params = distribution.fit(data)
## Separate parts of parameters
arg = params[:-2]
loc = params[-2]
scale = params[-1]
## Calculate fitted PDF and error with fit in distribution
pdf_values = [distribution.pdf(c, loc=loc, scale=scale, *arg) for c in central_values]
## Calculate SSE (sum of squared estimate of errors)
sse = np.sum(np.power(frequencies - pdf_values, 2.0))
## Build results and sort by sse
results[distribution] = [sse, arg, loc, scale]
results = {k: results[k] for k in sorted(results, key=results.get)}
return results
def main():
## Import data
data = pd.Series(sm.datasets.elnino.load_pandas().data.set_index('YEAR').values.ravel())
results = fit_data(data)
plot_histogram(data, results, 10)
if __name__ == "__main__":
main()